주성분 분석
고차원의 데이터를 저차원의 데이터로 환원시키는 기법 중 하나 (차원 축소) -wikipedia-
서로 연관 가능성이 있는 고차원 피처들을 선형 연관성이 없는 피처로 변환하기 위해 직교 변환을 사용. 이러한 직교 변환을 수행할 때 원 데이터의 표현력을 '잘' 보존하기 위해 주성분 분석의 핵심인 분산(Variance)을 최대로 하는 주축을 찾아야 한다.
여기서 분산이란 데이터가 퍼진 정도를 의미한다. 만약 2차원 공간이 있고 1차원 공간으로 차원 축소 한다면 1차원 공간상에서 데이터 분포가 가장 넓게 퍼지게 만드는 벡터를 찾아야 한다.[예시]
왼쪽에 있는 2차원 데이터를 오른쪽에 있는 1차원 데이터로 차원 축소를 한다면 어떻게 해야 원 데이터의 성질을 잘 반영할까?
- 차원축소는 왜 필요할까?
-고차원으로 표현된 데이터는 계산 비용 많고 분석에 필요한 시각화 문제.
-고차원을 이루는 피처 중 상대적으로 중요도가 낮은 피처를 제외하는 대신 계산 비용이나 비교적 준수한 성능 선택.
참고: PCA에서 가장 큰 분산이 되는 축을 설정하는 이유
-
데이터 변동성 최대화
가장 큰 분산을 가지는 축(주성분)은 데이터의 변동성을 최대한 많이 포착하는 방향을 나타내며 이는 데이터를 저차원으로 투영할 때 중요한 정보를 최대한 유지. -
정보 손실 최소화
-
데이터의 주요 패턴 파악
-
차원 축소와 노이즈 감소
위에서 말한대로 2차원 공간을 1차원으로 줄일 때 2차원에 넓게 퍼진 데이터 분포를 1차원 상에서도 똑같이 넓게 퍼질 수 있도록 하는 "벡터"를 찾아야 한다. 여기서 "벡터"는 곧 주축 (= '고유 벡터')을 의미한다. 피처들을 고유벡터에 사상시킬 때 분산이 최대가 되는 주성분이 만들어진다. 이렇게 분산이 가장 큰 주성분을 첫 번째 주성분, 두 번째로 큰 축을 두 번째 주성분이라 한다.
다음 아래 그림으로 이해해보자.

-
단위 원을 이루는 벡터(왼쪽)를 행렬을 이용한 선형변환을 통해 1,3사분면으로 넓게 퍼지는 벡터(오른쪽)로 변환.
-
변환된 벡터들 중 빨간색으로 표시된 벡터 2개만은 변환 전과 후의 방향이 동일.
-
빨간 두개의 벡터가 고유벡터이며, 이때 변환 전과 후의 길이 변화 비율을 고윳값이라고 한다.
-
차원의 데이터에는 개의 고유벡터, 고윳값이 존재하는데 가장 큰 고윳값이 데이터를 가장 잘 설명해주는 주축이 된다.
-
피처들을 고유벡터에 사상시켜 주성분을 만든다.
-
약 80 ~ 90%의 데이터를 설명할 수 있을 때 까지 주성분을 추가해준다.
그렇다면 이 주축인 고유 벡터는 어떻게 구하고, 고유 벡터에 피처를 어떻게 사상시킬수 있는 것일까?
고유 벡터를 구하기 위해서는 특이값 분해 (SVD, Singular Value Decomposition)가 수행되고 사상을 위해서 공분산 행렬이 필요하다.
즉, 데이터들의 공분산 행렬에 대한 특이값 분해(SVD)로 볼 수 있다.
공분산 행렬
두 변수의 변동이 얼마나 닮았는가(다른 말로는 얼마만큼이나 함께 변하는가)를 행렬로 표현.
기하학적 의미
행렬이란 선형 변환 (사상)이고 하나의 벡터 공간을 선형적으로 다른 벡터 공간으로 mapping 하는 기능을 가진다.
즉, 공간상에 한 벡터가 있을 때 공분산 행렬을 곱해주게 되면 그 벡터의 선형 변환이 이루어진다.
주성분 분석에서는 기하학적 의미로 활용된다.
즉 공분산 행렬엔 변수간 공변 정보가 담겨 있으므로 이를 주축인 고유벡터에 사상시키면 주성분을 구할 수 있다.
행렬 가 차원에 있을 때 (예; 명의 사람들로부터 각각 개의 특징(feature) 추출)
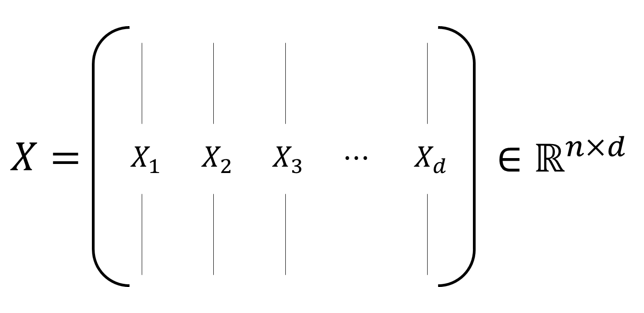
라고 정의하고
행렬 의 공분산 행렬을 구하기 위해선 앞에 를 곱해준다.
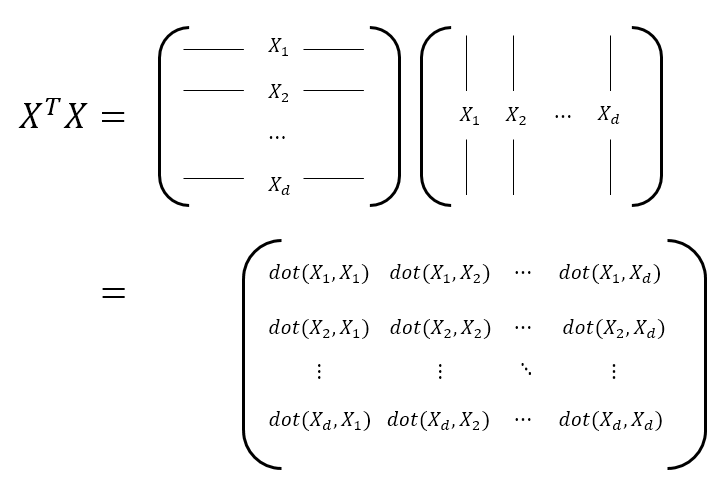
그렇다면 의미는 무엇인가?
의 행 열의 성분인 (는 개의 feature 중 번째 feature와 번째 feature가 얼마나 닮았는지를 모든 사람으로부터 값을 얻어서 내적 연산을 취함으로써 확인시켜준다.
이 행렬에서 모든 대각 성분은 같은 피처 간 내적이므로 분산에 해당하고 대각 성분 이외에는 모두 다른 피처 간 내적이므로 공분산에 해당한다.
예시
일 때
그런데 행렬은 이 커질수록 내적 값은 계속 커진다는 것이다. 이를 방지하기 위해서는 내적값들을 으로 나눠주어 해결.
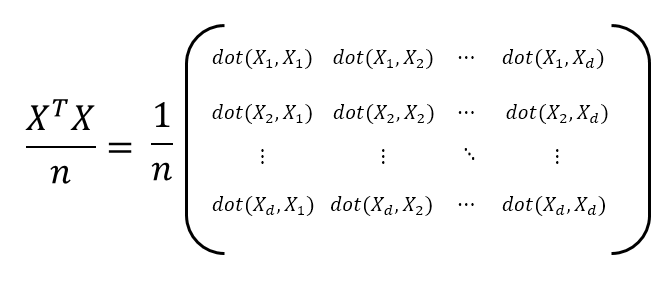
으로 나눈 행렬을 공분산 행렬이라고 부른다.
즉, 데이터 행렬 에 대해서 공분산행렬 는
가 된다.
위에서 계속 진행하던 예시 데이터에서 공분산 행렬을 계산해보면 다음과 같다.
고유벡터와 고윳값
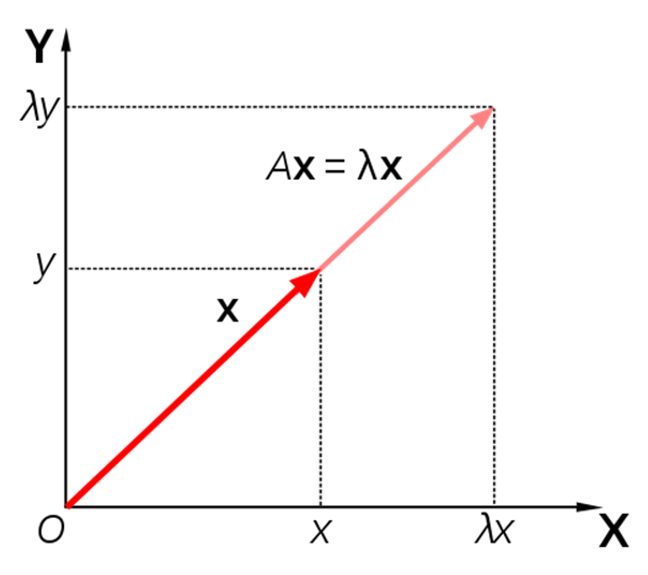
임의의 행렬 에 대하여, 0이 아닌 벡터 가 존재한다면 숫자 는 행렬 의 고윳값라고 할 수 있으며 이 때 는 고유벡터이다.
이 때, 위 식은
으로 바꿀 수 있다. 는 identity matrix이다.
괄호안에 있는 식으로 부터 얻는 행렬은 역행렬을 가지지 않아야만 해를 구할 수 있다. 따라서 다음을 만족해야 한다.
참고
벡터에 행렬 연산을 취해주면 원래 것과 다른 벡터가 나온다는 것이었다. 그런데, 특정한 벡터와 행렬은 선형 변환을 취해주었을 때, 크기만 바뀌고 방향은 바뀌지 않을 수도 있다.
예를 들어, 변환 전의 벡터()에는
을 입력으로 넣어주고, matrix에는
를 입력하면 방향은 같고 크기만 다른 벡터가 생성된다.
즉, 입력 벡터 를 로 선형변환 시킨 결과()가 상수배라는 것이다.
예시
다음과 같은 행렬 A를 생각해보자.
이 행렬에 대해 고윳값과 고유벡터를 구해보도록 하자.
행렬의 성질에 의해
이다. 또한, 가 nontrivial solution을 갖기 위해서는 다음이 만족해야 한다.
그러므로,
선형변환 의 고윳값는 1과3이다. 선형 변환을 했을 때 그 크기는 변하고 방향이 변하지 않는 벡터가 있다고 할 때, 그 벡터의 크기는 각각 1배와 3배가 된다는 의미이다. 이제, 고유벡터를 찾아보도록 하자.
다시 한번 식 (2)는 고윳값 에 대해서 모두 만족해야 한다. 그러므로,
인 경우에 대해,
를 만족해야 하므로 아래의 연립방정식이 성립되어야 한다.
그러므로, 인 경우의 고유벡터는
이며,
인 경우의 고유벡터는
그러므로 기하학적으로 이것을 다시 설명하면, 벡터는 선형변환 를 취해주면 그 방향은 변하지 않고, 크기가 3배가 된다. 또, 벡터는 선형변환 를 취해주게 되면 그 방향은 변하지 않고 크기는 1배가 된다는 의미이다.
Reference
https://ko.wikipedia.org/wiki/%EC%A3%BC%EC%84%B1%EB%B6%84_%EB%B6%84%EC%84%9D
https://roytravel.tistory.com/341
