[딥러닝] 학습 기술들

Chris Kim·2024년 11월 21일

딥러닝

목록 보기

5/5

1. 매개변수 갱신 방법

1.1 확률적 경사 하강법(SGD)

1.1.1 파이썬 클래스 구현

확률적 경사 하강법을 파이썬 클래스로 구현하면 다음과 같다.

class SGD:
	def __init__(self, lr=0.01)
    	self.lr = lr
    
    def ubdate(self, params, grads):
    	for key in params.keys():
        	params[key] -= self.lr * grads[key]

1.1.2 SGD의 단점

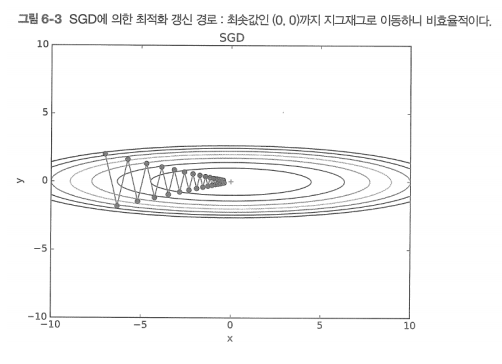
하지만 문제에 따라서 SGD가 비효율적일 수 있다. 예를 들어 다음과 같은 함수

f(x,y) = \frac{1}{20}x^2+y^2

의 경우 3차원 공간에서 bowl을 x축 방향으로 길게 늘린 모양이다. 이런 함수, 즉 비등방성(anisotropy) 함수에서는 탐색 경로가 비효율적이게 된다. 왜냐하면 임의 지점의 기울기가 최솟값의 위치를 가리키지 않기 때문이다.(이 경우 최적화 갱신경로는 지그재그로 움직이게 된다.)

1.2 모멘텀

모멘텀(momentum) 기법은 위의 SGD의 단점을 보완해준다. 모멘텀 기법은 수식으로 다음과 같이 나타낼 수 있다.

v\leftarrow\alpha v - \eta\frac{\partial L}{\partial W}\\

W \leftarrow W + v

파이썬으로는 다음과 같이 구현할 수 있다.

class Momentum:
	def __init__(self, lr=0.01, momentum=0.9):
    	self.lr = lr
        slef.momentum = momentum
        self.v = None
    
    def ubdate(self, params, grads):
    	if self.v is None:
        	self.v = {}
            for key, val in parrams.items():
            	self.v[key] = np.zeros_like(val)

			for key in params.keys():
            	self.v[key] = self.momentum*self.v[key] + self.lr*grads[key]
                params[key] += self.v[key]

이미지로 최적화 갱신 경로를 나타내면 다음과 같다.

1.3 AdaGrad

적절한 학습률의 결정은 매우 중요하다. 너무 작으면 학습시간이 길어지고, 너무 커지면 자칫 발산할 수 있기 때문이다. 따라서 학습률 감소(learning rate decay) 이란 기술을 사용하기도 한다. AdaGrad는 '각각의' 매개변수에 '맞춤형' 값을 만들어 준다.

h\leftarrow h - \frac{\partial L}{\partial W}\odot\frac{\partial L}{\partial W}\\

W\leftarrow W - \eta\frac{1}{\sqrt h}\frac{\partial L}{\partial W}

$h$ 에 기존 기울기 값을 제곱하여 계속 더해준다. 그리고 매개변수를 갱신할 떄 학습률을 조정한다. 이 식에 따르면 매개변수의 원소 중에서 많이 움직인 원소는 학습률이 낮아진다.

파이썬 클래스로는 다음과 같이 구현할 수 있다.

class AdaGrad:
	def __init__(self, lr=0.01):
    	self.lr = lr
        self.h = None
    
    def update(self, params, grads):
    	if self.h = None:
        	self.h = {}
        
        	for key, val in params.items():
            	self.h[key] = np.zeros_like(val)
        
        for key in params.keys():
        	self.h[key] += grads[key]*grads[key]
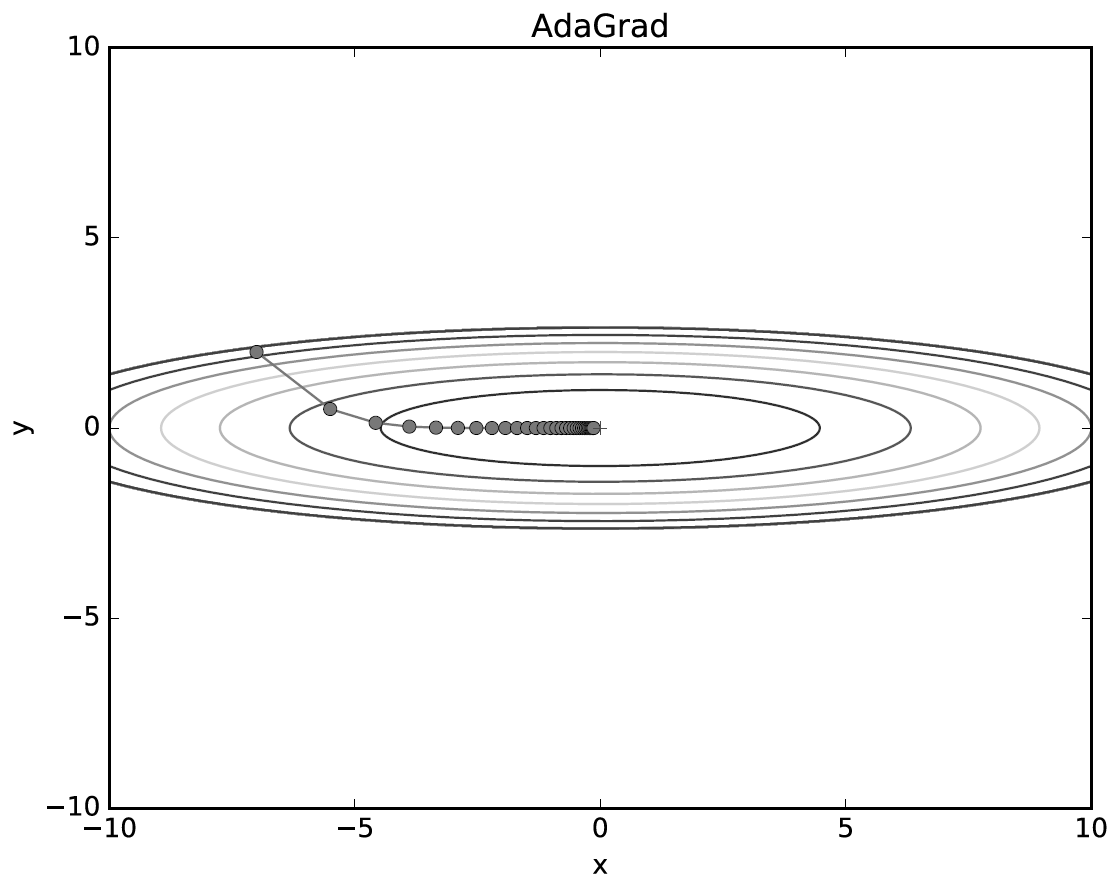
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

최적화 갱신경로는 다음과 같다.

1.4 Adam

Adam은 AdaGrad와 모멘텀, 두 기법을 융합한 방법이라고 생각하면 이해하기 쉽다. 파이썬을 통한 예시 코드는 다음과 같다.

class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
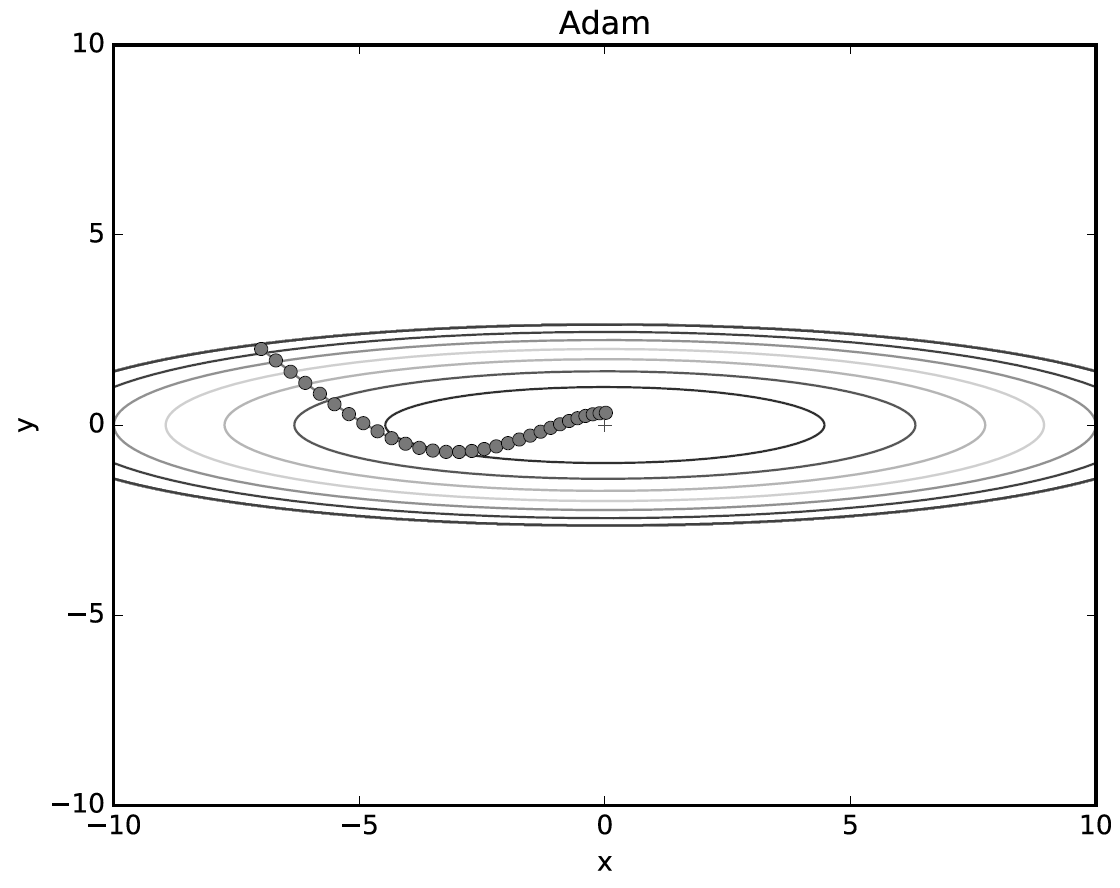
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

최적화 갱신경로는 다음과 같이 나타난다.

2. 가중치 초깃값

2.1 초깃값 0

초깃값을 모두 0으로 설정하는 경우 오차 역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문이다. 즉 순전파의 결과가 모두 같아지기 떄문에 역전파에 의한 가중치 갱신도 똑같이 이뤄진다는 뜻이다. 이를 막기위해 초깃값은 무작위로 설정되어야 한다.(ex. np.random.randn(10,100))

2.2 은닉층의 활성화값 분포

2.2.1 Xavier 초깃값

시그모이드 함수가 사용될 때, 표준편차가 너무 크면 기울기 소실이, 너무 작으면 활성화 값이 치우쳐져 표현력이 제한된다. 이에 사비에르 그로로트와 요슈아 벤지오는 앞 계층의 노드가 $n$ 개인 경우, 표준편차가 $\frac{1}{\sqrt n}$ 인 분포를 사용하면 된다는 결론을 이끌어 냈다. 이를 Xavier 초깃값이라고 한다.

2.2.2 He 초깃값

ReLU는 시그모이드 함수와 달리 좌우 대칭의 함수가 아니다. 따라서 이에 특화된 초깃값을 사용해야하는데 바로 He 초깃값 이다.
He 초깃값은 앞 계층의 노드가 $n$ 개인 경우, 표준편차가 $\sqrt\frac{2}{n}$ 인 정규분포를 사용한다. Xavier 초깃값보다 표준편차가 두 배인데, 음의 영역이 0이므로 더 넓은 분포를 위해 두 배의 계수를 사용한다고 이해하면 편하다.

3. 배치 정규화

3.1 배치 정규화 알고리즘

배치 정규화는 2015년에 제안된 방법으로 다음과 같은 이점을 가진다.

학습 속도 개선
초깃값 의존성 감소
오버피팅 억제

배치 정규화는 그 이름과 같이 학습 시 미니배치를 단위로 정규화한다. 구체적으로는 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화 한다. 수식으로는 다음과 같이 표현할 수 있다.

\mu \leftarrow \frac{1}{m}\sum\limits_{i=1}^m x_i

\sigma^2_B \leftarrow \frac{1}{m}\sum\limits_{i=1}^m (x_i-\mu_B)^2

\hat{x}_i \leftarrow \frac{(x_i-\mu_B)^2}{\sqrt {o^2_B+\epsilon}}

배치 정규화 처리를 활성화 앞 혹은 뒤에 삽입 함으로써 데이터 분포가 덜 치우치게 할 수 있다. 또, 배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대와 이동 변환을 수행한다. 수식으로는 다음과 같이 표현할 수 있다.

y_i \leftarrow \gamma\hat{x}_i+\beta

4. 가중치 감소, 드롭아웃

4.1 오버피팅

훈련 데이터에 치우쳐 적응하는 경우, 훈련 데이터의 정확성과 시험 데이터의 정확성 간의 괴리가 커진다. 이는 곧 범용성이 낮아짐을 의미한다. 따라서 반드시 이를 해결해야만 한다.

4.2 가중치 감소

오래전부터 가중치 감소(weight decay) 는 오버피팅을 억제하기 위해 많이 사용되었다. 왜냐하면 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문이다. 가중치 감소는 모든 가중치 각각의 손실 함수에 $\frac{1}{2} \lambda W^2$ 을 더하는 방식으로 이뤄지며 가중치의 기울기를 구하는 계산에서는 정규화 항을 미분한 $\lambda W$ 를 더한다.

4.3 드롭아웃

신경망 모델이 복잡해지면 가중치 감소만으로는 대응하기 어려워진다. 이럴 때는 드롭아웃(Dropout) 이라는 기법을 이용한다. 드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법으로 훈련을 할 때, 은닉층의 뉴런을 무작위로 골라 삭제한다. 파이썬으로는 다음과 같이 구현할 수 있다.

class Dropout: 
	def __init__(self, dropout_ratio=0.5):
    	self.dropout_ratio = dropout_ratio
        sel.mask = None
    
    def forward(self, x, train_flg=True):
    	if train_flg:
        	self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
        	return x * (1.0 - self.dropout_ratio)
    
    def backward(self, dout):
    	return dout * self.mask

5. 하이퍼파라미터 탐색

5.1 검증 데이터

하이퍼파라미터 또한 평가의 대상이 될 수 있다. 여기서 주의할 점은 하이퍼파라미터의 성능을 평가할 때, 시험 데이터를 사용해서는 안된다는 것이다. 왜냐하면 시험 데이터를 사용해서 하이퍼파라미터를 조정하면 하이퍼파라미터 값이 시험 데이터에 오버피팅되기 때문이다. 따라서 하이퍼파라미터 전용 확인 데이터가 필요하다. 이 조정용 데이터를 일반적으로 검증 데이터라고 부른다.
검증 데이터가 미리 분리되어 있는 경우도 있지만, 없는 경우에 가장 간단한 방법은 훈련 데이터 중 20% 정도를 검증 데이터로 먼저 분리하는 것이다.

5.2 하이퍼파라미터 최적화

하이퍼파라미터 최적화의 핵심은 최적 값이 존재하는 범위를 조금씩 줄여나가는 것이다. 일반적으로 범위는 '로그 스케일'로 지정한다. 그리고 검증 데이터로 정확도를 반복적으로 평가한 뒤, 결과를 보고 하이퍼파라미터의 범위를 좁힌다. 그리고 이 과정을 반복적으로 수행하고 최종 하이퍼파라미터 값을 하나 선택한다.

Chris Kim

회계+IT=???

이전 포스트