StyleGAN-1

Introduction

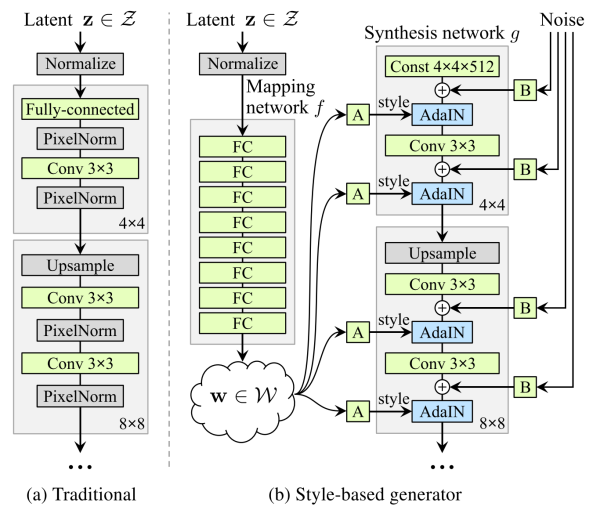
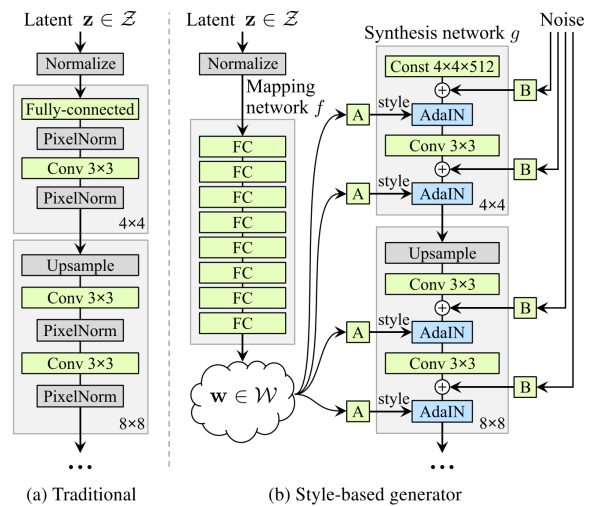
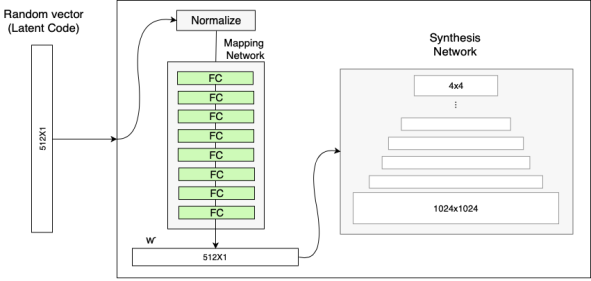
StyleGAN synthesizes images through the use of affine transformation from z to some other space w, and then using the "style" information as an input to the AdaIN layer. The biggest difference between StyleGAN with other gans is that stylegan generates image from the warped distribution, w, instead of directly generating image from the initial distribution, z.

Model Structure

The structure of stylegan is as the following.

AdaIN layer's operation is defined by:

$AdaIN(x_i, y) = y_{s,i} * norm(x_i, mu_x, sigma_y) + y_{b,i}$ ,
where $y=(y_s,y_b)$ is the style input and x is the input to the layer.

In essence the AdaIN layer is normalizing the statistics of inputs and outputs to the convolution layer, and feeding the statistics of the style input. This way we can keep the information of x while transforming the distribution of the output of AdaIN to be similar to the style input.

The synthesis network uses progressive gan structure as its backbone, where the network grows from low resolution to high resolution as training continues. In other words, the network starts with a single layer of 4x4 resolution block, as it saturates, grows to 8x8, ... until it reaches the expected output size.

Stochastic Variation

Noise is given as an input to each synthesis block in order to capture variational details and thus rendering the image to be seen more realistic. Furthermore, the input latent vector can focus on "important features" such as gender, ethnicity and hairstyle. This leads to more controllability of the input style vector.

Style Mixing

The intermediate vector w is used on all the synthesis block layers during training. This might lead to style being correlated on multiple layers; i.e. when trying to merge "style" information we give different style input to different layers, but if trained without style mixing it causes the different style inputs to be correlated to each other.

Style mixing is a technique to overcome this issue. When training, we create $w_1, w_2$ from two input vectors. At the start of the training the network is trained with $w_1$. After a certain layer $w_2$ is applied. Now assign the layers to which the style mixing happens in the network randomly, in order to prevent the style being correlated.

Inference

The biggest question to me in stylegan was how the inference happens. It is actually very simple, and crude in my opinion.

First of all you generate images to be used as base image and style image from latent code, z. After knowing which z's to mix, you decide on which "resolution" layer you will dedicate the style image to. When the style input is given as an input for the low resolution blocks, you will have some coarse style inputs such as color, hair style etc.

Evaluation Metric

Perceptual path length

In short, this metric measures how drastic changes the image undergoes as interpolation in the latent space takes place. Less drastic the change is, the better (less entangled latent space).

Perceptual path length used in this paper uses VGG16 embeddings, and measures the changes through perceptual distance between the two resulting images (two images are sent through VGG16, and the distance is measured between the two).

$l_Z = E[1/e^2*d(G(slerp(z_1,z_2;t)), G(slerp(z_1,z_2;t+e)))]$

where $z_1,z_2~P(z),t~U(0,1)$, G is the generator, and $d( , )$ evaluates the perceptual distance.

Here, the scale constant, t, signifies how much a step in the interpolation trajectory we are going to count. By adding some noise e as a constant in the latter term, the expectation above is essentially finding the expected perceptual distance between the generated samples from slightly different steps we take in the z space trajectory.

The paper uses slerp for z, and lerp for w, since z is normalized and w has no operation related to normalization. Therefore, z space should be close to spherical and w space should be close to linear.