다이나믹 프로그래밍
❓다이나믹 프로그래밍(DP)이란?
여러 개의 하위문제를 푼 후, 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘이다.
DP로 풀 수 있는 문제는 다음과 같은 조건을 만족시킨다.
1. 최적 부분 구조
- dp[1, 2, .... i-1]로 dp[i]가 도출될 수 있어야 한다.
2. 겹치는 부분 문제
- 문제를 작은 문제로 쪼갤 수 있어야 한다.
- 큰 문제와 작은 문제를 같은 방법으로 풀 수 있어야 한다.
분명 한글로 쓰고 있는데 뭔 소린지 모르겠다.

진정하고 fibo(5)를 트리 구조로 그리면서 이해해보자.
int fibo(int n) {
if(n<=1) return 1;
return fibo(n-2)+fibo(n-1);
}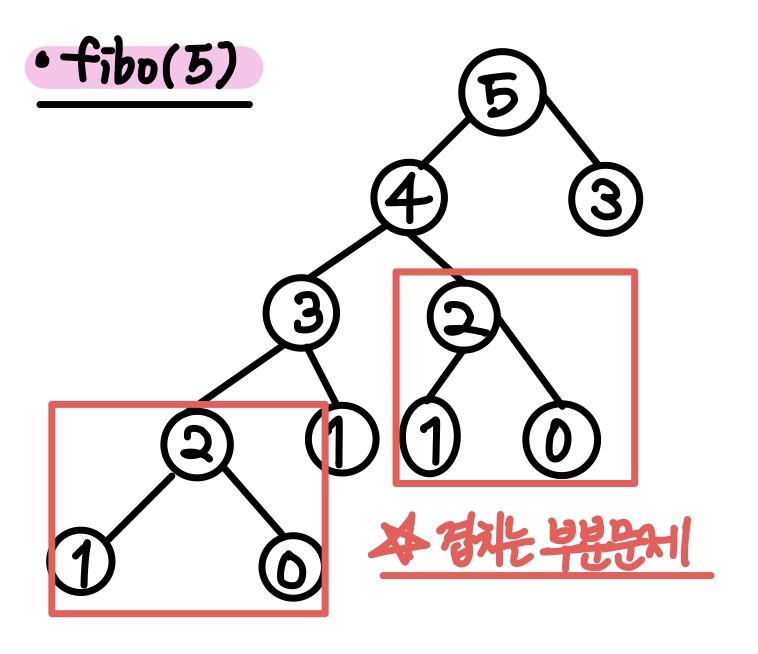
아! 그려보니까 감이 좀 잡힌다.
피보나치 수열을 재귀호출로 풀면, fibo(2)를 계속 호출해야 한다는 '겹치는 부분문제'가 계속 생기니까 커다란 낭비가 생긴다.
그래서 기억이 날락말락한 게, 자료구조 수업시간에 교수님께서 피보나치 수열을 코드로 짤 때 recursion VS iteration 이슈에서 recursion으로 풀면 굉장히 비효율적이기 때문에 iteration으로 푸는 게 낫다라는 말씀을 잠결에 들은 것 같다.
💡 DP는 '메모하면서 풀기'이다.
그렇다면 피보나치 수열을 좀 더 똑똑하게 풀 수 있는 방법은 없을까?
딱 봐도 fibo(2) 을 낭비 없이, 한 번만 호출하고도 풀 수 있는 방법은 해당 값(fibo(2))을 기억+저장(메모이제이션, 캐싱)하면서 푸는 것이 있을 것이다.
피보나치 수열을 DP로 풀었을 때와 아니었을 때의 함수 호출횟수를 비교하기 위한 기초적인 예제를 풀어보자.
💻 정답 코드
//동적 계획법의 기초 문제
#include <iostream>
using namespace std;
int n, cnt1=0, cnt2=0;
int dp[44]; //#1 테이블 정의하기: dp는 n항의 값을 저장하는 배열
//1. 재귀 호출 함수
int recur_fib(int n) {
if(n==1 || n==2) {
cnt1++; return 1;
}
return recur_fib(n-1)+recur_fib(n-2);
}
// 2. dp로 풀기
int dp_fib(int n) {
dp[1] = dp[2] = 1; //#3. 초기값 셋팅
for(int i = 3; i <= n; i++) {
dp[i] = dp[i-2]+dp[i-1]; //#2. 점화식 찾기
cnt2++;
}
return dp[n];
}
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
cin >> n;
recur_fib(n);
dp_fib(n);
cout << cnt1 << " " << cnt2;
}💡 DP 문제를 설계하는 과정
- STEP 1. 상태 정의 하기
: dp배열이 무엇인지 정의하여야 한다.제일 중요한 과정이자 내가 제일 못하는 과정.- STEP 2. 점화식 찾기
- STEP 3. 초기값 설정하기
문제를 직접 풀면서 이해하면 빠를 것이다.
문제 풀러 바로가기 >> 9095 :: 1,2,3 더하기
문제
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.
출력
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
🤔 내가 생각한 로직
☝️ STEP 1. 테이블을 정의한다.
DP[i] = i를 1, 2, 3의 합으로 나타내는 방법의 수
✌️ STEP 2. 점화식을 찾는다.
나 같은 비에이비오(babo)는 차근차근 해야 하므로 하나하나 다 적어보도록 하겠다.
-
DP[1]은 {1}로 나타낼 수 있으므로,DP[1]=1이다. -
DP[2]은 {1+1, 2}로 나타낼 수 있으므로,DP[2]=2이다. -
DP[3]은 {1+1+1, 2+1, 1+2, 3}으로 나타낼 수 있으므로,DP[3]=4이다. -
DP[4]은 {1+1+1+1, 2+1+1, 3+1, 1+2+1, 1+1+2, 2+2, 1+3} 으로 나타낼 수 있으므로,DP[4]=7이다.
여기서 잠깐! DP[4]를 구하면서 이상한 찝찝함+기시감이 든다. 뭔가 똑같은 노동을(?) 하고 있는 기분이...😣
그러면 잠깐 멈추고, 한번 DP[1], DP[2], DP[3], DP[4]를 구했던 과정을 바탕으로 수식을 분석하여 점화식을 도출해보자!

DP[i] = DP[i-1]+DP[i-2]+DP[i-3] (단, i>=4)
👌 STEP 3. 초기값을 셋팅한다.
점화식을 찾았으면, 초기값 셋팅은 비교적 쉽다.
아까 이끌어낸 점화식의 조건에 i>=4가 붙었으므로, i<4인 경우를 정의해주면 된다.
DP[1] = 1;
DP[2] = 2;
DP[3] = 4;
💻 정답 코드
#include <iostream>
using namespace std;
int t;
int main() {
ios_base::sync_with_stdio(false); cin.tie(0);
cin >> t;
int DP[12];
DP[1] = 1; DP[2] = 2; DP[3] = 4; //초기값 셋팅
for(int i = 4; i < 12; i++) {
DP[i] = DP[i-1] + DP[i-2] + DP[i-3];
}
while(t--){
int n;
cin >> n;
cout << DP[n] << "\n";
}
}