이번 포스팅에서 내용과 예시는 'Bradley Efron' 교수님께서 쓰신 "Large-Scale Inference"와 "Computer Age Statistical Inference: Algorithms, Evidence and Data Science"를 참고했다. 1편을 안보셨으면 먼저 "다중검정문제와 해결법"을 보고 오시는 것을 추천합니다. 이전 1편에서 설명했듯이 다중검정문제는 단일검정문제와 비교했을 시 매우 까다로운 문제다. 해결법으로 제시된 본페로니 교정도 매우 보수적인 검정법으로 검정력을 잃게 된다는 단점이 존재한다. 역사적으로 많은 연구를 진행했고 비교적 최근 1995년에 Benjamini와 Hochberg가 "FDR" 개념을 소개하면서 많은 발전을 이루었다고 한다.

---

FDR(False Discovery Rate)

FDR의 정의

그림 출처: Large-Scale Inference, Bradley Efron

통계학에서 많이 등장하는 $2 \times 2$ 분할표를 통해 알아보자. 위의 분할표가 가설 검정의 결과를 분할표로 나타낸 것이다. 일반적으로 하나의 검정을 할 시에는 분할표를 만들 이유가 없지만 다중검정에서는 분할표를 작성할 수 있겠다. 분할표에서 가로는 실제 참값이다(모르지만). 세로는 결정 규칙($D$)에 의해 결정된 결과이다. 결정 규칙($D$)는 하나의 예로 유의수준보다 작은 p-value를 가지면 귀무가설을 기각하는 규칙을 들 수 있다. 분할표에서 결정 규칙에 의해 총 $R$개의 가설을 귀무가설이 아니라고 판단했다. 그 중 $a$개는 실제로 귀무가설이다. 따라서 잘못된 판단의 비율을 다음과 계산할 수 있다.

하지만 $\text{Fdp}$ 값은 우리가 알 수 없다. 왜냐하면 $a$를 모르기 때문이다. 어떤 가정하에서는 기댓값을 생각할 수 있다(이 부분은 아직 공부가 부족하다).

$\text{Fdp}$의 기댓값을 $\text{Fdr}$로 정의한다.

본페로니 교정은 $\text{FWER}$(하나의 가설이라도 잘못 기각할 비율)을 통제했지만 이는 너무 보수적인 방법이라 $\text{FDR}$을 통제하는 방법이 주류로 자리잡고 있다.

FDR control

앞서 말한 $\text{FDR}$을 통제하는 방법은 무엇일까? 방법은 간단하지만 그 원리는 단순하지가 않다. 이 포스팅에서는 방법만 소개하고 넘어가겠다.

어떤 결정규칙($D$)가 있을 때, $\text{FDR}$을 $q$ 수준으로 통제한다는 것은 다음과 같다.

그럼 결정규칙 $D$는 어떤 것일까?

p-value들의 순서통계량 $\{p_{(1)}, \dots, p_{(N)}\}$을 정의하고 다음 식을 만족하는 검정의 인덱스 중 가장 큰 인덱스를 $i_{max}$라고 하자.

$\text{FDR}$을 $q$ 수준으로 통제하는 규칙 $D$는 $p_{i} \leq p_{i_{max}}$를 만족하는 검정들은 기각하고 나머지는 채택한다. 이러한 방법을 제안한 사람들의 이름을 따서 Benjamini-Hochberg 알고리즘, 줄여서 BH 알고리즘이라고 한다. BH 알고리즘에서 정확하게 얘기하면 규칙 $D$는 $\pi_0 q$ 수준으로 $\text{FDR}$을 통제하지만 $\pi_0 \approx 1$이므로 크게 문제되지 않는다.

추가적으로 앞서 설명한 홈의 알고리즘과 BH 알고리즘의 임계치의 크기를 비교해보면

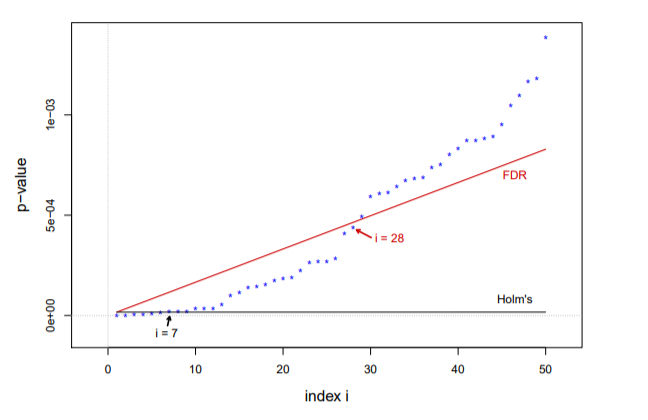
로 p-value가 작은 쪽에서 거의 선형적으로 증가한다($N$은 $i$에 비해 매우 크다). 즉, BH의 임계치가 더 크므로 더 많이 기각하는 것을 알 수 있다. 보수적인 FWER 방법의 문제를 해결했다고 볼 수 있다. 아래의 그림을 보면 BH 알고리즘은 28개를 기각하는 반면에 홈의 방법은 7개를 기각하며 빨간선과 검은선은 각각 BH 알고리즘과 홈의 방법의 임계치를 나타낸다. 그림에서 보면 $i$가 커질수록 빨간선과 검은선의 차이가 커지는 것을 확인할 수 있다.

그림 출처: Computer Age Statistical Inference, Bradley Efron and Trevor Hastie

베이즈 거짓 발견율(Bayes false discovery rate)

베이지안 관점에서 $\text{FDR}$을 생각해보자. 두 그룹이 존재한다. 각 그룹의 비율은 $\pi_0$, $\pi_1$이며 성격은 귀무가설의 분포$(f_0)$를 따르는 그룹과 그렇지 않은 분포$(f_1)$를 따르는 그룹이다. 앞선 포스팅과 연관지어서 생각해보면 6033개의 유전자는 귀무가설을 따르는 그룹과 대립가설을 따르는 그룹으로 나누어질 것이다. 그리고 두 그룹의 비율을 정확하게 알 수 없지만 $\pi_0 \approx 1$일 것이고 $\pi_1 \approx 0$일 것이다(대립가설의 유전자는 매우 적을 것이다). 두 그룹의 분포를 가지고 환자와 일반인의 유전자 특징의 차이값을 정규화한 $z$ 값의 혼합분포(mixture density), $f(z)$로 표현할 수 있다.

$f_0$는 표준정규분포의 밀도함수로 사용하고 대립가설의 밀도함수, $f_1$는 알 수 없다. $F_0, F_1$은 각각 $f_0, f_1$의 분포함수이다. $S_0(z) = 1 - F_0(z), S_1(z) = 1 - F_1(z)$로 정의하면 $S_0(z_0)$는 $z$가 $z_0$를 초과할 확률이 된다. 즉, $\int_{z_0}^{\infty}f_0(z)dz$이다.

만약, $i$번째 유전자의 $z_i$ 값이 기각역의 임계치 값 $z_0$를 넘었다고 가정하면 우리는 $i$번째 귀무가설을 기각할 것이다. 그런데 실제로는 $i$번째 유전자가 귀무가설을 따른다고 하자(실제로는 알 수 없지만). 그럼 조건부 확률은 베이즈 규칙을 활용하여 다음과 같이 계산할 수 있다.

그리고 이 확률은 우리가 결정 규칙에 의해서 잘못된 판단(귀무가설이 참인데 기각을 했으니)을 내릴 확률이다. 따라서, 이러한 확률을 "베이즈 거짓 발견율"라고 부른다.

$\text{Fdr}(z_0)$에서 귀무가설의 분포는 표준정규분포, $\pi_0$도 1에 가까운 값으로 가정하므로 알 수 없는 값은 $S(z_0)$이다. 현재 데이터를 통해 $S(z_0)$를 단순하지만 대수의 법칙에 의해 불편추정량(unbiased estimator)으로 다음과 같이 추정할 수 있다.

단순하게 전체 N개의 유전자 중, $z_0$보다 큰 $z_i$를 가지는 유전자의 비율이다. $\hat{S}(z_0)$를 $\text{Fdr}(z_0)$에 대입하여 플러그인 추정치를 만들 수 있다.

$i$번째 가설의 p-value, $p_i = S_0(z_i)$이고 또한 $\hat{S}(z_{(i)}) = i/N$이다($p_{(i)}$와 $z_{(i)}$는 순서가 반대이므로). 이제 위와 같은 혼합분포에서 BH 알고리즘를 다시 적어보면 다음과 같이 이어진다.

BH 알고리즘을 베이지안 관점에서 보면 $\hat{\text{Fdr}}$은 귀무가설의 경험적 사후분포(empirical Bayes posterior probability), 즉 $z_i$가 주어졌을 때, 귀무가설일 확률이 미리 정한 $\pi_0 q$보다 작으면 기각하는 방법으로 해석할 수 있다.

FDR의 최근 연구

p-value들의 correlation 구조를 고려한 연구

BH 알고리즘은 p-value들의 독립을 가정한다. 최근 연구들은 p-value들의 종속적인 구조를 고려한 $\text{FDR}$ 통제 방법을 개발하고 제안한다. 그 중에서 2019년 JRSSB에 실린 연구를 소개를 아래의 발표자료로 대신한다. 아래의 연구는 p-value들의 다양한 종속적인 구조(순서열, 공간 등)를 고려할 수 있는 일반적인 BH 알고리즘은 SABHA 알고리즘을 제안한다.

Multiple testing with the structure adaptive Benjamini-Hochberg algorithm(Li, A., & Barber, R. F., 2019)

참고자료

• Large-Scale Inference, Bradley Efron
• Computer Age Statistical Inference: Algorithms, Evidence and Data Science, Bradley Efron, Trevor Hastie