CNN(합성곱 신경망)
7.1 전체 구조
- Affine-ReLU(=완전 연결 신경망)
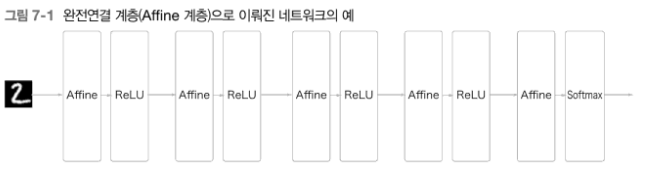
- Conc-ReLU-(Poolong)
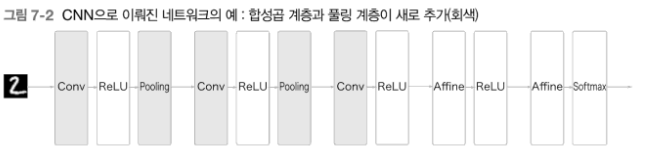
- 3차원 데이터 같이 입체적인 데이터가 흐른다는 점에서 차이
7.2 합성곱 계층
7.2.1 완전 연결 계층의 문제점
데이터의 형상을 무시
: 3차원-> 1차원 평탄화 하는 과정에서 공간적 정보(차원 별 정보)가 무시됨(모두 같은 차원으로 취급)
- 합성곱 계층은 형상을 유지(3차원 -> 3차원)
- feature map(특징맵) : CNN에서 합성곱 계층의 입출력 데이터
7.2.2 합성곱 연산
-
기본적인 예
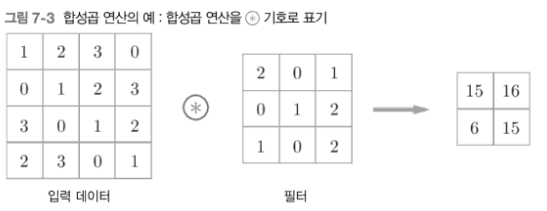 (커널=필터)
(커널=필터) -
편향 추가
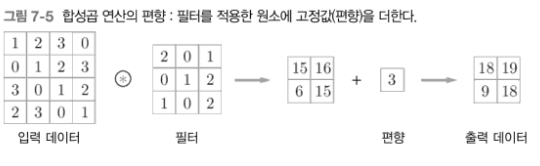
7.2.3 패딩
- 출력의 크기를 조절하기 위해 사용
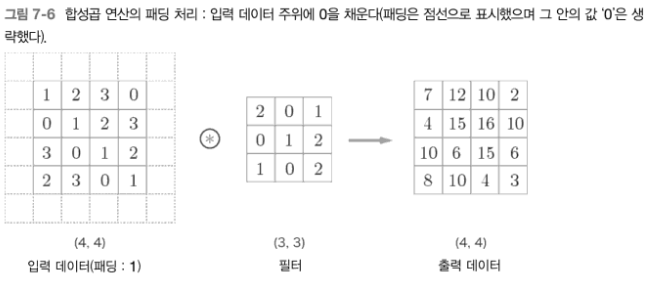
7.2.4 스트라이드
- 윈도우가 몇 칸씩 이동할지 결정
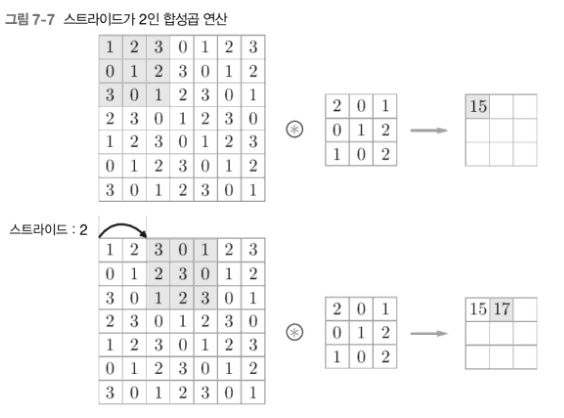
7.2.5 출력의 크기 계산
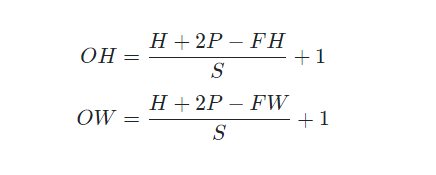
입력의 크기(H,W),패딩 P, 필터 크기(FH,FW), 스트라이드(S), 출력의 크기 (OH,OW)
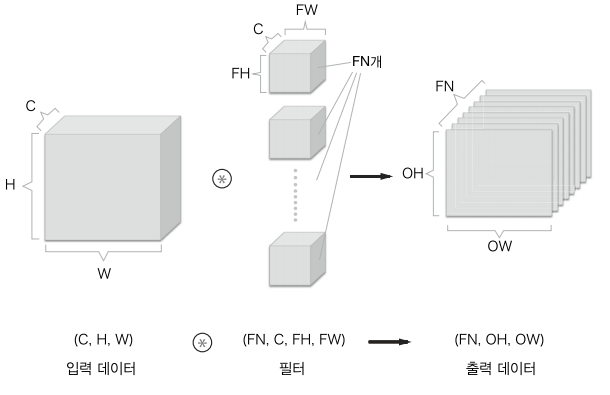
채널 수까지 생각
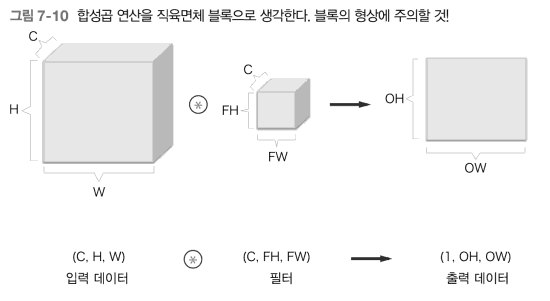
- 채널 마다 합성곱 연산을 수행, 그 결과들을 더해서 하나의 채널의 출력을 얻는다.
- 필터의 개수를 늘려 채널 수를 조절 할 수 있음
- 개수는 가장 앞에 씀(numpy에서)
배치 처리

- (HxW,C)형태 N개의 데이터 각각에 FN개의 필터가 곱해지며, (OHxOW,FN)이 N개가 됨
7.3 풀링
: 세로 가로 방향의 크기를 줄임
이미지의 크기를 축소하는 것이 목표
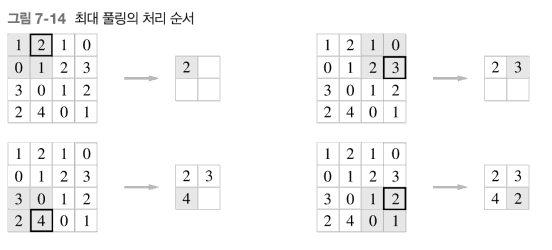
종류
- 최대 풀링, 평균 풀링
특징
- 매개변수가 없음
- 채널 수 변화가 없음
- 입력의 변화에 영향을 적게 받음
- 입력값 일부를 잃게 됨
7.4 합성곱/풀링 계층 구현
4차원 배열
(데이터 수, 채널, 높이, 너비)
7.4.1 im2col로 데이터 전개
3차원 데이터를 2차원으로 변환해 계산을 용이하게 하는 것
(정확히는 배치 안의 데이터 수까지 포함 한 4차원 데이터를 2차원으로 변환
데이터 수만큼 열이
늘어남)
- 3차원->2차원
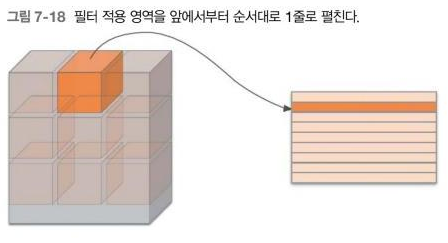
- 연산 과정
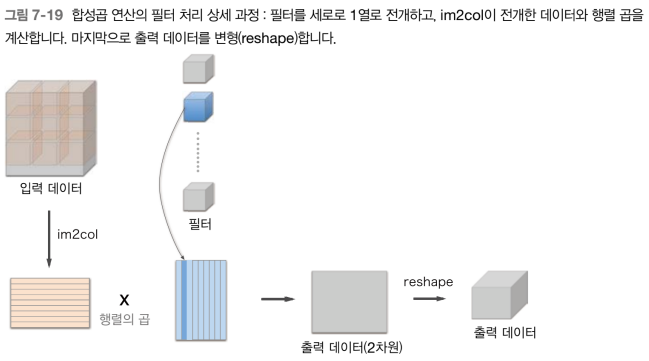
필터 각각을 세로로 1열로 전개, 필터의 개수는 열의 수(출력 시 차원의 수가 됨)
계산을 행렬의 곱으로 바꿈
출력 데이터는 다시 4차원으로 변형(reshape)
7.5 합성곱 계층 구현
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 중간 데이터(backward 시 사용)
self.x = None
self.col = None
self.col_W = None
# 가중치와 편향 매개변수의 기울기
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return outimcol을 이용해 행렬로 만들어 XW+b를 계산한 뒤 다시 이미지 데이터 형태로 만듦
7.6 CNN 구현
class SimpleConvNet:
"""단순한 합성곱 신경망
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 입력 크기(MNIST의 경우엔 784)
hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트(e.g. [100, 100, 100])
output_size : 출력 크기(MNIST의 경우엔 10)
activation : 활성화 함수 - 'relu' 혹은 'sigmoid'
weight_init_std : 가중치의 표준편차 지정(e.g. 0.01)
'relu'나 'he'로 지정하면 'He 초깃값'으로 설정
'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))초기화 인수로 주어진 합성곱 계층의 하이퍼파라미터를 딕셔너리에서 꺼냄
합성곱 계층의 출력 크기를 계산
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)# 계층 생성
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()순서가 있는 딕셔너리인 layers에 계층들을 차례로 추가
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""손실 함수를 구한다.
Parameters
----------
x : 입력 데이터
t : 정답 레이블
"""
y = self.predict(x)
return self.last_layer.forward(y, t)predic와 loss를 구함
def gradient(self, x, t):
"""기울기를 구한다(오차역전파법).
Parameters
----------
x : 입력 데이터
t : 정답 레이블
Returns
-------
각 층의 기울기를 담은 사전(dictionary) 변수
grads['W1']、grads['W2']、... 각 층의 가중치
grads['b1']、grads['b2']、... 각 층의 편향
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads역전파 구현
CNN 시각화하기
- 첫번째 층 가중치 시각화(필터의 가중치가 앞 데이터의 특성을 보여줌)

무작위-> 어느정도 규칙성(=이미지에 반응)
https://velog.velcdn.com/images%2Fkimkihoon0515%2Fpost%2F8ef1e2dd-6f6d-4169-a4d4-9e11d9b99ca6%2Fimage.png - 깊이에 따른 추출 정보의 변화
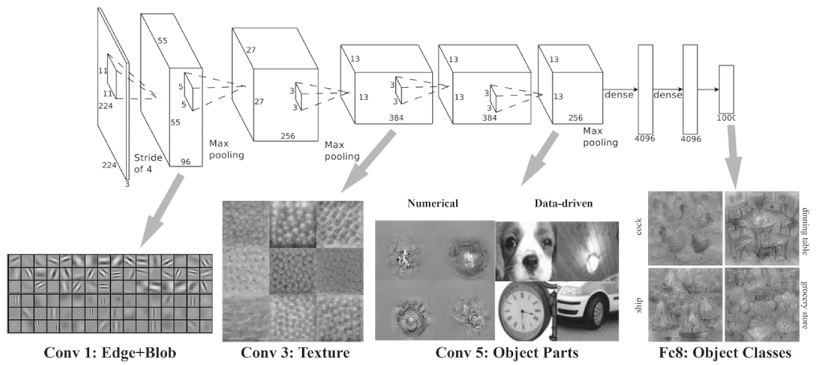
깊어질수록 복잡하고 추상화된 정보(국소적 정보->크게크게 봄, 고급 정보)
대표적인 CNN
LeNet
손글씨 숫자 인식 신경망
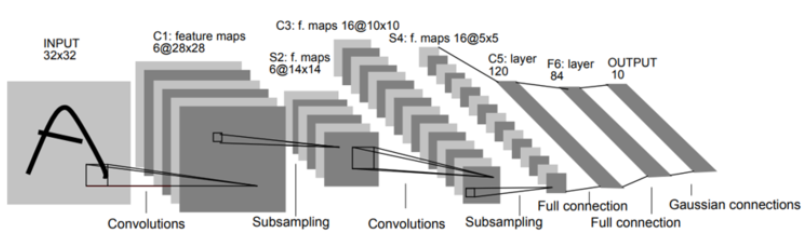
- 활성화함수로 Sigmoid함수를 사용함
- Subsampling(풀링)시 평균 풀링을 사용함
AlexNet
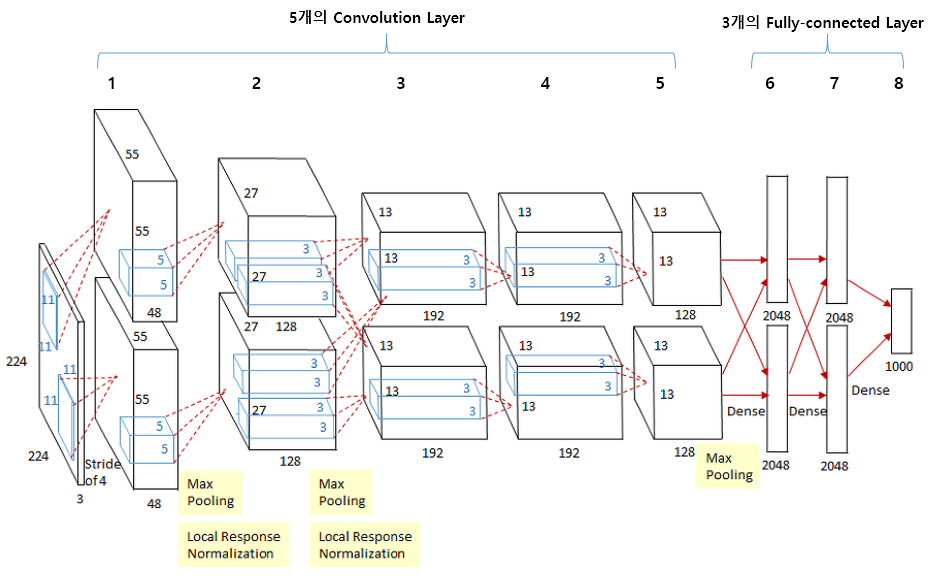
- 활성화 함수로 ReLU함수를 사용함
- Local Response Normalization(국소적 정규화)를 실시하는 계층을 이용함
- 드롭아웃을 사용함
- 최대 풀링 사용함
- 두개의 컨볼루션 레이어를 병렬로 사용해(입력 데이터 똑같이 모두 들어감) 각자 계산하고 나중에 합침
