오차역전파법
가중치의 매개변수의 기울기를 효율적으로 계산하기 위한 방법
1. 계산 그래프
책에선 계산그래프를 통해 설명하고 있음 (수식을 통한 방법이 아닌,)
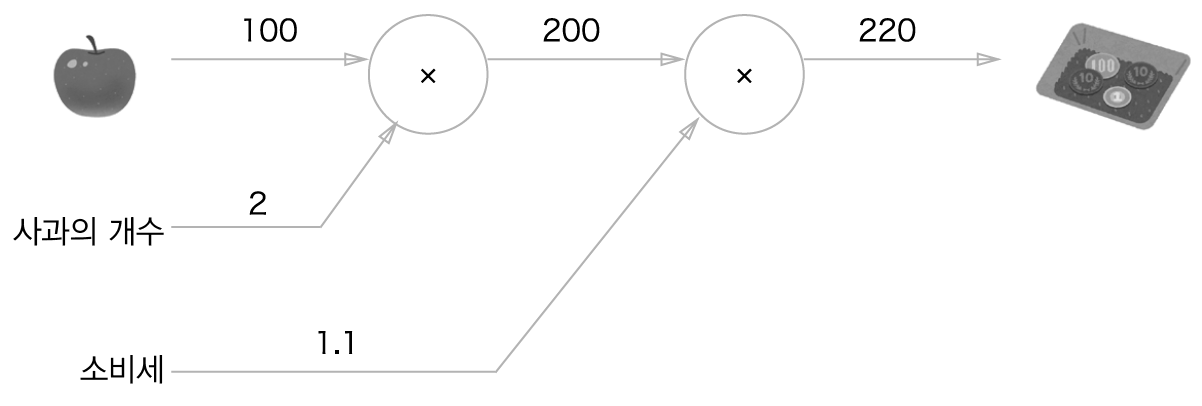
문제 1현빈 군은 슈퍼에서 1개에 100원인 사과를 2개 샀다.
이때 지불 금액을 구하자.
단, 소비세가 10% 부과된다.
-
계산 그래프를 사용하는 이유: 역전파를 통해 효율적으로 미분을 계산할 수 있다.
-
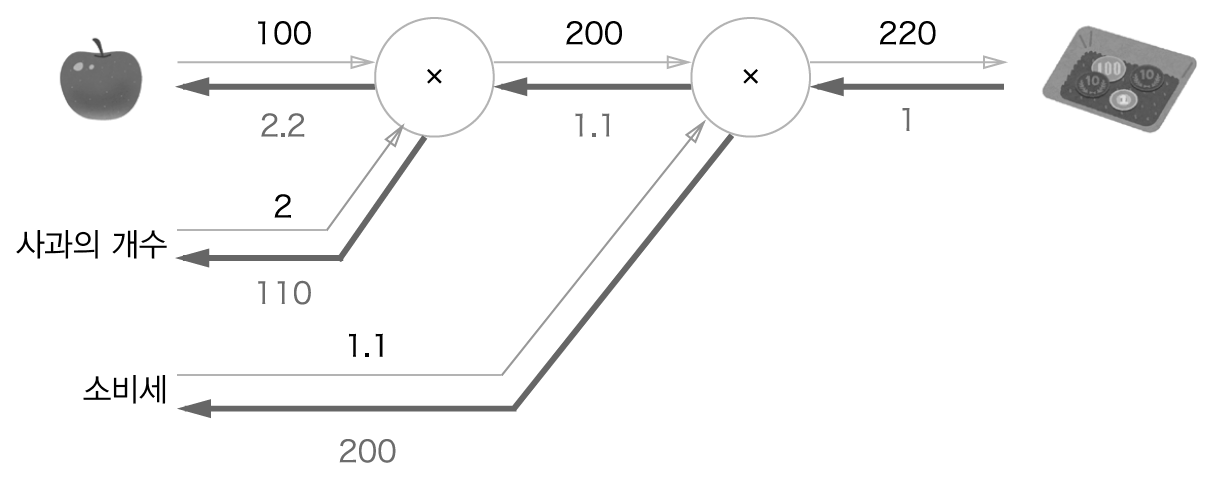
미분 값의 의미:
eg) 사과가격에 대한 지불 금액의 미분 = 사과값이 조금 올랐을 때 지불 금액이 얼마나 증가하냐
아래 그림에선) 사과가격이 1 오를 때 지불 금액이 2.2만큼 증가
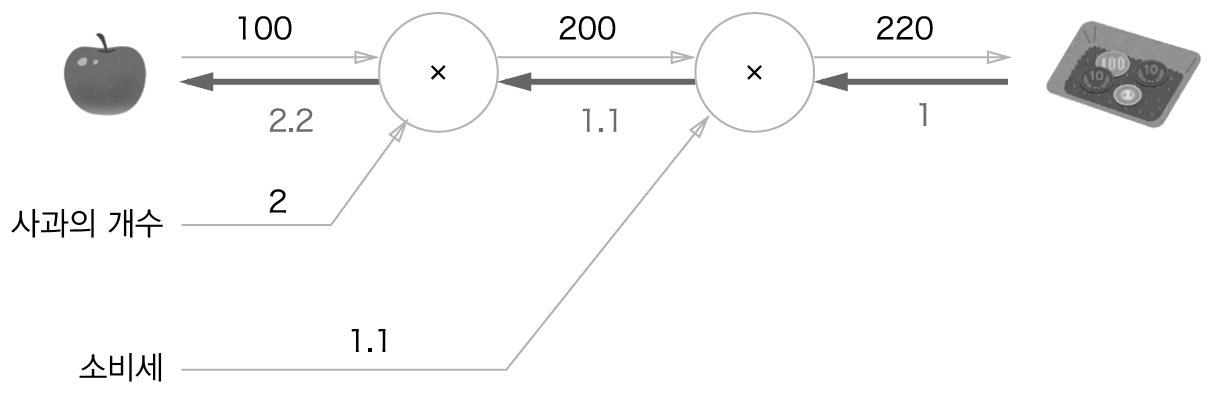
사과의 개수, 소비세에 대한 미분 값도 같은 과정을 통해 구할 수 있음
2. 연쇄법칙
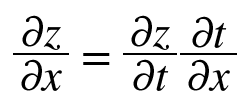

결국 역전파가 하는 것은 연쇄 법칙과 같다.
3. 역전파
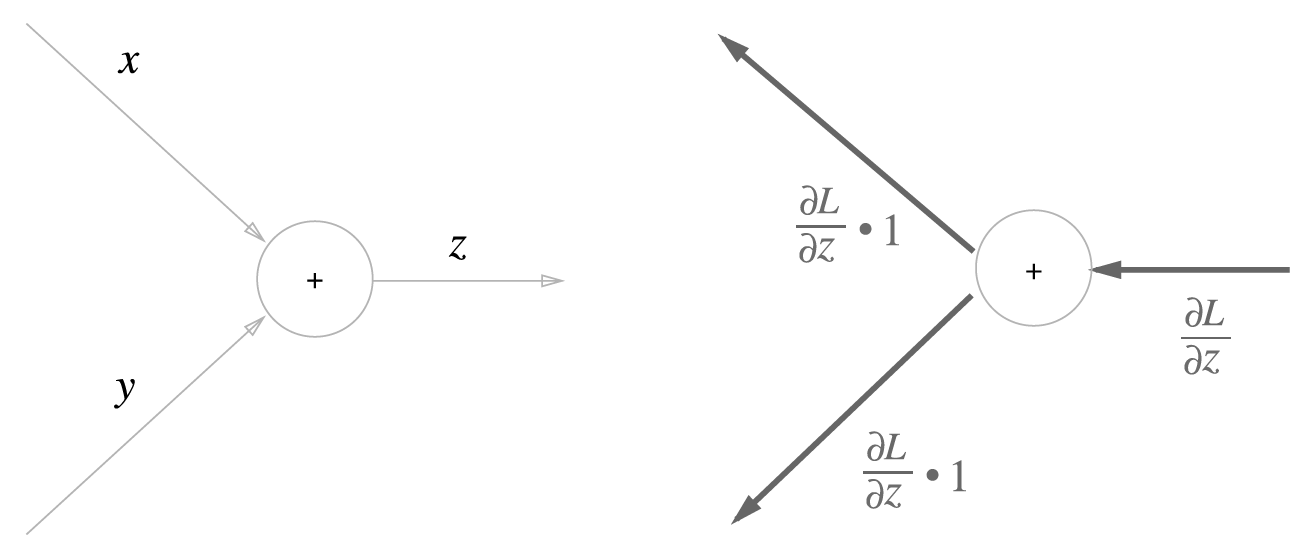
- 덧셈의 역전파
z = x+y
z = x+y의 미분 값 = 1
상류로부터의 값이 그대로 전해짐
- 곱셉의 역전파
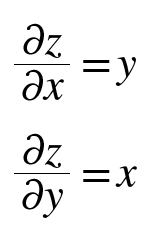
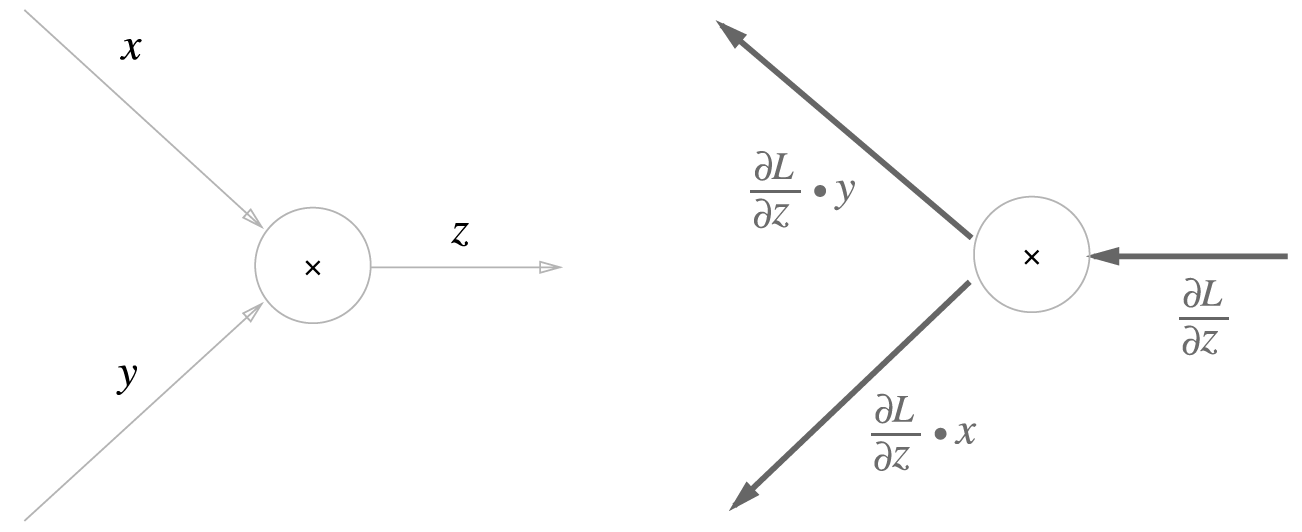
상류의 값에 입력신호들을 서로 바꾼 값을 곱해서 보냄
사과 쇼핑의 예)
4. 단순한 계층 구현
- 곱셈 노드를 MulLayer, 덧셈 노드를 AddLayer 이름으로 구현
- forward():순전파 와 backward():역전파
곱셉 노드
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # x와 y를 바꾼다.
dy = dout * self.x
return dx, dy사과 문제 구현
- MulLayer()로 순전파를 구현
from layer_naive import * apple = 100 apple_num = 2 tax = 1.1 mul_apple_layer = MulLayer() mul_tax_layer = MulLayer() # forward apple_price = mul_apple_layer.forward(apple, apple_num) price = mul_tax_layer.forward(apple_price, tax) print(price) #220
- backward()로 역전파 구현
# backward dprice = 1 dapple_price, dtax = mul_tax_layer.backward(dprice) dapple, dapple_num = mul_apple_layer.backward(dapple_price) print(dapple, dapple_num, dtax) # 2.2, 110, 200
5. 활성화 함수 계층 구현
1. Relu
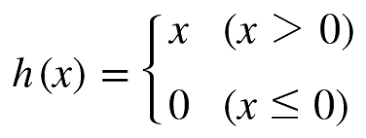
순전파가
0 이상일 땐 (1을 곱해서) 그대로 보내고
0 이하 일땐 (0을 곱해서) 차단함
2. sigmoid
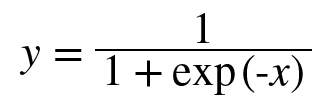
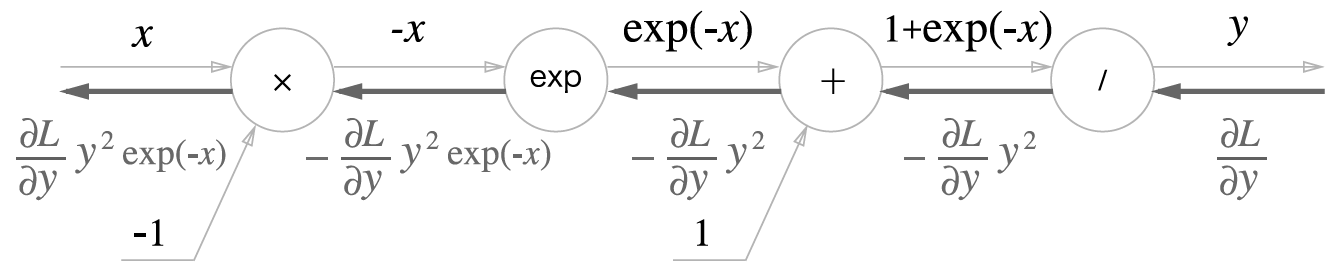
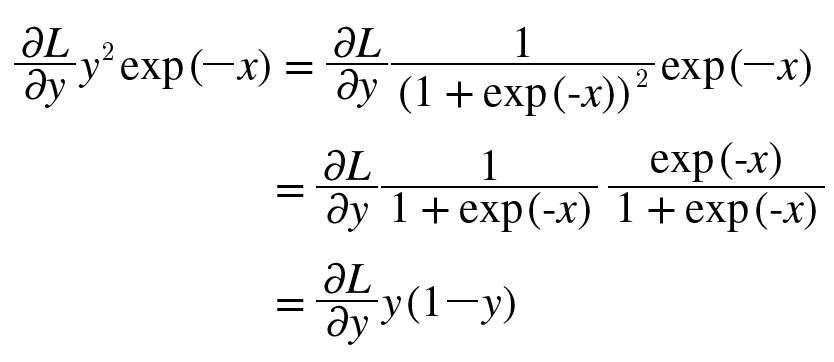
결국
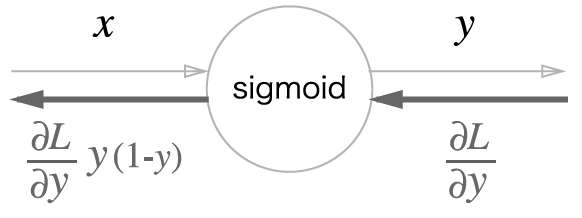
3. affine 계층 구현
-> 행렬을 고려함
1) 데이터 하나의 affine 계층
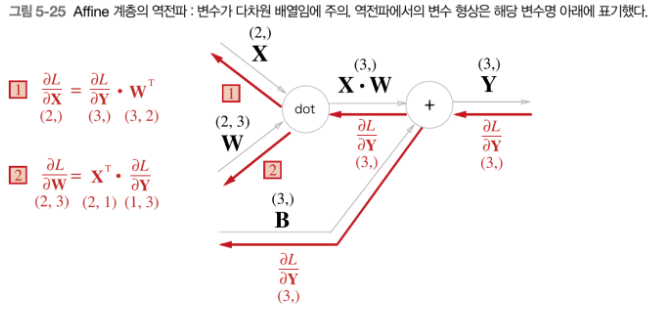
- numpy 에서 (2,)는 (1,2)의 형태로 계산
- 위의 순전파 계산은 (1,2) x (2,3) +(1,3) 의 형태
- 1,2에선 서로의 입력값을 바꿔서 곱해줌
2) 배치용 affine 계층
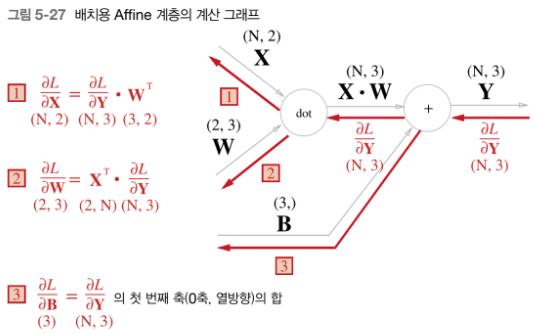
-
3에서 bias의 역전파는 각 샘플에 대한 미분의 총합으로 구함
-
N(배치사이즈)=2인 경우 예시
>>>dY = np.array([[1,2,3,], [4,5,6]) #각 샘플에 대한 (dL/dy)미분 값들
>>> dy
array([[1,2,3],
[4,5,6]])
>>> dB = np.sum(dY,axis =0) #각 샘플에 대한 미분 값들의 합
>>>dB
array([5,7,9])3. Softmax-with-Loss 계층
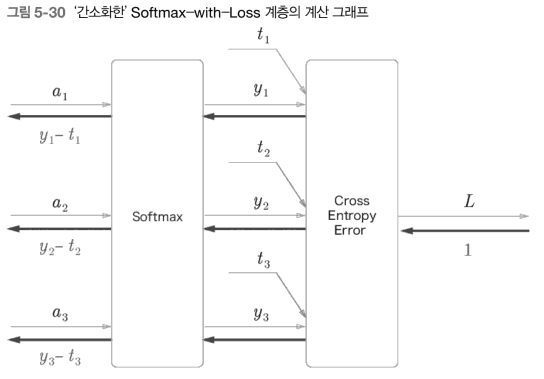
- y는 Softmax 계층의 출력
- t는 정답 레이블
- y-t는 Softmax 계층의 출력과 정답 레이블의 차분
Softmax 계층의 역전파는 y-t라는 결과를 내놓음.
신경망에서 오차가 앞 계층에 전해지는 것.
즉, 거꾸로 올라가 보면,
-> y-t라는 결과가 Softmax 계층에서 앞 계층들로 전해짐.
-> 앞 계층들에 있는 가중치들은 이를 통해 미분값이 결정됨.
-> 가중치의 기울기를 통해 손실함수를 적게 하는 방향으로 가중치 갱신
-> 반복
6. 오차역전파법을 사용한 신경망 구현
클래스의 메서드
# x : 입력 데이터, t : 정답 레이블
# 수치 미분 방식 def numerical_gradient()
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 오차역전파법 방식 def gradient()
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads신경망 구현
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch) # 수치 미분 방식
grad = network.gradient(x_batch, t_batch) # 오차역전파법 방식(훨씬 빠르다)
#이 부분만 바뀜!
# 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)