자 열 네번째 키워드인 '벡터의 내적과 외적'을 알아보겠다.

일단 이번 키워드는 아마 꾸준히 공부할 것으로 예상되니 간략하게 알아보고
나중에 더 탐구해서 글을 작성 하겠다.

내적이 뭐에요?

내적은 두 벡터 간의 연산으로, 스칼라 값을 반환합니다. 보통 두 벡터 사이의 각도와 크기를 비교하는 데 사용된다. 벡터 A와 벡터 B의 내적은 다음과 같이 정의된다.
𝐴⋅𝐵 = ∣𝐴∣∣𝐵∣ cos(𝜃) 여기서 ∣𝐴∣와∣𝐵∣는 각각 벡터 A와 B의 크기(또는 길이)이고,
θ는 두 벡터 사이의 각이다. 내적이 0이 되는 경우 두 벡터는 수직이라고 말할 수 있다.

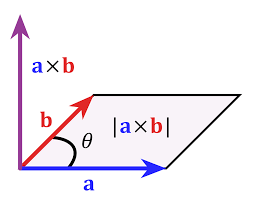
외적이 뭐에요?

외적은 두 벡터의 수직인 성분을 이용하여 새로운 벡터를 생성한다. 이 새로운 벡터는 원래 두 벡터가 이루는 평면에 수직이다. 외적은 다음과 같이 정의된다.
𝐴×𝐵=∣𝐴∣∣𝐵∣sin(𝜃)𝑛 여기서 ∣𝐴∣와 ∣𝐵∣는 각각 벡터 𝐴와 𝐵의 크기이고, 𝜃는 두 벡터 사이의 각이다. 𝑛은 두 벡터가 이루는 평면에 수직이고 크기는 ∣𝐴∣∣𝐵∣sin(𝜃)인 새로운 벡터이다.

내적과 외적을 정리

[내가 생각을 정리한 결과이다.]

내적 : 앞뒤를 판단할 수 있음

• A와 B를 내적한 값이 0이상일때 B가 A보다 앞에 있음
• A와 B를 내적한 값이 0이하일때 B가 A보다 뒤에 있음
• A와 B를 내적한 값이 0일때 A와 B는 수직을 이루고 있음

외적 : 왼쪽과 오른쪽을 판단할 수 있음

• 벡터 y와 벡터 z 를 외적 하면 벡터 x
• 벡터 z와 벡터 x 를 외적 하면 벡터 y
• 벡터 x와 벡터 y 를 외적 하면 벡터 z
• 0보다 크면 오른쪽, 작으면 왼쪽, 같으면 같은 위치

결론 - 느낀 점

후... 진짜 벡터에 대해 알고 있었지만 이렇게 깊게 공부한적은 처음이다.

나의 한계를 넘은거 같기도 하면서 한계가 느껴지는 키워드이기도 했다.

이 분야는 더 공부하여 마스터해야겠다.