자, 96번째 키워드인 이진 검색 트리(BST)를 알아볼 것이다.

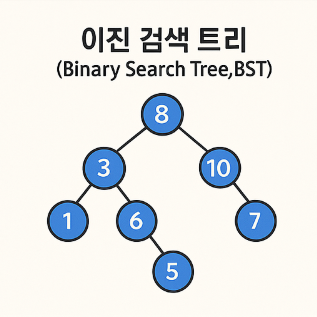
이진 검색 트리는 Binary Tree의 한 종류로, 각 노드가 최대 두 개의 자식노드를 가지는 것을 의미한다.

만족하는 조건은 왼쪽 서브트리가 항상 루트보다 작고, 오른쪽 서브트리는 항상 루트보다 크다는
조건을 만족하게 된다.

이러한 구조는 트리의 탐색, 삽입, 삭제 등의 연산을 효율적으로 수행이 가능하다.

설명

BST의 정렬된 상태를 Tree 구조로 유지를 한다는 점이 핵심이다. 재귀적인 성질이 강하며
중복을 허용하지 않는 경우가 많다.
왜냐하면 정렬된 구조에서 중복이 된다면 탐색회수가 늘어나기 때문이다.

• 삽입 연산시에는 현재 노드와 값을 비교해 왼쪽 또는 오른쪽으로 이동한다.
• 탐색 시도 시에도 같은 방식으로 깊이를 따라 이동한다.
• 삭제는 자식 노드의 개수(0개, 1개, 2개)에 따라 처리 방식이 달라지게 된다.

Tree의 높이에 따라 성능은 천차 만별이 된다. 최악의 경우는 선형 탐색 수준으로 떨어질 우려가 있다.
이 단점을 해결하기 위해 나온 방안은 AVL Tree, Red-BlackTree 등의 균형이진검색트리가 나오게 되었다.

장점

1. 평균적으로 탐색, 삽입, 삭제 O(log n)의 성능
2. 정렬된 데이터의 계층적 구조 표현에 적합
3. 중위 순회를 통해 정렬된 순서 출력 가능
4. 재귀적 구조로 분할 정복 등 다양한 알고리즘과 결합 용이

단점

1. 데이터가 정렬된 상태로 삽입이 되면 트리 불균형 발생 -> O(n)으로 성능 저하
2. 균형 유지 알고리즘이 없다면 실 사용에 제약이 많음
3. 메모리 사용량이 배열 기반 구조보다 많음

사용 예시

• 탐색 기반 알고리즘 구현 (예 : 캐릭터 Status 의 우선순위 처리)
• 자동 완성 시스템에서 문자열 트리와 결합
• 컴파일러나 해석기에서 식 평가를 위한 트리구조