파괴되지 않은 건물
- skill의 최대 개수는 250,000이고, 배열은 최대 1000 X 1000 배열이다.
- skill은 무조건 루프를 돌아야 하기 때문에 으로 풀게 되면 안된다.
- 그래서 생각난 것이 부분 배열 합이다.
부분 배열 합
2차원배열에서 부분 배열의 합을 구하는 방법을 알아보자. 이중 for를 이용해서 구할 수 있지만 시간복잡도가 O(n^2)이 되기 때문에 더 효율적인 방법을 찾아보자.
누적합
다음과 같은 배열이 있다고 가정하자.
- arr = [3, 5, 7, 1, 4]
- sum_list = [3, 8, 15, 16, 20]
위 배열에서 연속된 구간의 합, 예를들어 arr[1]부터 arr[3]까지의 합을 구하려고 한다면 3개의 원소값을 참조해야한다.
이러한 점을 보완하기 위해서 누적합 수열 sum_list를 도입한다.
sum_list[i]는 arr[0]부터 arr[i]까지의 모든 원소의 합을 값으로 갖는다. 또한 arr[i]부터 arr[j]까지의 부분합은 sum_list[j] - sum_list[i-1]로 정의할 수 있다.
누적합 배열의 성질
- sum_list[0] = arr[0]
- sum_list[i] = sum_list[i - 1] + arr[i]
- sum_list[n] = arr[0] + arr[1] + ... + arr[n-1] + arr[n]
- arr[i] + arr[i + 1] + ... + arr[j-1] + arr[j] = sum_list[j] - sum_list[i-1]
누적합을 활용한 빠른 부분합 계산
1차원 배열일 경우 반복문을 통한 구간합이 O(n)이고, 2차원 배열은 O(n^2)이다. 하지만 누적합 배열의 4번째 특징을 사용해서 연속된 임의의 구간의 합을 O(1)의 시간복잡도로 구할 수 있다.
2차원 누적합
위의 개념을 2차원으로 확장해보자. 이차원 배열에 대한 누적합 배열 또한 2차원 배열이 된다. 직사각형 형태의 배열에 포함되는 직사각형 구간의 원소의 합을 빠르게 구할 수 있다.
이차원 배열 a(i, j)와 누적합 배열 S(i, j)가 있다고 가정하자.
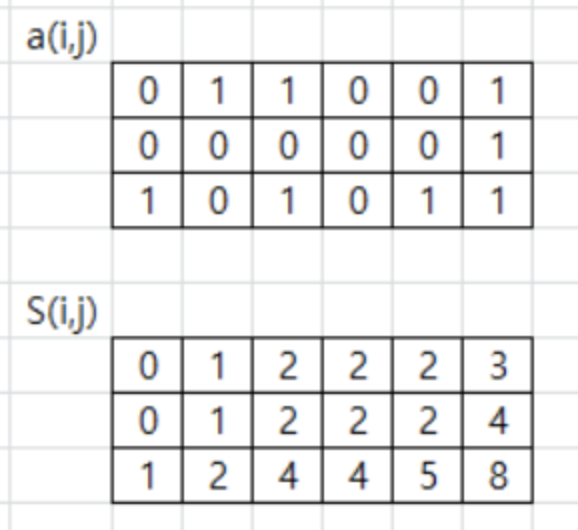
좌측 상단을 a(1, 1)이라 할 때, S(i, j)는 a(1, 1)과 a(i, j)를 양 대각 끝 꼭짓점으로 하는 직사각형 범위 면적 안의 모든 a원소의 합으로 정의된다.
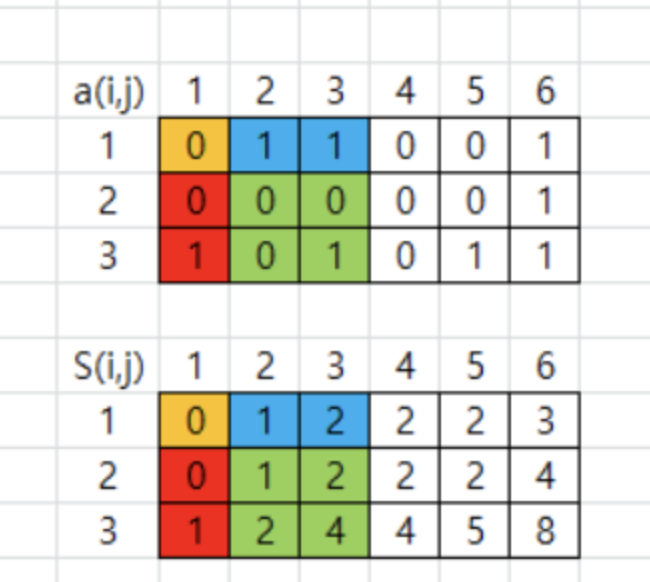
따라서 a(2, 2) ~ a(3, 3)의 부분합을 구해보자.
S(3, 3) 값에서 S(1, 3) 값을 빼고, S(3, 1)값을 뺀다. 이때 S(1, 1)은 S(1, 3)과 S(3, 1)에 의해서 2번 빼진 셈이니 S(1, 1)을 더해주면 초록색 부분의 구간합이 된다.
이를 정리하면 다음과 같다.
-
2차원 배열 arr이 있을 때, arr[x1][y1]부터 arr[x2][y2]까지의 부분 배열의 합을 Range(x1, y1, x2, y2)라 하자.
-
그리고 누적합 배열 S로 다음과 같이 정의된다.
-
Range(x1, y1, x2, y2) = S(x2, y2) - S(x1, y2) - S(x2, y1) + S(x1, y1)
이차원 누적합 배열 구하기
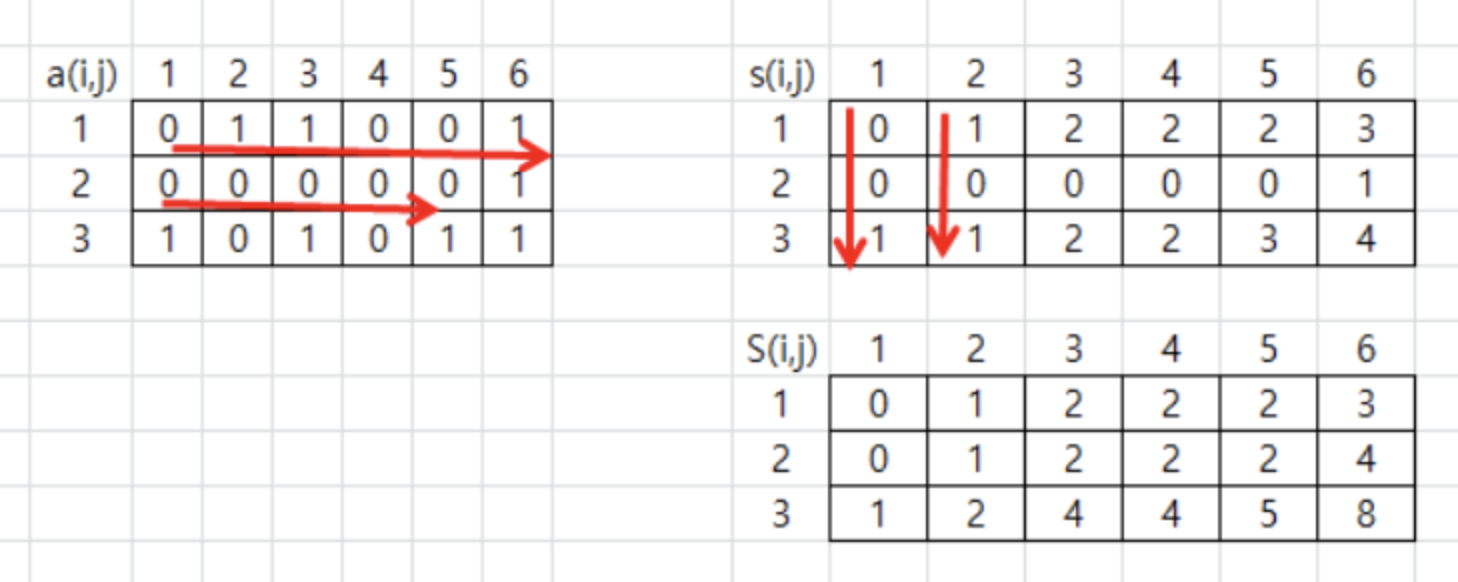
-
2차원 배열의 누적합 배열을 구하는 방법은 위와 같다.
-
a(i, j)에서 행방향으로 누적합을 구한다.
-
행 누적합에 대해서 열방향으로 누적합을 구한다.
결론 코드
def solution(board, skill):
answer = 0
temp = [[0 for _ in range(len(board[0]) + 1)] for _ in range(len(board) + 1)]
for type, r1, c1, r2, c2, degree in skill:
temp[r1][c1] += degree if type == 2 else -degree
temp[r1][c2 + 1] += -degree if type == 2 else degree
temp[r2 + 1][c1] += -degree if type == 2 else degree
temp[r2 + 1][c2 + 1] += degree if type == 2 else -degree
# 부분합을 구하기 위해 temp 배열 초기 설정
# 시작 인덱스에는 더해줘야할 수
# 마지막 인덱스 + 1에는 시작 인덱스와 반대 부호
# 그렇게 한 후 나중에 부분합을 하게 되면 그 범위에 있는 사각형에는 다 같은 데미지를 줄 수있다.
for i in range(len(board)):
for j in range(len(board[0])):
temp[i][j + 1] += temp[i][j]
# 열을 따라 부분합 먼저 계산
for j in range(len(board[0])):
for i in range(len(board)):
temp[i + 1][j] += temp[i][j]
# 행을 따라 부분한 계산
for i in range(len(board)):
for j in range(len(board[0])):
board[i][j] += temp[i][j]
if board[i][j] > 0:
answer += 1
return answer