병합 정렬 (Merge Sort)

1. 병합 정렬이란?

합병 정렬은 분할 정복 기법으로 만들어진 정렬 방법입니다. 주어진 배열을 원소가 하나만 남을 때까지 쪼갠 후, 다시 크기를 비교하며 원래 크기의 배열로 합치는 방법입니다.

분할 정복과 DP(Dynamic Progrmaing) 기법의 차이는?
두 방법 모두 문제를 잘게 쪼개서 작은 단위로 분할해 문제를 해결한다는 점은 동일하지만, 분할 정복 기법은 부분 문제에 중복이 없기 때문에 메모이제이션(이전에 계산한 값을 저장) 기법을 사용하지 않고, 동적 계획법은 사용한다는 차이가 있다.

아래 코드는 DP의 가장 대표적인 예시인 피보나치입니다. memo라는 객체에 부분 문제의 해(중간 결과)를 저장하는 것을 볼 수 있습니다.

const memo = {};

function fibonacci(n) {
  if (n <= 1) {
    return n;
  }

  if (memo[n]) {
    return memo[n];
  }

  memo[n] = fibonacci(n - 1) + fibonacci(n - 2);
  return memo[n];
}

console.log(fibonacci(10));  // 출력: 55

2. 합병 정렬의 원리

기본적인 원리는 다음과 같습니다.
1. 배열을 원소가 하나가 남을 때까지 계속 둘로 쪼갭니다.

[6, 5, 3, 1, 8, 7, 2, 4]
[6, 5, 3, 1] [8, 7, 2, 4]
[6, 5] [3, 1] [8, 7] [2, 4]
[6] [5] [3] [1] [8] [7] [2] [4]

2. 배열의 원소가 하나가 되었다면, 다시 두 개씩 합칩니다. (합치며 작은 숫자가 앞에 가도록 합니다.)

[5, 6] [1, 3] [7, 8] [2, 4]

3. 해당 방법을 반복합니다. 만약 배열의 값이 여러게라면, 각 배열 내에서 가장 작은 값 2개를 비교해 더 작은 값을 먼저 넣어줍니다.

[1, 3, 5, 6] [2, 4, 7, 8]

4. 마지막 배열도 각 배열에서 가장 작은 2개의 값을 비교해 더 작은 값을 먼저 넣어주면 정렬이 됩니다.

[1, 2, 3, 4, 5, 6, 7, 8]

3. JS 코드

JS 코드로 구현한다면 다음과 같습니다. 아래 코드에서 merge 함수는 2,3,4 번을 담당하고, mergeSort 함수는 1번을 담당하고 있습니다.

// `merge` 함수는 두 개의 정렬된 배열 `left`와 `right`를 입력받아 하나의 정렬된 배열을 반환합니다.
function merge(left, right) {
  let result = [];  // 병합된 결과를 저장할 배열
  
   // left와 right 배열의 값이 모두 reuslt에 들어갈 때까지 while 문 실행
   while (left.length || right.length) {
     
     // 두 배열 모두 원소가 있을 때: 작은 값을 결과 배열에 추가
     if (left.length && right.length) {
       result.push(left[0] < right[0] ? left.shift() : right.shift());
       
       // `left` 배열만 원소가 있을 때: `left`의 원소를 결과 배열에 추가
     } else if (left.length) {
       result.push(left.shift());
       
       // `right` 배열만 원소가 있을 때: `right`의 원소를 결과 배열에 추가
     } else {
      result.push(right.shift());
     }
   }
  return result;
}

function mergeSort(arr) {
  // 배열의 길이가 1 이면 이미 정렬된 것으로 간주하고 그대로 반환합니다.
  if (arr.length === 1) {
    return arr;
  }

  // 배열을 두 부분으로 나눕니다.
  const mid = Math.floor(arr.length / 2);
  
  // 재귀적으로 `mergeSort` 함수를 호출하여 배열을 계속해서 둘로 쪼갭니다.
  // 그 후, `merge` 함수를 사용해 두 정렬된 배열을 병합합니다.
  return merge(mergeSort(arr.slice(0, mid)), mergeSort(arr.slice(mid)));
}

// 테스트 코드
const arr = [6, 5, 3, 1, 8, 7, 2, 4];
console.log(mergeSort(arr)); // 출력: [1, 2, 3, 4, 5, 6, 7, 8]

코드의 실행 순서

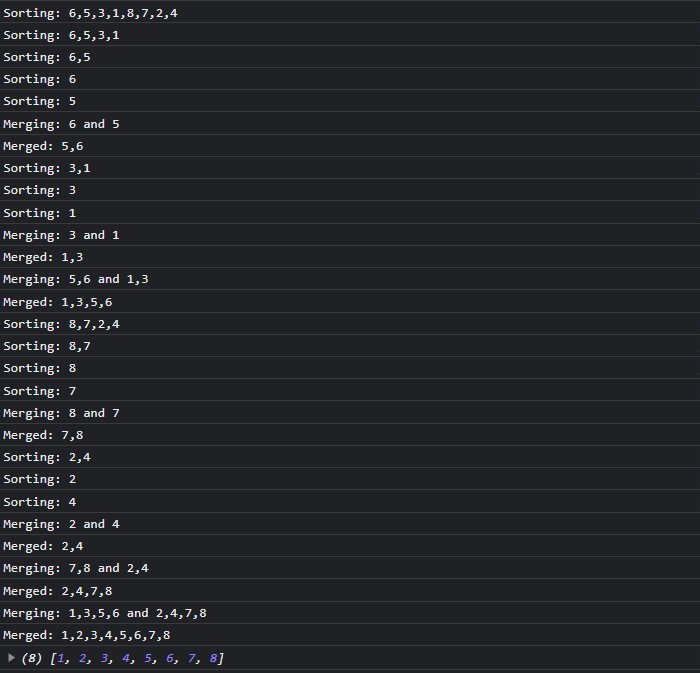
초기 호출: mergeSort([6, 5, 3, 1, 8, 7, 2, 4])
이 배열을 두 부분으로 나눕니다: [6, 5, 3, 1] 와 [8, 7, 2, 4]

재귀 호출: mergeSort([6, 5, 3, 1])
이 배열을 또 두 부분으로 나눕니다: [6, 5] 와 [3, 1]

재귀 호출: mergeSort([6, 5])
이 배열을 두 부분으로 나눕니다: [6] 와 [5]
이 두 배열은 길이가 1이므로 그대로 반환합니다.

병합: merge([6], [5]) → [5, 6]

재귀 호출: mergeSort([3, 1])
이 배열을 두 부분으로 나눕니다: [3] 와 [1]
이 두 배열은 길이가 1이므로 그대로 반환합니다.

병합: merge([3], [1]) → [1, 3]

병합: merge([5, 6], [1, 3]) → [1, 3, 5, 6]

재귀 호출: mergeSort([8, 7, 2, 4])
이 배열을 두 부분으로 나눕니다: [8, 7] 와 [2, 4]

재귀 호출: mergeSort([8, 7])
이 배열을 두 부분으로 나눕니다: [8] 와 [7]
이 두 배열은 길이가 1이므로 그대로 반환합니다.

병합: merge([8], [7]) → [7, 8]

재귀 호출: mergeSort([2, 4])
이 배열을 두 부분으로 나눕니다: [2] 와 [4]
이 두 배열은 길이가 1이므로 그대로 반환합니다.

병합: merge([2], [4]) → [2, 4]

병합: merge([7, 8], [2, 4]) → [2, 4, 7, 8]

최종 병합: merge([1, 3, 5, 6], [2, 4, 7, 8]) → [1, 2, 3, 4, 5, 6, 7, 8]
이렇게 최종적으로 정렬된 배열 [1, 2, 3, 4, 5, 6, 7, 8]이 반환됩니다