[3D] KD Tree와 BVH

출처: https://www.fwilliams.info/point-cloud-utils/sections/closest_point_on_mesh/

서론

3D 객체를 다룰 때 특정 Point에서 가장 가까운 객체를 찾아야하는 식의 Task를 많이 볼 수 있다.
예를 들어 화면상의 마우스가 어떤 객체를 가리키고 있는지 찾을 때 사용하는 Raycast도 비슷한 예시라고 볼 수 있다. (Ray와 교차하는 가장 가까운 객체를 찾아야 하므로)

가장 단순한 방법은 완전 탐색 방법이 있다.
minDistance를 Infinity로 설정해두고, 모든 삼각형(Polygon)을 순회하면서 해당 Polygon까지의 거리를 구해 minDistanced를 갱신하는 방식이다.
구현이 간편하지만 문제는 Polygon의 수가 늘어날수록 계산에 걸리는 시간이 선형적으로 증가하게 된다.

이를 해결하기 위해 마치 이진 탐색을 위해 배열을 정렬하는 것 같이, 3D 상의 polygon 또는 vertex들을 정렬하여 빠르게 탐색하도록 저장할 수 있는 자료구조가 바로 KD-Tree와 BVH이다.

KD Tree

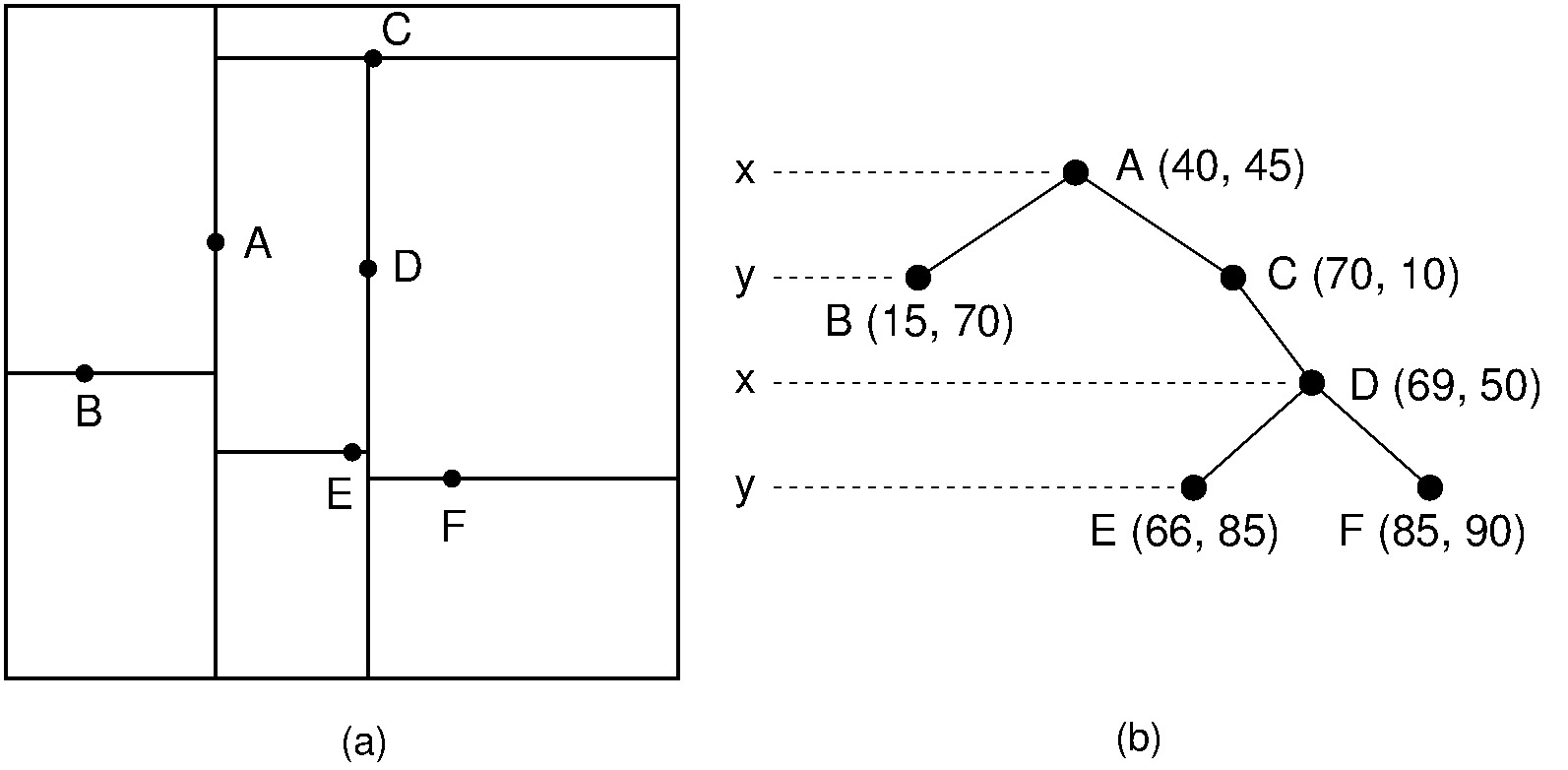
출처: https://opendsa-server.cs.vt.edu/ODSA/Books/CS3/html/KDtree.html

KD Tree는 K-Demension Tree의 약자로 K차원의 공간의 점을 구조화하는 이진 트리 자료구조이다.
즉 3D가 아닌 공간들에도 적용할 수 있다. (위 그림의 예시는 2D)

KD Tree 생성

과정은 다음과 같다.

0. 각 점들을 배열에 담는다.

[(40, 45), (15, 70), (70, 10), (69, 50), (66, 85), (85, 90)]

1. 첫번째 축(x축)에 대해 정렬하고 중앙값을 기준으로 배열을 쪼갠다

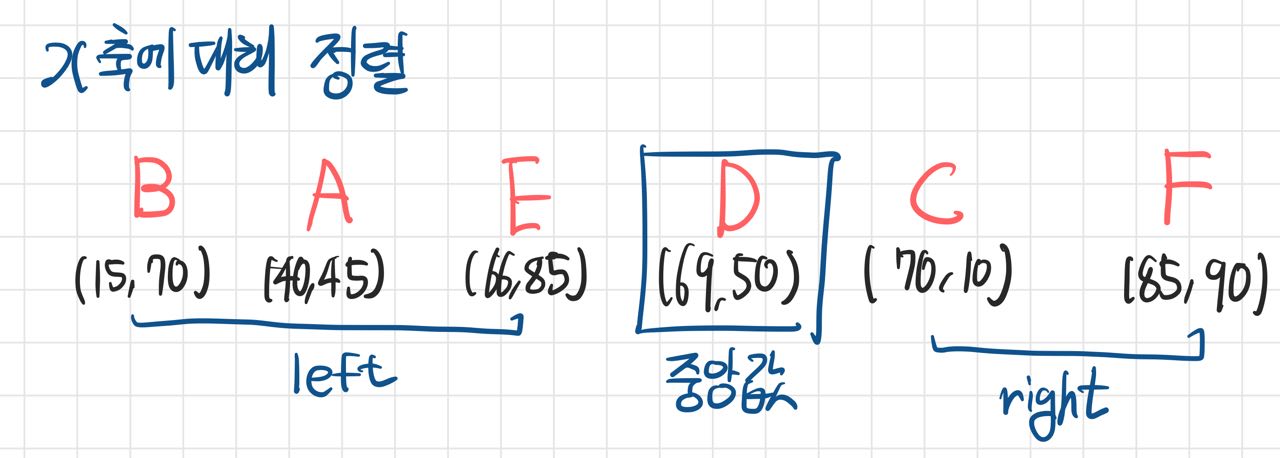
2. 쪼개진 배열별로 두번째 축(y축)에 대해 정렬하고 동일하게 쪼갠다

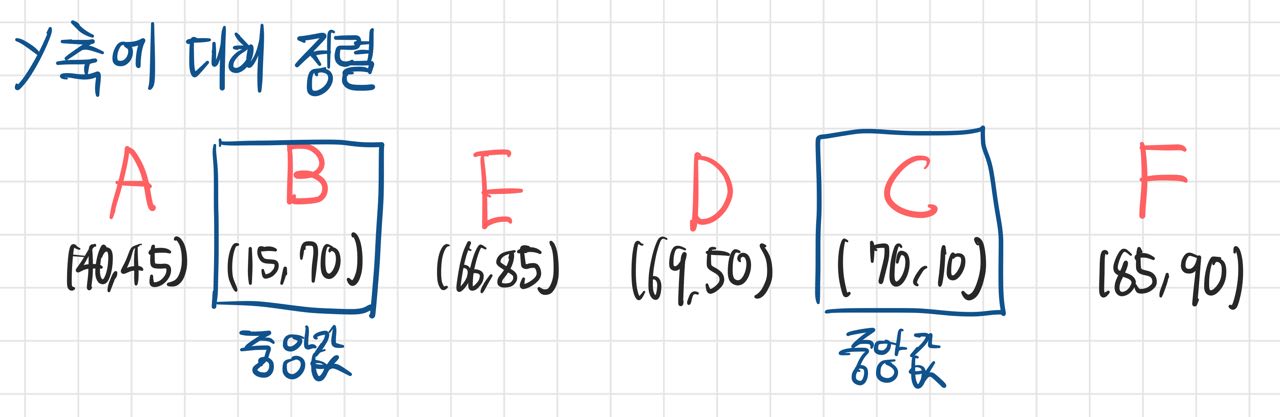
3. 다시 x->y->x->... 순으로 위 과정을 반복한다.

이렇게하면 아래 그림과 같은 트리구조가 완성된다.

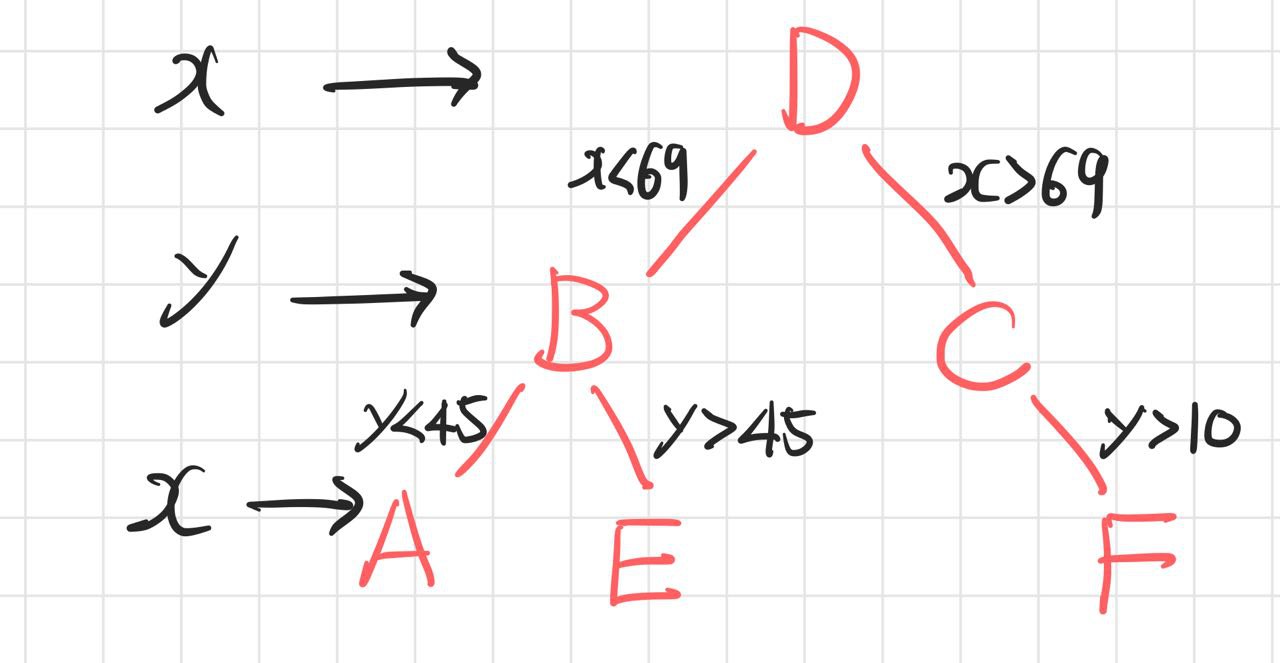
위 사진과는 조금 다른 모양의 트리가 되었는데, 트리를 무슨 기준으로 나누느냐에 따라 모양이 달라질 수 있다.
KD Tree의 핵심은 x->y->z->x->... 와 같이 각 축 별로 번갈아가면서 정렬하며 배열을 나눈다는 것이다.

출처: https://www.researchgate.net/figure/An-example-two-dimensional-k-d-tree-k-2-built-from-nodes-a-through-h-Dividing-planes_fig2_314298746

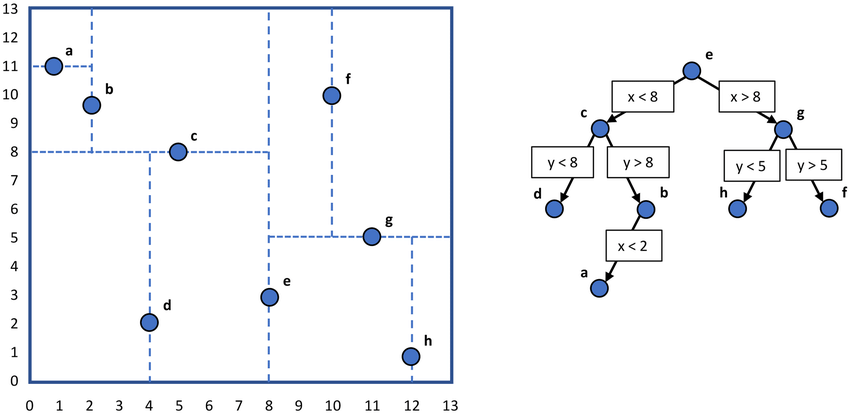
위 예시가 트리별로 중앙값을 나눈 예시이다.

KD Tree에서 가장 가까운 점 찾기

이제 예시로 (80, 75) 좌표가 주어졌을 때 어떻게 KD Tree를 이용해 가장 가까운 Point를 찾을 수 있는지 알아보자.

1. 새로운 점이 트리의 어디에 삽입 되어야 하는지 찾기

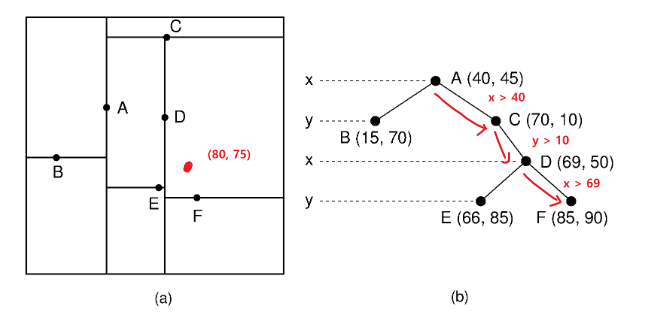
위와 같이 주어진 점과 부모 노드(중앙값)와의 비교를 통해 내려가면서 주어진 점이 어느 리프 노드에 위치하는지 찾는다.

2. 도달한 리프노드와의 거리를 반지름으로 원을 그려 침범하는 영역(브랜치)을 찾는다.

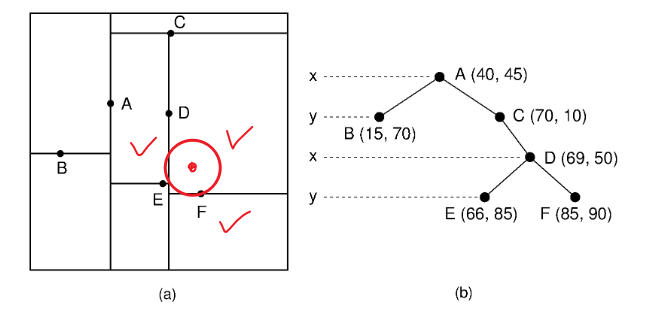
위 그림에서는 x < 69인 영역(브랜치)와의 비교가 추가로 필요하다.
만약 F가 리프노드가 아니라면 y > 90인 브랜와도 비교가 필요할 것이다.

이렇게 A ~ F 까지 모든 점을 순회하는게 아니라 일부의 점과 비교하면서 가장 가까운 점을 찾을 수 있게 되었다.

장단점

장점

• 구현이 단순하고 (차원수가 적을 때) 생성 비용이 낮다
• 근접 포인트를 찾는 문제에서 매우 효과적이다

단점

• 만약 Point 위치가 동적으로 변경된다면 처음부터 생성해야한다. (동적 업데이트에 불리)
• 트리구조가 불균형해질 수 있다.

즉 KD 트리는 포인트의 위치가 변하지 않고 계속 추가만 될 때 유리한 자료구조이다.

BVH

BVH는 Boundingbox Volume Hierarchy의 약자로
객체의 바운딩박스를 이용해 객체 Polygon을 트리 형태로 저장한 자료구조이다.

출처: https://developer.nvidia.com/blog/thinking-parallel-part-ii-tree-traversal-gpu/

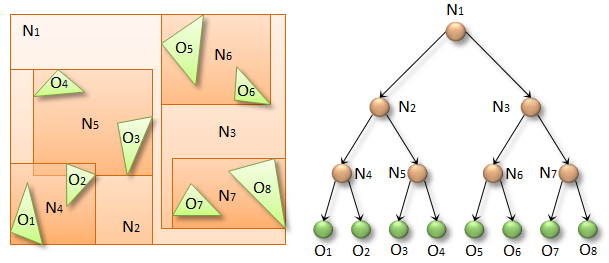
위 그림과 같이 모든 객체를 포괄하는 바운딩 박스부터 시작하여 더 작은 바운딩박스를 그리면서 객체가 리프 노드가 되도록 하는 방식이다.

KD Tree와 동일하게 트리를 나누는 여러가지 전략이 있으며, 가장 구현이 쉬운 것은 특정 축 방향으로 정렬한 뒤 중앙값을 기준으로 좌우로 나누는 방식이다.
위의 예제가 중앙값을 기준으로 나누는 방식을 채택했다.

다만 KD Tree와 달리 자식 노드의 개수가 2개가 아니어도 상관이 없다.
자식 노드의 개수가 많다면 각 노드당 비교해야하는 횟수는 늘어나지만, 깊이가 얕아진다는 장점이 있다.

BVH 생성

원리 자체는 KD Tree와 비슷하기 때문에 자세히 다루지는 않겠다.

다만 BVH의 경우 3D polygon 또는 다른 바운딩 박스로 부터 새로운 육면체 바운딩 박스를 계산해주어야 한다는 차이가 있다.

export const computeBounds = (
  triangleBounds: Float32Array,
  startIndex: number,
  count: number,
  target: Float32Array,
  centroidTarget: Float32Array | null = null
) => {
  initBounds(target);
  if (centroidTarget) initBounds(centroidTarget);
  const includeCentroid = !!centroidTarget;

  for (let i = startIndex, end = startIndex + count; i < end; i++) {
    const tri6 = i * 6;

    const xCenter = triangleBounds[tri6 + 0];
    const xDelta = triangleBounds[tri6 + 1];

    const yCenter = triangleBounds[tri6 + 2];
    const yDelta = triangleBounds[tri6 + 3];

    const zCenter = triangleBounds[tri6 + 4];
    const zDelta = triangleBounds[tri6 + 5];

    if (xCenter - xDelta < target[0]) target[0] = xCenter - xDelta;
    if (xCenter + xDelta > target[3]) target[3] = xCenter + xDelta;

    if (yCenter - yDelta < target[1]) target[1] = yCenter - yDelta;
    if (yCenter + yDelta > target[4]) target[4] = yCenter + yDelta;

    if (zCenter - zDelta < target[2]) target[2] = zCenter - zDelta;
    if (zCenter + zDelta > target[5]) target[5] = zCenter + zDelta;

    if (includeCentroid) {
      if (xCenter < centroidTarget[0]) centroidTarget[0] = xCenter;
      if (xCenter > centroidTarget[3]) centroidTarget[3] = xCenter;

      if (yCenter < centroidTarget[1]) centroidTarget[1] = yCenter;
      if (yCenter > centroidTarget[4]) centroidTarget[4] = yCenter;

      if (zCenter < centroidTarget[2]) centroidTarget[2] = zCenter;
      if (zCenter > centroidTarget[5]) centroidTarget[5] = zCenter;
    }
  }
};

대략 이런과정이 필요하다.

장단점

장점

• 객체가 움직여도 비교적 쉽게 트리를 갱신할 수 있다.
• 충돌 감지에 유리하다.

단점

• Cube에서 벗어난 형태의 객체일 수록 불리하다. (긴 꼬리를 가진 동물 등)
• KD Tree에 비해 더 많은 메모리가 필요하다. (최소 8의 길이를 갖는 bounding box를 이용하므로)

결론

다행히도 라이브러리가 잘 되어있기 때문에 트리를 생성 및 탐색하는 과정을 일일히 구현하지는 않아도 된다.

다만 원리를 알고쓰고 싶어서 따로 정리하게 되었다.