혼자 공부하는 컴퓨터 구조+운영체제 책을 바탕으로 공부한 내용입니다.
노션에 정리한 것을 그대로 옮겨온 것으로, 일부 글자가 깨질 수 있습니다.

고정 소수점과 부동 소수점

• 고정 소수점과 부동 소수점은 컴퓨터에서 실수를 표현하는 방법이다.

0. 소수 계산 방식

• 십진수 : 11.59375
• 우선 정수부분은 기존 이진수 변환처럼 1011 로 변환할 수 있다.
• 소수부분은 계속 2를 곱해주면서 자리 올림이 발생하면 1, 아니면 0으로 처리하고, 나머지가 남지 않을 때까지 반복하면 된다.

0.59375 * 2 = 1.1875 >> 1
0.1875 * 2 = 0.375 >> 0
0.375 * 2 = 0.75 >> 0
0.75 * 2 = 1.5 >> 1
0.5 * 2 = 1.0 >> 1

• 즉 11.59375를 이진수 변환하면 1011.10011이 된다.

1. 고정 소수점 (Fixed Point)

• 비트 상에서 소수점이 찍힐 위치를 미리 정해놓고 소수를 표현하는 방식
  • 앞서 구했던 1011.10011을 그대로 사용하고 여기에 부호 비트만 추가한다.
• 장점 : 정수부와 소수부가 나누어지기 때문에 단순하다.
• 단점 : 사용 비트 수 대비 표현 가능한 수의 범위가 적거나, 정밀도가 떨어진다.

2. 부동 소수점 (Floating Point)

• 부동이란 것은 움직이지 않는다는 것이 아니라, 부유하듯이 떠다닌다는 뜻이다.
• 지수의 값에 때라 소수점의 위치가 변하는 방식을 활용한 소수점 표현 방법이다.

IEEE float형 부동 소수점 방식

정규화

• 우선 부동 소수점으로 소수를 저장하기 위해서는 소수를 정규화 해야한다.
• 정규화 방법은 이진수 실수를 마치 고정 소수점 방식처럼 표현한다고 했을 때, 정수부의 값이 1이 될때 까지 비트를 오른쪽으로 shift 하는 것이다.
  • 이 때 shift를 한 횟수가 부동 소수점의 지수부가 되고, 소수점 오른쪽에 있는 숫자가 모두 가수부가 된다.

# 예시
1011.10011 -> 1.01110011 * (1 << 3)

bias

• 다음의 두 가지 경우를 보자

# 고정 소수점 -> 부동 소수점
1011.10011 -> 1.01110011 * (1 << 3)
0.00101110011 -> 1.01110011 * (1 << -3)

• 위의 경우는 지수부에 +3을 표현해야하고, 아래의 경우는 지수부에 -3을 표현해야 한다.
• 그런데 현재 지수부는 양수와 음수를 구분할 수 있는 방법이 없다!
  • 2의 보수를 사용한다고 하더라도, 여전히 3과 -253을, -3과 253을 구분할 방법이 없다.
• 지수부의 부호를 구분하기 위해 지수부 제일 앞자리 비트의 1과 0으로 양수와 음수를 구분한다.
  → bias
  - bias가 1일 때, 즉 지수부의 값이 128 ~ 255일 때 지수부가 양수임을 의미한다.
  - bias가 0일 때, 즉 지수부의 값이 0 ~ 127일 때 지수부가 음수임을 의미한다.

장단점

• 장점 : 표현 할 수 있는 수의 범위가 크기 때문에 현재 대부분의 시스템에서 활용중이다
• 단점 : 여전히 오차가 존재하며, 가수부가 $1 / 2^{n}$ 꼴로 정확히 표현되어야 정확한 소수를 표현할 수 있다.

패리티 비트 & 해밍코드

패리티 비트

• 정보 전달 과정에서 오류가 있었는지 검사하기 위해 추가하는 비트
• 보통 전달하고자 하는비트에 1비트를 더하여 전송한다.
• 짝수 패리티와 홀수 패리티가 있다.
  • 단점 오류의 개수가 홀수 가지일 때만 오류 여부를 확인할 수 있다.

짝수 패리티

• 전송되는 비트 중 1의 수가 짝수가 되도록 한다.
• 전송되는 7비트가 1001100일 경우
  • 1의 개수는 홀수이므로, 가장 뒤에 패리티 비트 1을 붙여 1의 개수가 짝수가 되도록 한다
  • 전송 비트 : 10011001

해밍 코드

• 데이터 전송시 1비트의 오류를 정정할 수 있는 자기 오류 정정 코드를 말한다.
• 패리티 비트만는 오류 검출기능만 있고, 오류 수정기능이 없기 때문에 사용한다.
• 패리티 비트를 바탕으로 1비트 오류를 정정할 곳을 찾아 수정할 수 있다.

오류 수정 방법

• 패리티 비트는 2의 n승 번째 자리에 위치한다. 이 자리에 있는 패리티 비트가 짝수인지, 홀수 인지 기준으로 오류 위치를 판별한다.

예시

• 8비트의 데이터를 전송하고자 할 때, 패리티 비트가 들어갈 수 있는 위치는 1, 2, 4, 8이다. 즉 전송 데이터 8비트에 패리티 비트 4비트를 추가하여 총 12비트의 코드(해밍 코드)가 전송된다.
• 규칙 : n번 패리티 비트는 자기 자신의 위치부터 n번째 비트까지 자신의 패리티 비트 범위에 포함하며, 이후 n비트씩 건너 뛰며 패리티 비트 범위를 지정한다.
  • 1번째 패리티 비트는 1, 3, 5, 7, 9, 11의 패리티 비트 범위를 갖는다.
  • 2번째 패리티 비트는 2, 3, 6, 7, 10, 11의 패리티 비트 범위를 갖는다.
• 예시 : 아래의 예시는 총 7비트로 구성된 해밍 코드이다. 짝수 패리티 비트이다.

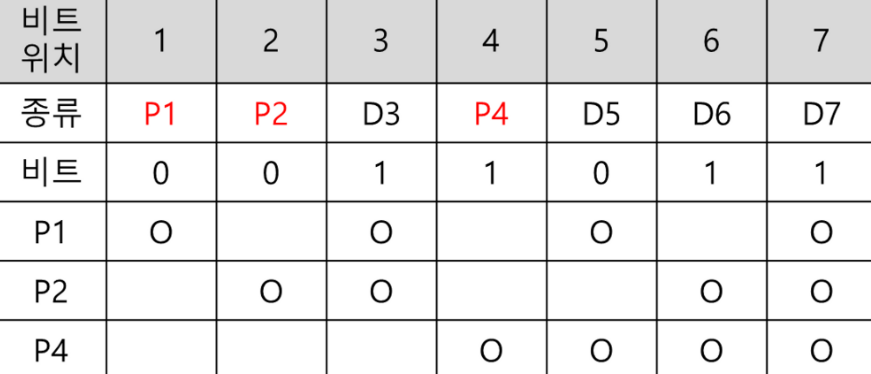
• P1 : 1,3,5,7에서 1의 개수는 2로 짝수이다 → ‘0’
• P2 : 2,3,6,7에서 1의 개수는 3으로 홀수이다 → ‘1’
• P4 : 4,5,6,7에서 1의 개수는 3으로 홀수이다 → ‘1’
• 역순으로 도출하면 신드롬 값은 110 이된다. 이는 십진수 6이므로, 6의 코드를 수정한다.
  • 신드롬 값이 0이면 오류가 없는 것이다.
• 오류 수정 후 비트 : 0011001

ARM 프로세서

프로세서란

• 메모리에 저장된 명령어들을 실행하는 유한 상태 오토마톤
  • 오토마톤 : 어떤 목적을 가지고 동작하는 기계장치를 추상화 한것
  • 유한 오토마톤 : 유한한 개수의 상태를 가지는 오토마톤
    • 상태 : 목적에 따라 설계된 상태를 말한다. 예를 들어 어떤 유한 오토마톤은 1과 0 단 2개의 상태를 가질 수 있다.
    • 유한 오토마톤은 임의의 시각 t에 단 하나만의 상태를 가질 수 있다.

ARM : Advanced RISC Machine

• ARM은 진보된 RISC 기기의 약자이다.
  • RISC는 명령어 집합 구조 중 하나이며, 적은 명령어 수와 1클럭 내외로 사용할 수 있는 명령어를 지향한다.

ARM의 시작

• 한 프로그래머가 대부분의 프로그램이 명령어 집합 중 작은 하위 집합만 사용한다는 것을 발견하고, 사용되지 않는 명령어를 제거한다면 칩의 전력과 공간을 절약할 수 있을 것이라 생각하여 이를 설계하는 프로젝트를 시작(RISC)

ARM 구조

• 아키텍처는 논리적인 명령 집합을 물리적으로 표현했기 때문에, 명령어가 복잡할수록 실제 물리적인 칩 구조도 크고 복잡해진다.
  • ARM은 RISC 기반이기 때문에 명령집합과 구조가 단순하다. 즉 ARM 기반 프로세서가 더 작고, 효율적이며 상대적으로 느리다.
• 명령 집합이 단순할 수록 적은 트랜지스터만 필요하기 때문에, 더 작은 크기를 가능하게 한다. 또한 트랜지스터가 적어 전력소모 역시 적다. 즉 스마트폰 및 태블릿을 위한 프로세서에 유리하다.

ARM vs x86

• x86 설계는 CPU와 GPU, 메모리, 보조기억장치 등이 별개로 구성되어있으며 손쉽게 교체가 가능한 반면, ARM은 CPU 코어와 PCI 등의 기타 하드웨어 기능이 동일한 물리 플랫폼에 있고, 다양한 기능이 내부 버스를 통해 한데 통합되어있다. 이렇게 구성 요소가 동일한 집적 회로에 배치되는 경우 이를 가리켜 SOC(System on a Chip)라고 한다.
• ARM은 칩의 기본 설계 구조를 만들 뿐, 실제 기능 추가 및 최적화는 개별 반도체 제조사의 영역이다. 때문에 물리적 설계는 같아도 사용하는 명령 집합이 달라 다른 칩이 될 수있다. 즉 하드웨어 설계자의 제어 권한이 더 커진다.

ARM의 장점

• ARM을 위해 개발된 프로세서는 오직 ARM 프로세서가 탑재된 기기에서만 실행할 수 있다.
  • ARM에서 실행되는 프로그램을 x86 프로세서에서 실행되게 하기 위해서는 프로그램을 수정해야한다.
  • 반면 ARM 기기에 동작하는 OS는 다른 ARM 기반 기기에서도 잘 동작한다. (안드로이드에 수많은 버전이 존재하는 이유)

현대 ARM

• 기술의 발달로 RISC와 CISC의 속도가 큰 차이가 나지 않게 되었다.
  • 클럭 속도는 전력 소모와 온도 조절에 달린 문제이기 때문에 현재 한계에 봉착한 상태
• 그런데 RISC의 명령어 길이가 일정하다는 특징이 명령어 병렬처리에 엄청난 이득을 발생시킨다는 것이 발견되었다 → 이를 통해 애플의 M1 칩이 Intel과 AMD 속도를 따라잡게 되었다.