강의 링크 : https://www.boostcourse.org/ai100/lecture/739177?isDesc=false

행렬

• 벡터 : 정수를 원소로 갖는 1차원 배열

• 행렬 : 벡터를 원소로 갖는 2차원 배열

• 파이썬의 numpy에서는 행 벡터가 기본 단위가 된다.

• 이때 행의 개수를 n개, 열의 개수를 m개라 하여 n x m행렬이라 한다.
  - 한개의 행 벡터는 m개의 성분(벡터)로 이루어져 있고

  • 행렬은 n개의 행 벡터로 이루여져 있다.

• 행렬의 각 성분은 행과 열이라는 인덱스로 나타낼 수 있다.

x = np.array([[1,-2,3],
			 [7,5,0],
             [-2,-1,2]])
x[2][0] # -2
x[1][1] # 5

• xij는 i행 j열에 있다는 뜻이다.

• 파이썬에는 x[i][j]로 참조할 수 있다.

• 행렬의 특정 행 또는 열을 고정하면 행(열)벡터라 부른다.

전치행렬(transpose matrix)

• 전치행렬은 행렬 X의 행과 열을 뒤바꾼 행렬을 말한다.
• X의 전치행렬은 T(transpose) 기호를 이용해 XT로 표시한다.

x = np.array([[1,2,3],
			  [4,5,6]])
xt = np.array([[1,4],
			   [2,5],
               [3,6]])

• X의 xij는 XT의 xji와 같다.

행렬의 이해

• 벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타낸다.
  - 각각의 행 벡터가 하나의 점을 나타냄
  • 행 벡터 xi는 i 번째 데이터를 의미

행렬의 연산

• 행렬은 벡터와 동일하게 같은 모양일 경우(m과 n이 같을 경우) 덧셈, 뺄셈이 가능하다.
• 행렬의 덧셈/뺄셈은 행렬의 두 성분을 모두 더한/뺀 것과 같다.

X ± Y = (xij ± yij)

• 성분곱 역시 벡터와 동일하게 계산할 수 있다.

X ◎ Y = (xij yij)
numpy에서는 ``로 연산한다

• 스칼라곱도 벡터와 동일하다.

aX = axij

행렬의 곱셈 (matrix multiplication)

• 행렬의 곱셈(행렬곱)은 벡터와 달리 왼쪽 행렬의 i번째 행벡터와 오른쪽 행렬의 j번째 열벡터 사이의 내적을 성분으로 갖는다.
• 즉 XY와 YX의 결과는 다르다. 행렬의 곱셈에서 순서는 매우 중요하다.
• 행렬곱을 위해서는 왼쪽 행렬의 행벡터 개수와, 오른쪽 행렬의 열벡터 개수가 같아야 한다.

XY = Σk(xik ykj)
numpy에서는 @로 연산한다.

x = np.array([[1,-2,3],
			 [7,5,0],
             [-2,-1,2]])
             
y = np.array([[-1,3],
			 [3,2],
             [-3,-1]])

위의 경우에서 Z = X @ Y라고 할 때
Z11 = (X11 * Y11) + (X12 * Y21) + (X13 * Y31) = (1 * 1) + (-2 * 3) + (3 * -3) = -14
Z12 = (X11 * Y12) + (X12 * Y22) + (X13 * Y32) = (1 * 3) + (-2 * 2) + (3 * -1) = -4
이와 같이 계산할 수 있다.

행렬의 내적

• numpy에서는 np.inner 함수를 통해 두 행렬의 내적을 구할 수 있다.
• 이때 numpy의 내적이란 왼쪽 행렬의 i번째 행벡터와, 오른쪽 행렬의 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 말한다.
  - 수학에서 말하는 내적과는 다르다는 것을 알아야 한다.
  • 즉 내적을 계산한 두 행렬의 행벡터 성분수가 같아야 한다.

XYT = Σk(xik yjk)

행렬과 데이터

행렬의 이해(2)

• 행렬은 벡터공간에서 두 벡터를 연결하는 일종의 연산자로 이해할 수 있다.
• x 벡터에 행렬곱 연산을 하는 것을 통해 다른 차원의 벡터 z로 보낼 수 있다.

x @ A = z
a11x1 + a12x2 + ... + a1mxm = z1
a21x1 + a22x2 + ... + a2mxm = z2

• 이러한 행렬곱을 통해 패턴을 추출하거나 데이터를 합축하는 등의 작업을 할 수 있다.
• 이렇게 한 점을 한 벡터공간에서 다른 벡터공간으로 이동시키는 이동 규칙을 선형변환(linear transform)이라 한다.

역행렬(inverse matrix)

• 역행렬은 행렬 A의 연산을 거꾸로 되돌려 항등행렬로 만드는 행렬이다.
• A-1으로 표기한다.
• 역행렬은 1. 행과 열의 숫자가 같은 n x n의 정방행렬이어야 한다 2. 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.

항등 행렬 : 행렬의 주대각선의 원소는 1이고 나머지는 모두 0인 행렬을 말한다. 임의의 행렬이나 벡터에 항등행렬을 곱하면 자기자신을 결과로 얻는다.

행렬식 : 간단히 말하면 n x n의 정방행렬이 갖고 있는 어떤 특정한 값을 나타내 주는 식이다.
2 x 2 행렬의 경우 ad - bc가 행렬식이다

• 역행렬은 행렬곱 순서와 상관없이 항등행렬이라는 같은 결과를 출력한다.

AA-1 = A-1A = I

numpy의 역행렬

• numpy가 제공하는 linalg(선형대수 함수) 라이브러리의 inv() 메소드를 통해 구할 수 있다.

x = np.array([[1,-2,3],
			 [7,5,0],
             [-2,-1,2]])
x_inv = np.linalg.inv(x) # x의 역행렬

• 단 컴퓨터의 부동소수점 연산이므로 x * x-1을 했을 때 정확히 0이 아닌, 0의 가까운 숫자가 계산된다.

유사역행렬(pseudo-inverse)

• 무어-펜로즈(Moore-Penrose) 역행렬이라고도 한다.
• 행과 열의 숫자가 다른 경우에도 계산할 수 있다.
• A+라 표기한다.
• 행의 개수가 많은지, 열의 개수가 많은지에 따라 계산 방법이 다르며, 역행렬과 달리 행렬곱 순서의 영향을 받는다.

n ≥ m (행이 열보다 많을 때)
A+ = (ATA)-1AT
A+A = I 만 성립한다. (순서가 바뀌면 성립하지 않음)

m ≥ n (열이 행보다 많을 때)
A+ = AT(AAT)-1
AA+ = I 만 성립한다.

numpy의 무어-펜로즈 역행렬

• linalg(선형대수 함수) 라이브러리의 pinv() 메소드를 통해 구할 수 있다.

무어-펜로즈 역행렬 응용1 : 연립방정식 풀기

• m ≥ n인 경우, 즉 변수의 개수가 식의 개수보다 많은 경우 연립방정식의 해를 구할 수 있다.

Ax = b
▼ 연립방정식 (m ≥ n)
a11x1 + a12x2 + ... + a1mxm = b1
a21x1 + a22x2 + ... + a2mxm = b2
...
an1x1 + an2x2 + ... + anmxm = bn

x = A+b = AT(AAT)-1b
x의 해를 하나 구할 수 있다.

무어-펜로즈 역행렬 응용2 : 선형회귀분석

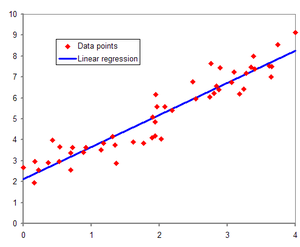
출처 : 위키백과

• n ≥ m인 경우(식이 변수보다 많은 경우) 데이터를 선형모델로 해석하는 선형회귀식을 구할 수 있다.
  - 여기서 식이 많다는 것은 데이터를 나타내는 점(=행벡터)가 벡터의 차원보다 더 많다는 것이다.

선형회귀식 : Xβ = y

• 식(데이터)이 매우 많기 때문에 모든 식을 만족하는 Xβ를 찾는 것은 불가능하다. (모든 데이터가 한 선 위에 있을때만 가능)
• 이때 L2-노름을 사용하여 식과 데이터 사이의 유클리드 거리가 최소가 되는 y hat 값을 찾을 수 있다.

Xβ = ŷ
β = X+ŷ = (XTX)-1XTŷ

• 파이썬에서는 sklearn의 LinearRegression 메소드를 이용할 수 있는데, 이것과 같은 결과를 가져 올 수 있다.

• 단 numpy의 linalg.pinv()를 이용할 때는 y절편을 고려하지 않았으므로, intercept항을 직접 추가해야한다.

사실 이부분은 잘 이해가 가지 않는다.
y절편이 필요하다는 것은 알겠지만, 어떻게 추가할 수 있다는 걸까?