블룸 필터
블룸 필터는 집합 내에 특정 원소가 이미 존재하는지 검사할 때 사용하는 메모리 효율적인 자료구조입니다.
랜덤한 해시값을 생성하는 유일 ID 생성기, 중복 요소 필터링 시스템에서 사용할 수 있습니다.
특징
- O(1)의 시간복잡도로 빠른 검사
- 원소 개수와 상관 없이 동일한 메모리를 사용 (메모리 효율적)
- 존재하지 않는 원소가 존재한다고 판단하는 False Positive의 위험 존재, 원소 개수가 많아질수록 False Positive 위험 증가
- 원소의 추가는 자유롭지만, 원소를 삭제하는 것이 불가능
알고리즘

블룸 필터는 크기 M의 비트 어레이로 표현할 수 있습니다.
여기서는 M = 8로 가정하겠습니다.

x라는 원소를 블룸 필터에 추가하기 위해서는 원소를 특정 값으로 맵핑하는 해시 함수가 1개 이상 필요합니다.

위 그림처럼 해시 함수의 값으로 {1, 5}가 주어졌다면 비트 어레이의 1번 인덱스와 5번 인덱스를 1로 할당하면 블룸 필터에 x가 추가된 것입니다.
동일한 해시 함수를 사용한다면 x의 해시 값은 언제나 동일할 것이므로, 블룸 필터에서 해시 값에 해당하는 인덱스가 모두 1이라면 해당 원소는 이미 블룸 필터에 존재하는 것으로 판정합니다.


이어서 y 원소를 추가할 때 다음과 같은 과정을 거칩니다.
y를 해싱하여 해시 값{3, 6}획득- 해시값에 해당하는 인덱스의 비트가 모두 1인지 확인
- 모두 1이 아니므로,
y가 블룸 필터에 존재하지 않는 원소라고 판정 y의 해시값에 해당하는 인덱스의 비트를 모두 1로 수정 (y를 블룸 필터에 추가)

그런데 원소 z의 해시 함수의 결과가 위와 같이 {1, 6}이 나온다면, 블룸 필터에서 해당 하는 비트가 모두 1이 되어 z가 이미 블룸 필터에 존재한다고 판정 해버립니다.
이것이 앞서 설명한 False Positive 위험이 존재한다는 것입니다. 자연스럽게 원소가 많이 추가될 수록 False Positive 위험이 증가한다는 것도 알 수 있습니다.
False Positive 완화하기
False Positive의 발생을 완화하기 위해 가장 직관적인 방법으로는 M을 크게 하는 방법이 있습니다.
다만 M을 크게 할수록 블룸 필터를 저장하기 위한 메모리가 증증가한다는 문제가 있습니다.
또 하나의 방법으로는 여러 종류의 해시 함수 K개를 동시에 사용하는 것입니다.
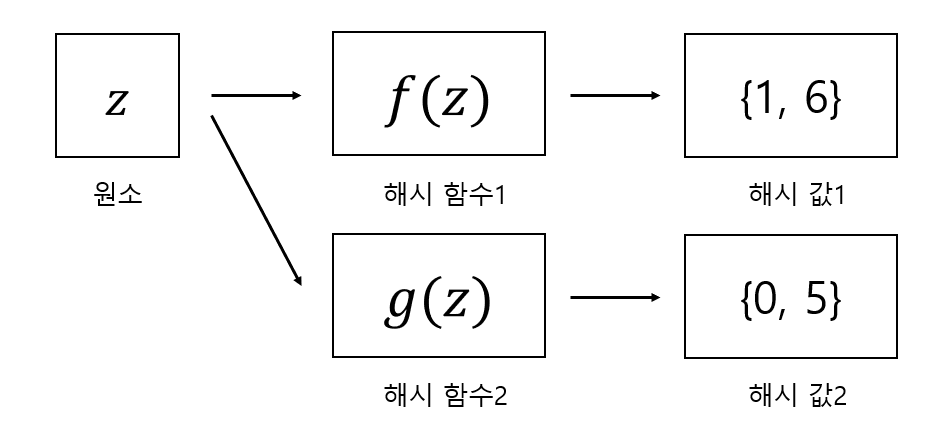
예를 들어 위 그림처럼 K = 2로 해시 함수를 하나 더 두어, 모든 해시 값에 대해 블룸 필터의 비트가 1인지 검사할 수 있습니다. 이를 통해 False Positive가 발생할 확률을 낮출 수 있습니다.
이 경우 z를 저장하기 위해서는 {0, 1, 5, 6}의 비트를 모두 1로 수정해야 합니다.
다만 이 방법은 해시 함수 및 검사 횟수가 증가하여 연산 비용이 커지고, 원소 하나를 저장하기 위해 더 큰 블룸 필터가 필요합니다.
이렇듯 False Positive의 발생 확률과 메모리/시간 효율은 Trade Off 관계에 있습니다.
최적의 M, K 찾기
블룸 필터는 다양한 방법으로 구현이 가능합니다.
지금까지는 설명을 위해 해시 함수가 두 개의 값을 출력했지만, 일반적으로 하나의 값으로 맵핑하는 해시 함수를 여러 종류 사용하는 것 같습니다.
이 경우 각 원소를 해싱하는 것은 독립 시행이기 때문에, n개의 원소가 추가되어 있는 블룸 필터에 새로운 원소를 추가하려 할 때 False Positive가 발생할 확률을 계산할 수 있습니다. 이 부분은 수학이라 따로 자세히 공부하지는 않았습니다.
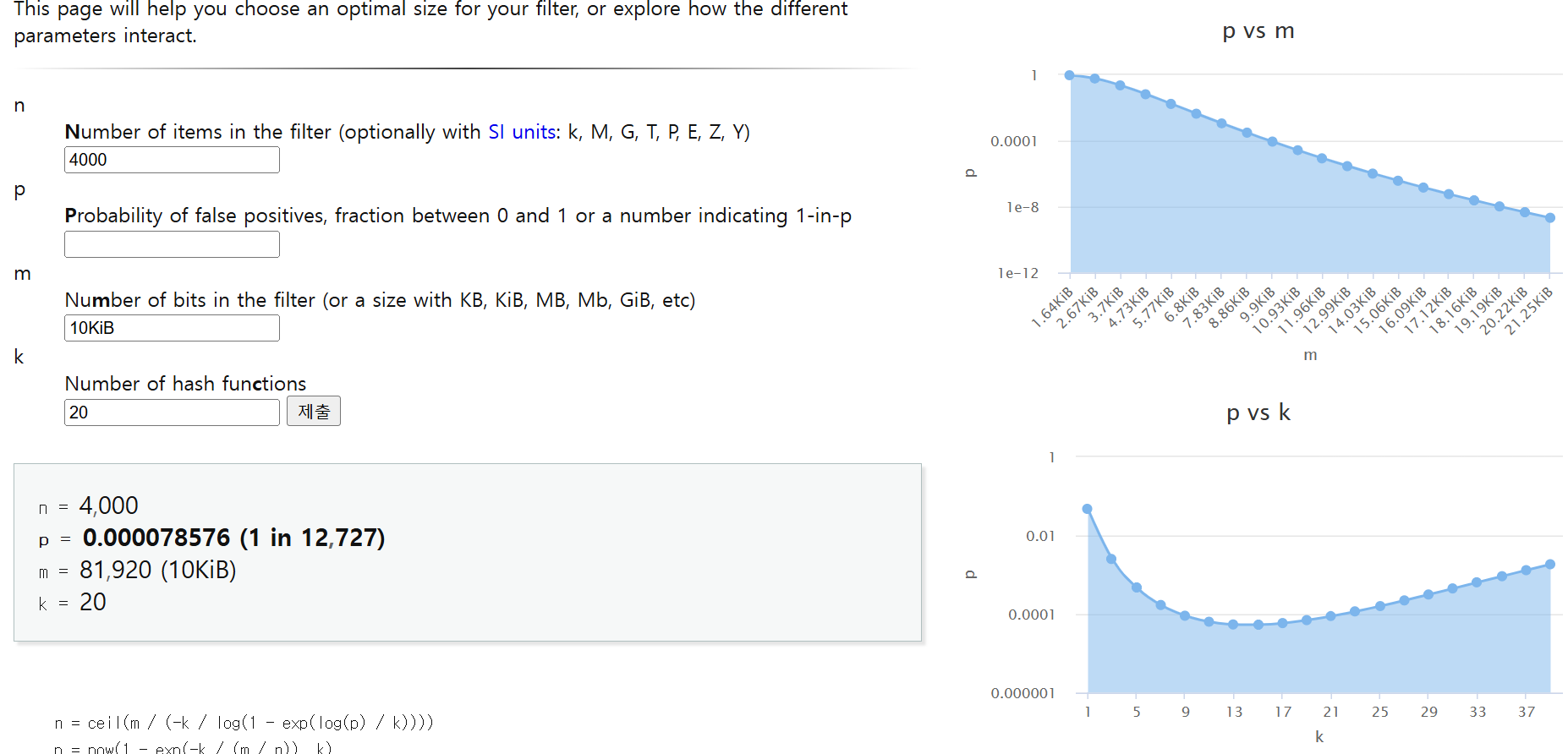
이 웹사이트에서 직접 변수를 넣어 계산해볼 수 있습니다.
예를 들어 블룸 필터의 비트 어레이 길이가 81,920(10KiB)이고, 해시 함수 20 종류를 사용하는 블룸 필터에서, 4001번째 원소를 추가할 때 False Positive가 발생할 확률은 약 0.008%입니다.
또한 M이 고정되어 있다면 미분을 활용해서 최적의 K값을 찾을 수 있습니다. 저는 K = 20을 넣었지만, 사이트에서는 K = 15일 때 최적값이라고 하네요.
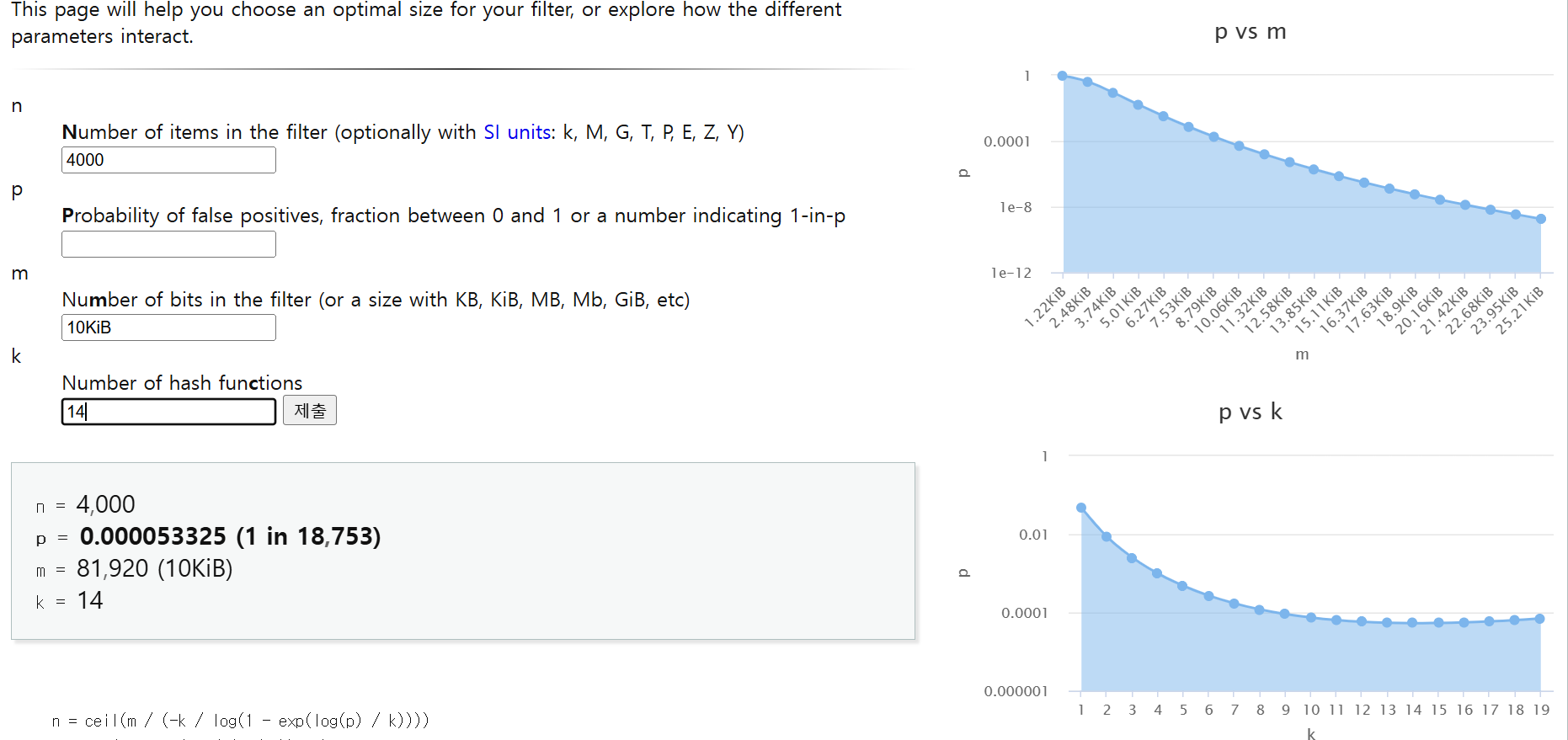
실제로 K = 14로 변경해보니 확률이 약 0.005%로 감소했습니다. 이 경우 연산 비용도 줄일 수 있으니 일석이조네요 :)

