[three.js] Geometry 종류

cjkangme·2023년 10월 29일
three.js

three-js

목록 보기
2/8

참고 강의 : GIS Developer 유튜브 강의

three.js의 BufferGeometry는 배열 형태로 3차원 오브젝트를 구성하는 정점의 정보와 인덱스 정보 등을 저장함으로써 3차원 구조체의 형상을 정의한다.

three.js는BufferGeometry를 확장한 다양한 형상의 지오메트리를 제공하는데, 이를 이용해 여러 종류의 도형을 쉽게 그릴 수 있다.

BufferAttribute

BufferGeometry의 속성들을 알아보자.

  • 정점 위치 : 각 정점의 x, y, z 축에 대한 위치 좌표
  • 정점 인덱스 : 정점에 대한 인덱스, 이를 이용해 정점을 3개씩 묶으면 3차원 객체를 구성하는 삼각형 폴리곤을 알 수 있다.
  • 수직 벡터 : 각 정점의 표면 법선 벡터
  • 정점 색상 : 각 정점에 적용되는 색상
  • UV 좌표 : 3차원 객체에 텍스쳐를 씌울 때 텍스쳐에 맵핑되는 좌표
  • 그 외 사용자 정의 데이터

three.js가 제공하는 지오메트리

BoxGeometry 공식 문서
사실 모든 속성은 공식 문서가 제공하는 예제로 직접 다뤄보는 것이 더 익히기 쉽다.

BoxGeometry

new BoxGeometry(width?: number, height?: number, depth?: number, widthSegments?: number, heightSegments?: number, depthSegments?: number): THREE.BoxGeometry

가로, 세로, 깊이(높이)로 구성된 육면체 지오메트리

  • width : 가로 (기본값: 1)
  • height : 세로 (기본값: 1)
  • depth : 깊이 (기본값: 1)
  • widthSegments, heightSegments, depthSegments : 각 방향에 대한 분할 수 (기본값: 1)
const geometry = new THREE.BoxGeometry(1, 1, 1, 2, 2, 2);

각 방향으로 모두 2등분한 육면체가 생성된다.

CircleGeometry

CircleGeometry(radius : Float, segments : Integer, thetaStart : Float, thetaLength : Float)

2D 원 모양의 Geometry

  • radius : 원의 반지름 (기본값: 1)
  • segments : 원의 분할 수 (기본값: 32, 최솟값 : 3)
    • 완전한 원을 그리는 것이 아니라, 분할 수 만큼의 삼각형을 그려 원을 표현한다. (기본적으로 모든 Geometry는 이렇게 동작)
    • Segments가 클 수록 원 모양에 가까워진다. 최솟값인 3의 경우 삼각형이 표현된다.
  • thetaStart : 원의 시작 각도, 라디안 단위 (기본값: 0)
  • thetaLength : 원의 연장 각도, 라디안 단위 (기본값: 2 * PI)
const geometry = new THREE.CircleGeometry(1, 8, Math.PI, Math.PI / 2);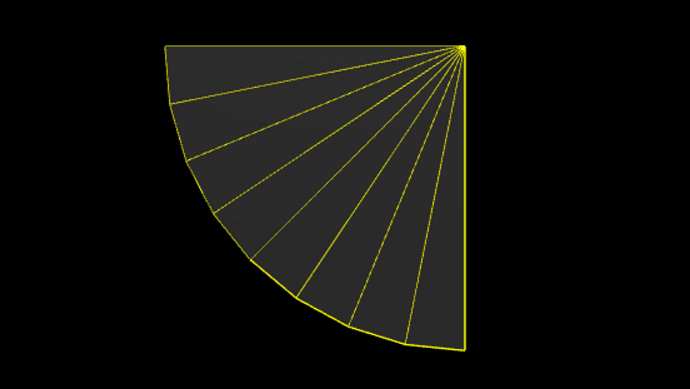

180도 방향에서 시작해 1/4만큼의 원을 8개의 도형으로 그린 원이 생성된다.

ConeGeometry

ConeGeometry(radius : Float, height : Float, radialSegments : Integer, heightSegments : Integer, openEnded : Boolean, thetaStart : Float, thetaLength : Float)

3차원 원뿔 모양의 Geometry

  • radius: 밑면의 반지름 (기본값: 1)
  • height: 원뿔의 높이 (기본값: 1)
  • radialSegmnents: 밑면 둘레 방향의 분할 수 (기본값: 32)
    • 3보다 적은 값을 줄 수 있지만, 2를 주면 2D 삼각형, 1을 주면 선이 되어버린다.
  • heightSegments: 원뿔 높이 방향의 분할 수 (기본값: 1)
  • openEnded: 밑면이 막혀있는지 여부 (기본값: false)
  • thetaStart: 원뿔의 시작값 (기본값: 0)
  • thetaLength: 원뿔의 연장값 (기본값: 2 * PI)

CylinderGeometry

CylinderGeometry(radiusTop : Float, radiusBottom : Float, height : Float, radialSegments : Integer, heightSegments : Integer, openEnded : Boolean, thetaStart : Float, thetaLength : Float)

3차원 원기둥 모양의 Geometry

  • radiusTop: 윗면의 반지름 크기 (기본값: 1)
  • radiusBottom: 밑면의 반지름 크기 (기본값: 1)
  • height: 원통의 높이 (기본값: 1)
  • radialSegments: 밑면 둘레 방향 분할 수 (기본값: 32)
  • heightSegments: 원뿔 높이 방향의 분할 수 (기본값: 1)
  • openEnded: 밑면이 막혀있는지 여부 (기본값: false)
  • thetaStart: 원기둥의 시작 각도 (기본값: 0)
  • thetaLength: 원기둥의 연장 각도 (기본값: 2 * PI)

SphereGeometry

SphereGeometry(radius : Float, widthSegments : Integer, heightSegments : Integer, phiStart : Float, phiLength : Float, thetaStart : Float, thetaLength : Float)

3차원 구 형태의 Geometry

  • radius: 구의 반지름 크기 (기본값: 1)
  • widthSegments: 수평 방향 분할 수 (기본값: 32, 최솟값: 3)
    • CircleGeometry의 segments와 동일한 역할
  • heightSegments: 높이 방향 분할 수 (기본값: 16, 최솟값: 2)
  • phiStart: 수평 방향의 시작 각도 (기본값: 0)
  • phiLength: 수평 방향의 연장 각도, 2PI일 때 완전한 구를 이룸 (기본값: 2 PI)
  • thetaStart: 수직 방향의 시작 각도 (기본값: 0)
  • thetaLength: 수직 방향의 연장 각도, PI일 때 완전한 구를 이룸 (기본값: PI)

RingGeometry

RingGeometry(innerRadius : Float, outerRadius : Float, thetaSegments : Integer, phiSegments : Integer, thetaStart : Float, thetaLength : Float)

2차원 도넛 모양의 Geometry

  • innerRadius: 내부 원의 반지름 크기 (기본값: 0.5)
  • outerRadius: 외부 원의 반지름 크기 (기본값: 1)
  • thetaSegments: 링을 나타내는 분할 수 (기본값: 32, 최솟값: 3)
  • phiSegments: 링의 둘레를 나누는 분할 수 (기본값: 1, 최솟값: 1)
  • thetaStart: 시작 각도 (기본값: 0)
  • thetaLength: 연장 각도 (기본값: 2 * PI)
const geometry = new THREE.RingGeometry(0.5, 1, 8, 3);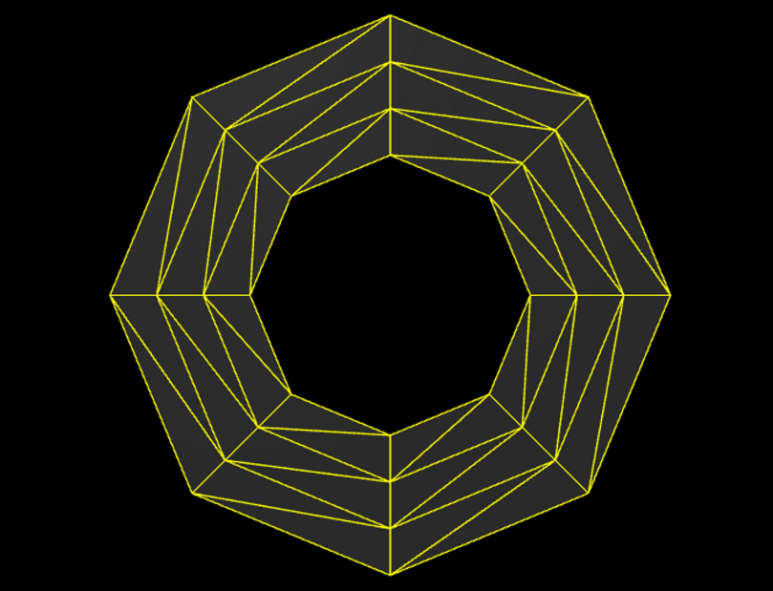

8개의 thetaSegments를 통해 팔각형의 링이 형성되고, 둘레 방향으로 3분할 되었다.

PlaneGeometry

PlaneGeometry(width : Float, height : Float, widthSegments : Integer, heightSegments : Integer)

2차원 사각 평면 모양의 Geometry

  • width: 너비 (기본값: 1)
  • height: 높이 (기본값: 1)
  • widthSegments: 너비 방향의 분할 수 (기본값: 1)
  • heightsSegments: 높이 방향의 분할 수 (기본값: 1)

TorusGeometry

TorusGeometry(radius : Float, tube : Float, radialSegments : Integer, tubularSegments : Integer, arc : Float)

3차원 도넛 모양의 Geometry

※ Torus의 형상을 나타내는 닫힌 원기둥 링을 tube라고 한다.

  • radius: Torus 중심으로부터 tube의 중심까지의 거리 (기본값: 1)
  • tube: tube의 반지름 크기 (기본값: 0.4)
    클수록 내부 빈공간이 적은 뚱뚱한 Torus가 만들어진다.
  • radialSegments: Torus 방사 방향의 분할 수 (기본값: 12)
  • tubularSegments: Torus 원 방향의 분할 수 (기본값: 48)
  • arc : Torus의 연장 각도, 2 PI일 때 완성된 도넛이 됨 (기본값: 2 PI)
const geometry = new THREE.TorusGeometry(1, 0.4, 12, 8);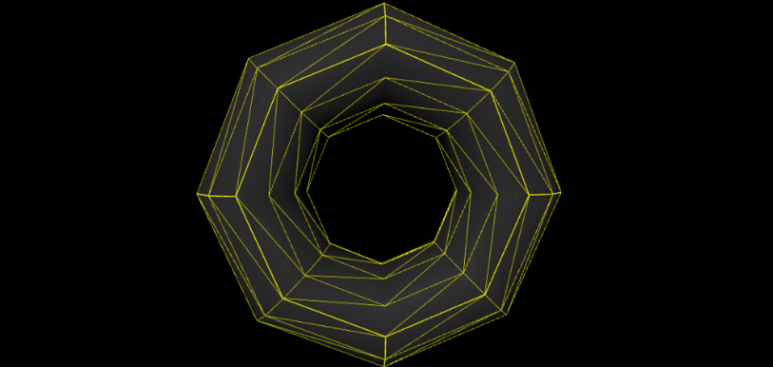

radialSegments = 12이므로 tube가 12분할 되었다, tubularSegments = 8이므로 원 형상은 팔각형이 되었다.

ShapeGeometry

2차원 도형의 모양을 정의하는 THREE.Shape 인스턴스를 통해 2차원 도형을 나타내는 Geometry

Shape 인스턴스를 생성하고, 메서드를 통해 직선 및 다양한 모양의 곡선을 통해 도형을 그릴 수 있다. (python의 turtle과 유사한 방식)

const shape = new THREE.Shape();
    shape.moveTo(1, 1);
    shape.lineTo(1, -1);
    shape.lineTo(-1, -1);
    shape.lineTo(-1, 1);
    shape.closePath(); // 도형 닫기

정사각형이 그려졌다.

이렇게 생성한 THREE.Shape 인스턴스를 ShapeGeometry로 감싸면 Mesh 형태로 표현할 수 있다.

TubeGeometry

TubeGeometry(path : Curve, tubularSegments : Integer, radius : Float, radialSegments : Integer, closed : Boolean)

어떤 곡선을 따르는 tube를 나타내는 Geometry

곡선을 정의하는 THREE.Curve 인스턴스를 통해 다양한 모양의 tube를 그릴 수 있다.

  • path : THREE.Curve 객체
  • tubularSegments: tube의 분할 수 (기본값: 64)
    THREE.Curve에서 getPoints로 곡선을 표현하는 Points 수를 설정하는 것과 유사하다.
  • radius : tube의 반지름 (기본값: 1)
  • radialSegments: tube의 원통을 표현하는 분할 수 (기본값: 8)
    예를들어 값을 4를 주면 원기둥 튜브가 아닌 사각기둥 튜브가 된다.
  • closed: 곡선을 닿힌 형태인지 아닌지 결정 (기본값: false)
    true를 주면 양 곡선의 끝단이 연결된다.

LatheGeometry

LatheGeometry(points : Array, segments : Integer, [param:Float phiStart], phiLength : Float)

어떤 선을 y축 방향으로 회전시킴으로써 얻어지는 3차원 도형을 나타내는 Geometry

  • points: 기준이 될 선을 그리는 point 배열
    각 point를 잇는 선을 통해 직선 또는 곡선을 표현 가능
  • segments: 회전체의 분할 수 (기본값: 12)
  • phiStart: 회전체 시작 각도, 0일 때 3시방향 (기본값: 0)
  • phiLenght: 회전체 연장 각도, 2 PI일 때 완전히 닫힌 회전체가 됨 (기본값: 2 PI)

ExtrudeGeometry

ExtrudeGeometry(shapes : Array, options : Object)

THREE.Shape로 표현된 2차원 도형에 깊이 값을 정의하여 3차원 구조체를 나타내고, 밑면을 비스듬하게 처리할 수 있는 Geometry

※ 비스듬하게 처리하는 것을 beveling이라고 한다.

  • shapes: Three.Shape 객체를 통해 나타낼 평면
  • options: ExtrudeGeometry를 그리는 옵션
    • steps: 깊이 방향으로의 분할 수 (기본값: 1)
    • depth: 깊이값, 클수록 구조체의 높이가 커짐 (기본값: 1)
    • bevelEnabled: beveling 처리를 할 것인지 여부 (기본값: true)
    • bevelThickness: bevel의 두께, 클 수록 비스듬한 면적이 커짐 (기본값: 0.2)
    • bevelSize: Shape의 외각선으로부터 얼마나 멀리 beveling을 할 것인지, 클수록 구조체가 뚱뚱해짐 (기본값: bevelThickness - 0.1)
    • bevelSegments: beveling 단계 수, 클 수록 bevel이 곡선 형태를 띔 (기본값: 3)
    • extrudePath: THREE.Curve가 값으로 들어가야 하며shapes에서 정의된 모양이 연장될(extruded) 곡선 모양을 결정한다.

TubeGeometry와 같이 곡선 등 비정형의 3차원 객체를 표현해야할 때, Three.Shape객체와 extrudePath 옵션을 통해 path를 따라 다양한 모양의 3차원 객체를 그려낼 수 있다.

TextGeometry

텍스트를 3D 객체로 나타내는 Geometry

ExtrudeGeometry의 파생 클래스이며, core에는 탑재되어있지 않아 별도로 불러와야 하는 애드온이다.

사용하기 위해 json 폰트 파일과 FontLoader 클래스를 통해 json을 THREE.Font 인스턴스로 변환해야 한다.

TextGeometry(text : String, parameters : Object)

  • text: 나타낼 텍스트
  • parameters: text를 나타내기 위한 설정 값
    • font: THREE.Font 인스턴스
    • size: 텍스트의 크기 (기본값: 100)
    • height: 텍스트의 두께(높이) (기본값: 50)
    • curveSegments: 글자를 나타내는 분할 수 (기본값: 12)

그 외 파라미터는 bevel 관련 설정이며 ExtrudeGeometry의 옵션 값을 동일하게 사용가능하다.

// 공식문서 예제
const loader = new FontLoader();

loader.load( 'fonts/helvetiker_regular.typeface.json', function ( font ) {

	const geometry = new TextGeometry( 'Hello three.js!', {
		font: font,
		size: 80,
		height: 5,
		curveSegments: 12,
		bevelEnabled: true,
		bevelThickness: 10,
		bevelSize: 8,
		bevelOffset: 0,
		bevelSegments: 5
	} );
} );
profile
cjkangme
이전 포스트

[three.js] three.js의 기본 구성 요소

다음 포스트

[three.js] Scene Graph

0개의 댓글