[백준] 1062. 가르침 (파이썬)

cjkangme·2023년 5월 27일

백준 비트마스크 알고리즘

Algorithm

목록 보기

23/35

문제 : https://www.acmicpc.net/problem/1062

문제 요약

N개의 단어가 주어진다.
26개의 알파벳 중 K개의 알파벳만을 가르쳐서 최대한 많은 단어를 읽을 수 있도록 해야한다.
모든 단어의 시작은 anta, 끝은 tica로 끝나므로, [a, c, i, n, t] 5개의 단어는 반드시 가르쳐야 한다.

예제

N=3 K=6
antarctica
antahellotica
antacartica

a, c, i, n, t에 더해서 r을 가르친다면 antarctica, antacartica 2개를 읽을 수 있다.
나머지 경우의 수는 아무 단어도 읽을 수 없다.

따라서 답은 2가 된다.

풀이

단어를 비트로 변환

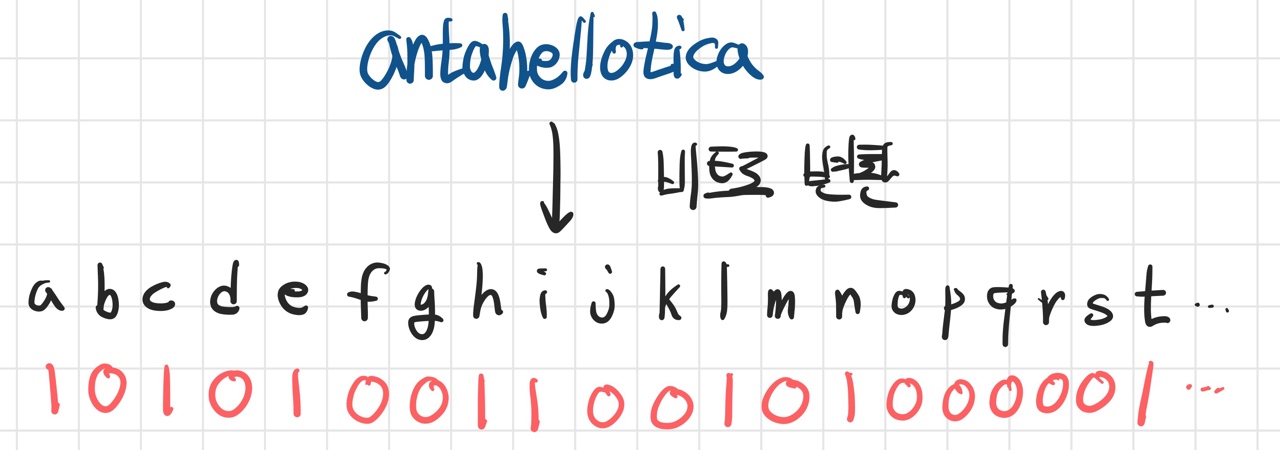(실제로는 z, y, x ... , d, c, b, a 의 역순 비트이다.)

위 그림과 같이 단어를 비트로 변환하여 가르친 알파벳과 & 연산을 함으로써 단어를 읽을 수 있는지 없는지 여부를 판단할 수 있다.

# 단어를 비트로 변환하는 함수
def word2bit(word):
    bit = 0
    for char in word:
        bit = bit | (1 << ord(char) - ord('a'))
    return bit

예를 들어 acint라는 단어가 주어졌을 때
a -> 0, c -> 2, i -> 8, n -> 13, t -> 19로 각각 변환하여 left shift 연산을 통해 비트를 만들어낸다.

acint는 000000010000010000100000101 = 532741로 변환된다.

조합

이제 알파벳을 가르칠 수 있는 경우의 수(조합)을 구해야 한다.
파이썬에서는 itertools 라이브러리의 combinations 함수를 사용해 쉽게 구할 수 있다.

# 가르칠 수 있는 알파벳 조합
base_bit = word2bit('acint')
alphabet = [1 << i for i in range(26) if not (base_bit & 1 << i)]

answer = 0
for combination in combinations(alphabet, K-5):
    know_bit = sum(combination) | base_bit

a, c, i, n, t는 반드시 가르쳐야하는 단어 조합이므로, 5개의 알파벳을 제외한 나머지 단어에서 조합을 구한다.

0 ~ 25까지의 범위에서 반복문을 돌고, 반드시 가르쳐야 하는 단어 조합(base_bit)이 아닌 알파벳의 비트를 alphabet 리스트에 추가해준다.

구해진 알파벳 리스트를 출력하면 다음과 같다.

[2, 8, 16, 32, 64, 128, 512, 1024, 2048, 4096, 16384, 32768, 65536, 131072, 262144, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432]
['0b10', '0b1000', '0b10000', '0b100000', '0b1000000', '0b10000000', '0b1000000000', '0b10000000000', '0b100000000000', '0b1000000000000', '0b100000000000000', '0b1000000000000000', '0b10000000000000000', '0b100000000000000000', '0b1000000000000000000', '0b100000000000000000000', '0b1000000000000000000000', '0b10000000000000000000000', '0b100000000000000000000000', '0b1000000000000000000000000', '0b10000000000000000000000000']

이어서 combinations 함수를 사용해 모든 경우의 수에 대해 반복문을 수행한다.
이미 이미 알고있는 단어를 합쳐야 하므로, | 비트 연산을 통해 하나의 비트로 만든다.

읽을 수 있는 단어 구하기

count = 0
for bit in bits:
    if bit & know_bit == bit:
		count += 1

bit는 주어진 단어, know_bit는 읽을 수 있는 알파벳을 의미한다.
만약 단어에 있는 알파벳을 모두 읽을 수 있다면, & 연산 결과가 변하지 않아야 한다.
만약 읽을 수 없는 알파벳이 있다면 & 연산으로 해당 비트 부분이 0이 되어 값이 변할 것이다.

위와 같은 원리로 읽을 수 있는 단어와 읽을 수 없는 단어를 구분할 수 있다.

단어를 읽을 수 있다면 count를 1 증가시키고, 모든 경우에 수에 대해 count의 최대값을 구하면 답을 구할 수 있다.

코드

import sys
from itertools import combinations

input = sys.stdin.readline

def word2bit(word):
    bit = 0
    for char in word:
        bit = bit | (1 << ord(char) - ord('a'))
    return bit

N, K = map(int, input().split())
words = [input().rstrip() for _ in range(N)]
bits = list(map(word2bit, words))
base_bit = word2bit('antic')

if K < 5:
    print(0)
else:
    alphabet = [1 << i for i in range(26) if not (base_bit & 1 << i)]
    answer = 0
    for combination in combinations(alphabet, K-5):
        know_bit = sum(combination) | base_bit
        count = 0
        for bit in bits:
            if bit & know_bit == bit:
                count += 1
        answer = max(answer, count)
    print(answer)