[백준] 1285. 동전 뒤집기 (파이썬)

cjkangme·2023년 3월 11일

python 백준 알고리즘

Algorithm

목록 보기

16/35

문제 : https://www.acmicpc.net/problem/1285

풀이

모든 경우의 수를 따지면서 뒷면으로 된 동전의 최소값을 찾는 문제이다.
비트마스킹을 활용하면 비교적 간편하게 모든 경우의 수를 확인할 수 있다.

1. 행 뒤집기

백준 문제에 업로드 되어있는 그림이다. 위쪽부터 순서대로 1, 2, 3행이라 했을 때 행을 뒤집을 수 있는 경우의 수는 다음과 같다.

하나도 뒤집지 않는다.
1행만 뒤집는다.
2행만 뒤집는다.
3행만 뒤집는다.
1행, 2행을 뒤집는다.
1행, 3행을 뒤집는다.
2행, 3행을 뒤집는다.
모두 뒤집는다.

즉 경우의수는 2^n개가 됨을 알 수 있으며, 이를 비트마스크로 간편하게 할 수 있다.
비트마스크를 모른다면 아래 게시글을 참조하자

14391. 종이 조각 (파이썬)

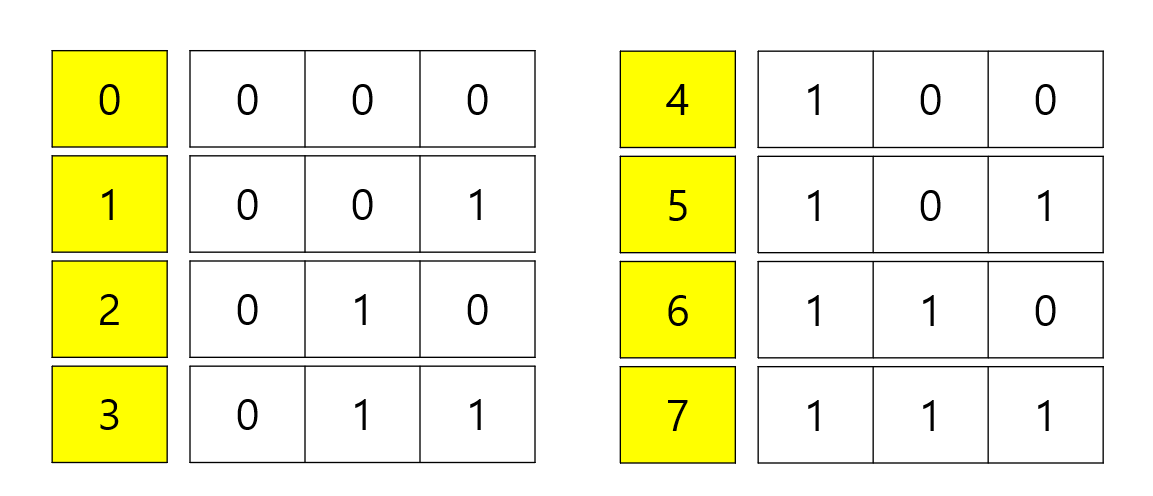
위 이진수 표에서 1일 때 행을 뒤집고, 0일 때 행을 뒤집지 않는 것으로 표현하면 모든 경우의 수를 확인할 수 있다.
즉 range(2 ** N) 또는 range(1 << N)을 통해 모든 경우의 수를 확인할 수 있다.

2. 열을 확인하며 개수 세기

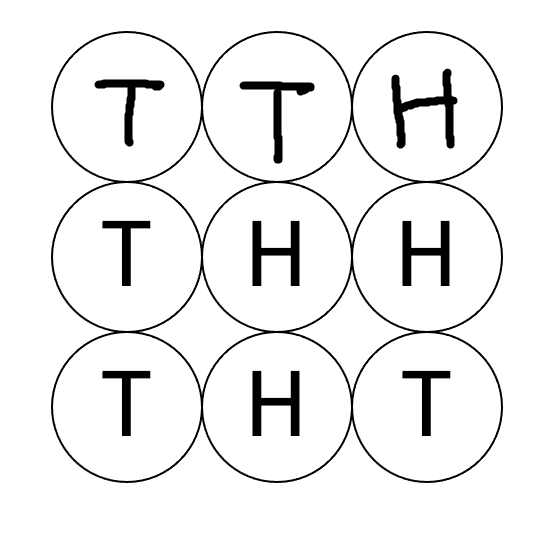
위 그림은 첫 그림에서 첫번째 행을 뒤집은 경우이다.
이제 각 열에대해 for loop을 돌면서 해당 열을 뒤집었을 때와 뒤집지 않았을 때 각각의 뒷면 수를 세어 최소값을 구하면 된다.

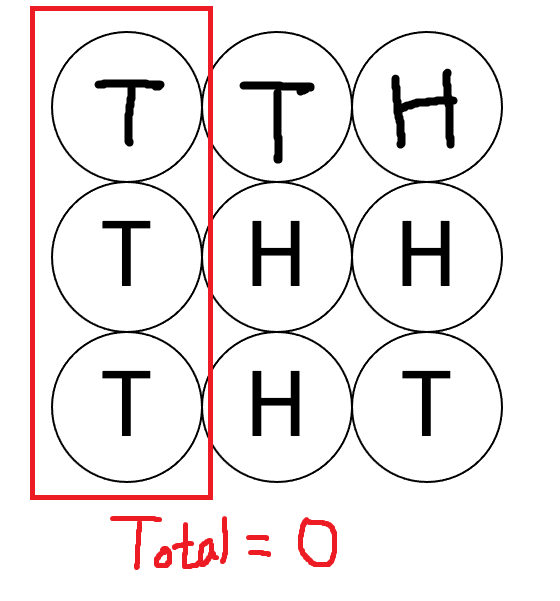
먼저 첫번째 열에서 뒷면의 개수는 3개이다. 만약 이 열을 뒤집는 다면 뒷면의 개수는 N-3 = 0개가 될 것이다.
최소값은 0이므로 Total은 여전히 0이다.

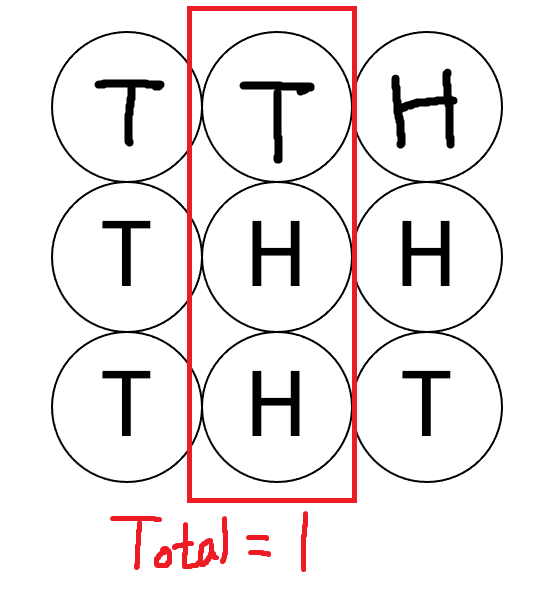
두번째 열에서는 뒷면의 개수는 1개, 뒤집는다면 N-1 = 2개이다.
최소값은 1이므로 Total = 0 + 1 = 1이된다.

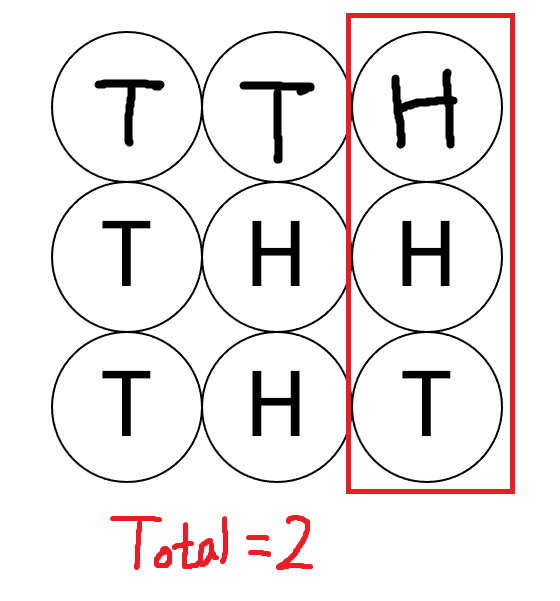
마지막 열에서는 뒷면의 개수는 1개, 뒤집는다면 N-1 = 2개이다.
최소값은 1이므로 Total = 1 + 1 = 2가된다.

이런식로 모든 경우의 수에 대해 Total을 구하면, 그 최소값이 정답이 된다.

코드

import sys
input = sys.stdin.readline

N = int(input())
board = [list(map(str, input().rstrip())) for _ in range(N)]

answer = 2147000000

# 1. 행이 뒤집힌 배열 생성
board_reversed = [["H"] * N for _ in range(N)]
for i in range(N):
    for j in range(N):
        if board_reversed[i][j] == board[i][j]:
            board_reversed[i][j] = "T"
# 2. 비트마스크로 경우의 수 탐색
for case in range(1 << N):
    board_temp = []
    for i in range(N):
        if case & (1 << i):
            board_temp.append(board_reversed[i])
        else:
            board_temp.append(board[i])
    # 3. 열방향 탐색으로 뒤집는 것과 안뒤집는 것중 최대값 저장
    total_count = 0
    for j in range(N):
        count = 0
        for i in range(N):
            if board_temp[i][j] == "T":
                count += 1
        total_count += min(count, N-count)
    # 4. 현재 답보다 작다면 최소값이므로 저장
    answer = min(answer, total_count)

print(answer)