
Don't Go Show의 흔적들..
문제 접근
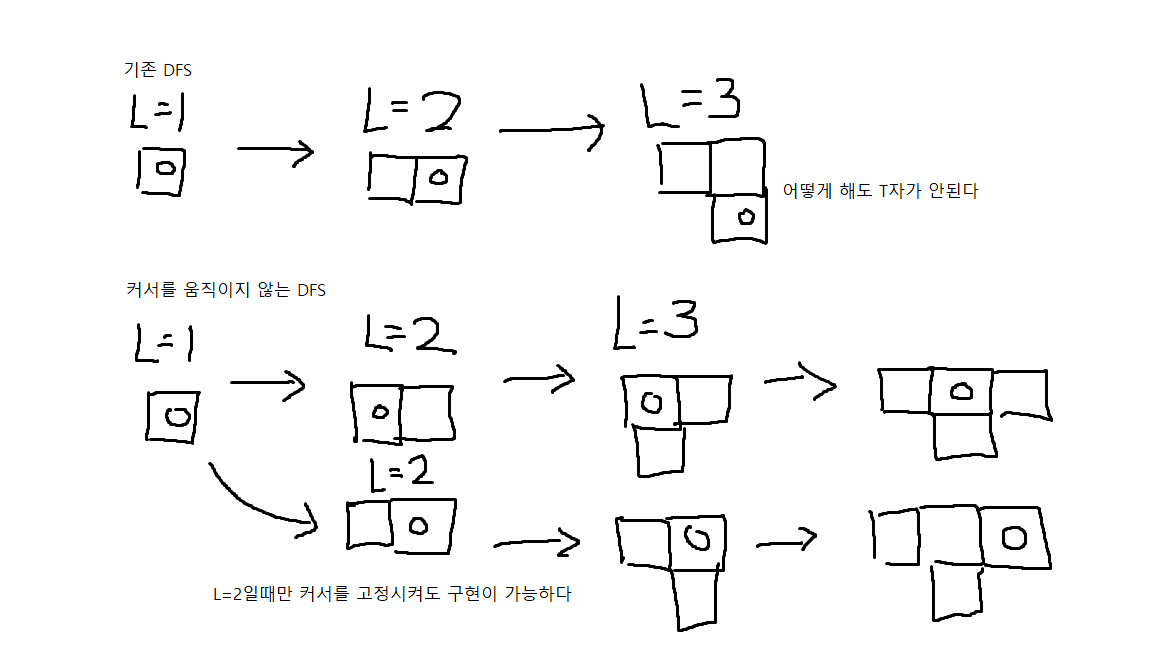
테트로미노 문제에서 가장 골치 아픈것은 바로 T자이다.
대부분의 도형은 DFS를 통해 구현이 가능하지만, T자만큼은 구현이 불가능하기 때문이다.
T자를 구현하기 위해서는 DFS를 돌 때, 현재 위치를 가리키는 커서를 움직이지 않도록 해야한다
풀이
시간 초과
import sys
input = sys.stdin.readline
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
answer = -1
def DFS(L, x, y, total):
global answer
if L == 4:
answer = max(answer, total)
else:
for k in range(4):
xx = x + dx[k]
yy = y + dy[k]
if 0<=xx<N and 0<=yy<M and ch[xx][yy] == 0:
ch[xx][yy] = 1
DFS(L+1, xx, yy, total+board[xx][yy])
DFS(L+1, x, y, total+board[xx][yy])
ch[xx][yy] = 0
if __name__=="__main__":
N, M = map(int,input().split())
board = [list(map(int,input().split())) for _ in range(N)]
ch = [[0]*M for _ in range(N)]
for i in range(0, N):
for j in range(0, M):
ch[i][j] = 1
DFS(1, i, j, board[i][j])
ch[i][j] = 0
print(answer)- 한번의 DFS를 돌 때 일반 DFS와 커서를 움직이지 않는 DFS를 모두 돌도록 했다.
- 가능한 모든 경우의 수를 탐색하는 방법이라, 안그래도 시간복잡도가 큰데 이걸 2번씩이나 하게 만들었으니... 시간초과가 뜰 수밖에 없었다.
7480ms
import sys
input = sys.stdin.readline
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
answer = -1
def solution(x, y):
def DFS(L, x, y, total):
global answer
if L == 4:
answer = max(answer, total)
else:
for k in range(1,4): # 변경점 2
xx = x + dx[k]
yy = y + dy[k]
if 0 <= xx < N and 0 <= yy < M and ch[xx][yy] == 0:
ch[xx][yy] = 1
DFS(L+1, xx, yy, total+board[xx][yy])
ch[xx][yy] = 0
def t_shape(L, x, y, total): # 변경점 1
global answer
if L == 4:
answer = max(answer, total)
else:
for k in range(4):
xx = x + dx[k]
yy = y + dy[k]
if 0 <= xx < N and 0 <= yy < M and ch[xx][yy] == 0:
ch[xx][yy] = 1
t_shape(L+1, x, y, total+board[xx][yy])
ch[xx][yy] = 0
def box_shape(x, y, total): # 변경점 2
global answer
xx = x + 1
yy = y + 1
if 0<=xx<N and 0<=yy<M:
answer = max(answer, total+board[xx][yy]+board[xx-1][yy]+board[xx][yy-1])
ch[x][y] = 1
DFS(1, x, y, board[x][y])
t_shape(1, x, y, board[x][y])
box_shape(x, y, board[x][y])
ch[x][y] = 0
if __name__ == "__main__":
N, M = map(int, input().split())
board = [list(map(int, input().split())) for _ in range(N)]
ch = [[0]*M for _ in range(N)]
for i in range(0, N):
for j in range(0, M):
solution(i, j)
print(answer)변경점 1
T자 도형을 탐색하는 함수를 따로 만들어서 board[i][j]마다 한번씩만 T자 도형의 최대값을 구하도록 했다.
T자 도형을 탐색하는 방법은 맨위 그림에서 커서를 고정한 상태로 주변을 탐색하는 방법을 사용했다.
변경점 2
그럼에도 불구하고 시간초과가 발생해서 이번에는 박스 모양의 도형도 별도의 함수로 뺐다.
박스 모양 도형을 빼면 DFS를 탐색할 때 4방향 모두를 탐색할 필요가 없기 때문이다.
박스 모양 도형의 최대값을 구하는 함수를 작성한 뒤, 기존 DFS에서 3방향만 탐색하도록 했다.
문제점
DFS에서 시간복잡도를 줄이는 가장 좋은 방법은 가지치기이다.
위 풀이는 이러한 점을 고려하지 못했다.
176ms
import sys
input = sys.stdin.readline
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
answer = -1
def DFS(L, x, y, total):
global answer
if L == 4:
answer = max(answer, total)
elif (total+max_value*(4-L)) <= answer: # 변경점2
return
else:
for k in range(4):
xx = x + dx[k]
yy = y + dy[k]
if 0 <= xx < N and 0 <= yy < M and ch[xx][yy] == 0:
ch[xx][yy] = 1
if L == 2: # 변경점 1
DFS(L+1, x, y, total+board[xx][yy])
DFS(L+1, xx, yy, total+board[xx][yy])
ch[xx][yy] = 0
if __name__ == "__main__":
N, M = map(int, input().split())
board = [list(map(int, input().split())) for _ in range(N)]
ch = [[0]*M for _ in range(N)]
max_value = max(map(max, board)) # 변경점2
for i in range(0, N):
for j in range(0, M):
ch[i][j] = 1
DFS(1, i, j, board[i][j])
ch[i][j] = 0
print(answer)변경점 1
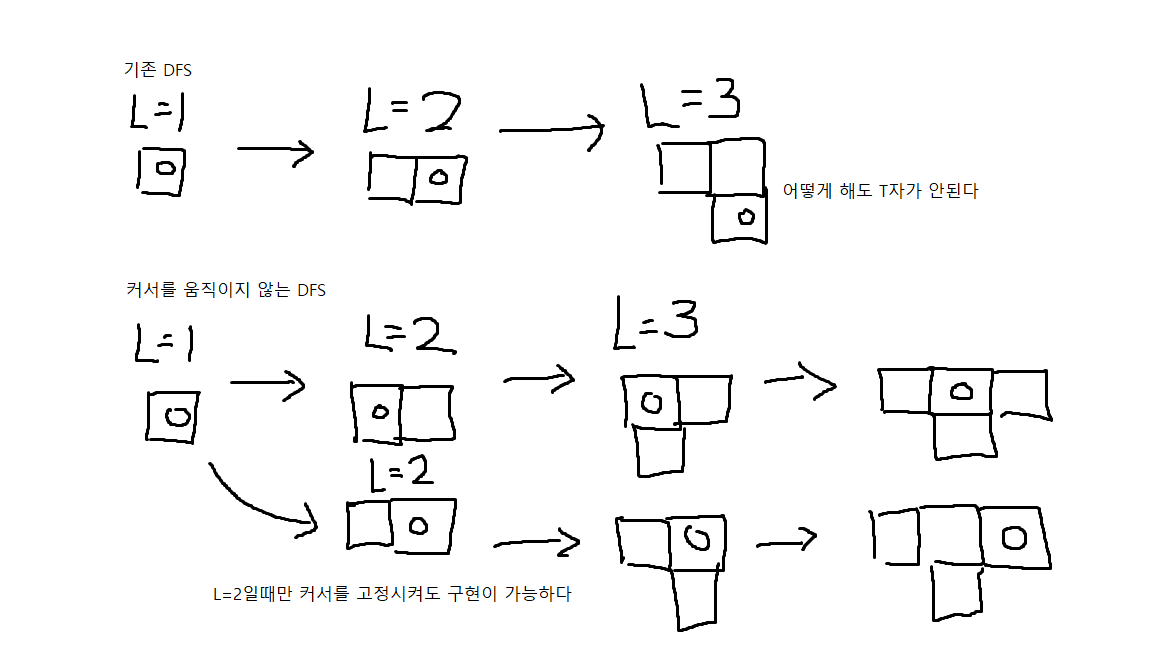
위 그림에서 L=2일 때, 한번만 커서를 고정시켜도 T자 도형을 탐색할 수 있다.
즉, 별도로 함수를 만들 필요 없이 조건문을 이용해서 L=2일 때만 커서를 움직이지 않는 DFS를 돌게한다면 T자 도형 탐색이 가능하다.
변경점 2 - 가지치기
가지치기는 DFS에서 시간 단축의 가장 중요한 요소이다
전체 배열에서 수의 최대값을 저장한 max_value 변수를 추가했다.
그리고 L번째 방문에서 남은 4-L 번의 방문을 모두 max_value로 한다고 해도 answer보다 크지 않다면 answer는 갱신되지 않을 것이고, 이는 더 이상 나머지 블록을 방문할 필요가 없다는 뜻이다.
if (total+max_value*(4-L)) <= answer: 이 조건문을 통해 더 이상 방문을 해도 최대값을 갱신할 가망이 없을 때 그대로 return 해버리는 가지치기를 추가했다.
배운점
- DFS 탐색 시 조건문을 통해 다양한 변형 및 응용이 가능하다.
- DFS로 최대값을 구할 때, max_value를 이용해 가지치기가 가능하다.

