문제 : https://www.acmicpc.net/problem/2110

문제 요약

1차원 공간에 N개의 집이 위치해 있을 때 C개의 공유기를 설치해서 공유기 사이의 거리가 최대가 되도록 하는 문제이다.

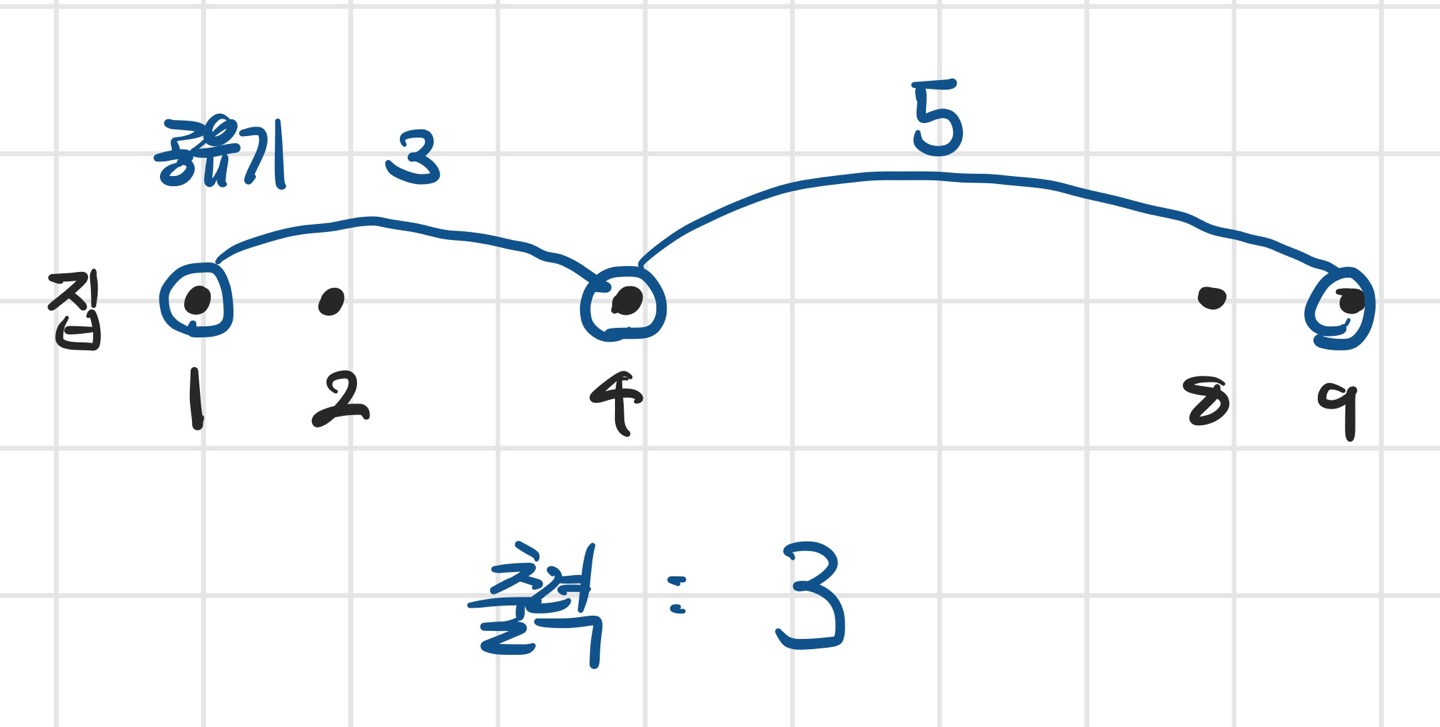
위와 같이 1, 2, 4, 8, 9 좌표에 3개의 공유기를 설치해야 한다면
1, 4, 8 또는 1, 4, 9에 설치하는 것이 공유기 사이 거리를 최대로 할 수 있고, 출력은 3이 된다.

풀이 - 이분탐색

풀이 방법은 거리에 대한 이분탐색을 이용해서 풀 수 있다.

위에서 봤던 5개의 집 중 3개를 설치하는 예제를 통해 알아보자

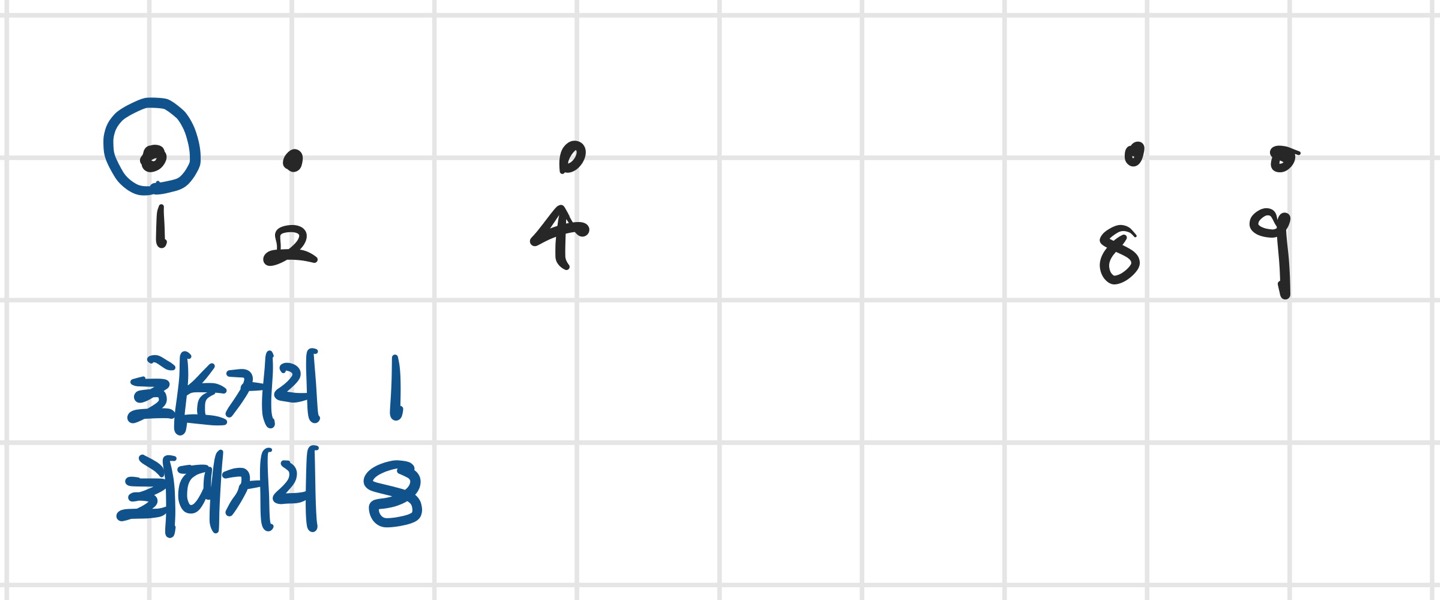
먼저 가장 왼쪽 끝 집에 무조건 공유기 하나를 설치한다고 가정한다. (오른쪽 끝집이어도 상관 X)
현재 공유기를 설치할 수 있는 최소 거리는 1, 최대 거리는 8이다.
이분 탐색을 위해 (1 + 8) // 2 = 4를 탐색거리로 설정한다.

이제 공유기 간의 거리가 최소 4가 되도록 했을 때 몇 개를 설치할 수 있는지 구한다.

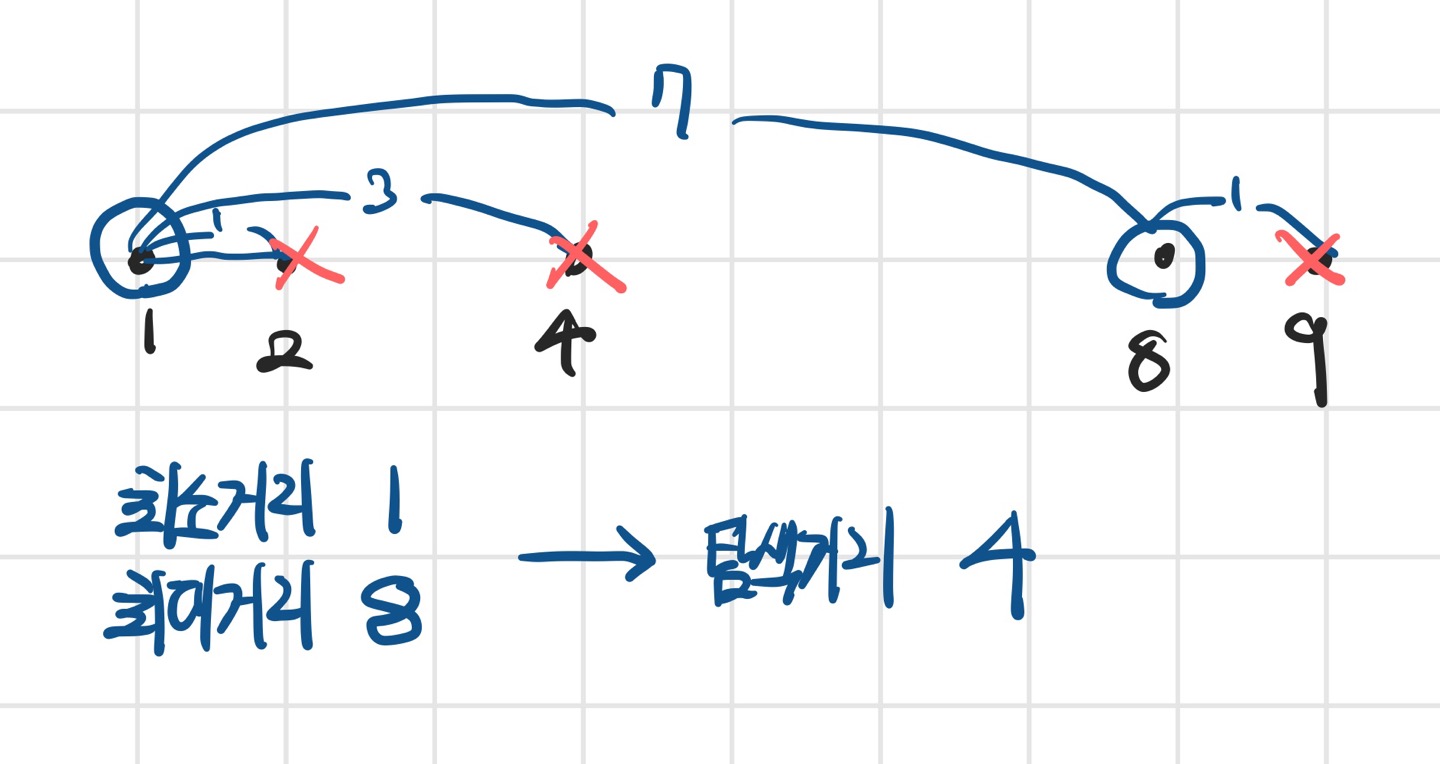
위와 같이 구해보면 1, 8에 2개의 공유기를 설치할 수 있다.
우리가 설치하고자 하는 공유기 3개에 못 미치므로 최대거리는 적어도 4보다 작다는 것을 알 수 있다. 즉, 탐색 범위를 [1, 3]으로 좁히면 된다.

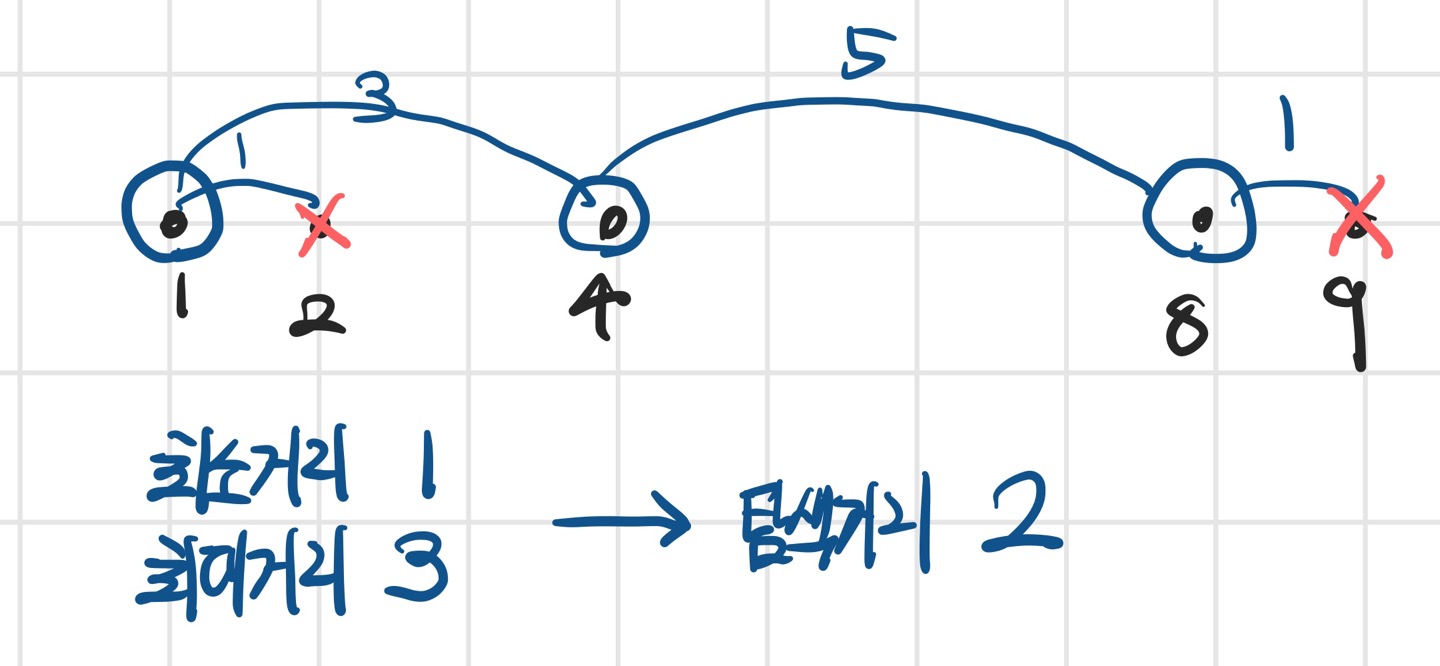
공유기 간의 거리가 최소 2가 되도록 했을 때 3개의 공유기를 설치할 수 있다.
우리는 3개를 설치하면서 공유기 간의 거리가 최대인 거리를 알고 싶으므로, 최소거리를 늘려서 탐색을 계속하면 된다.

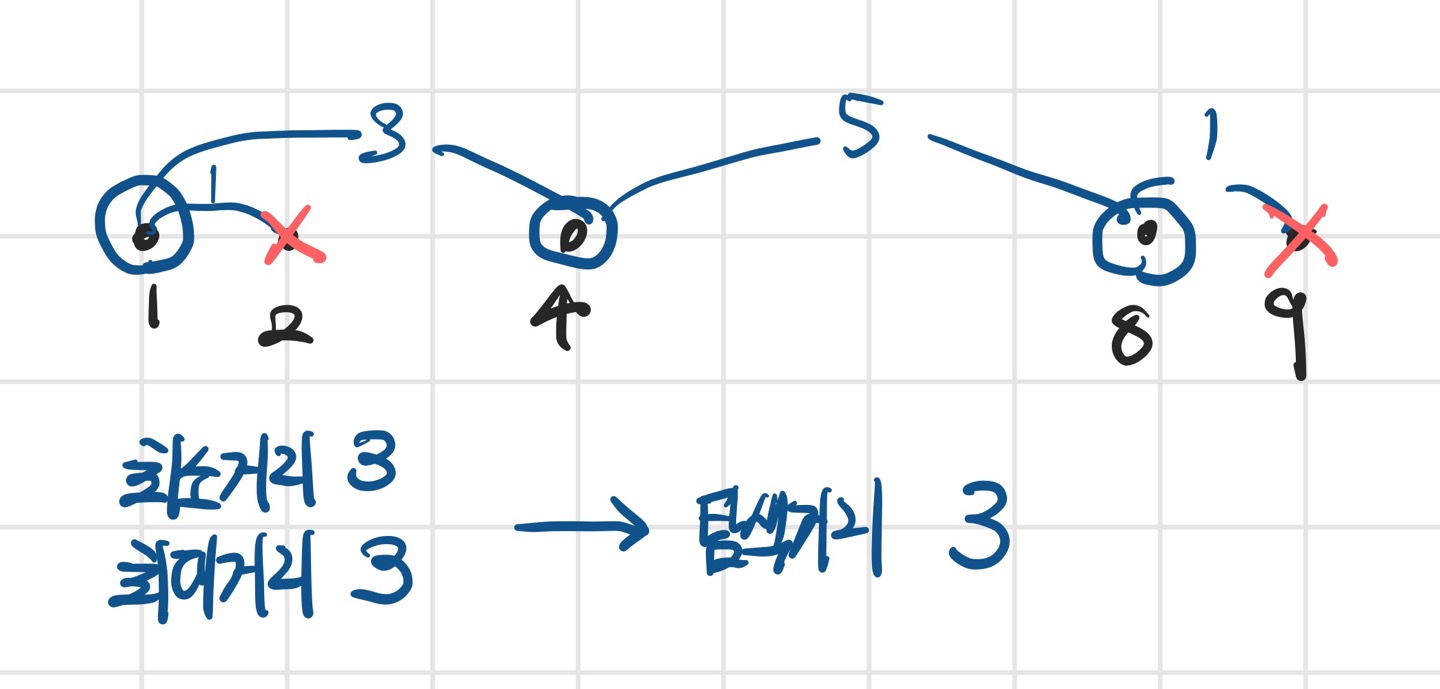
탐색거리 3에서도 1, 4, 8에 3개의 공유기를 설치할 수 있다.
이때 최소거리와 최대거리의 역전이 일어나므로 더 이상 탐색하지 않고 현재 최대 거리인 3을 출력 후 탐색을 종료하면 된다.

주의 사항

• 탐색 거리를 잘 정해주어야 한다.
  N이 최대 20만인데 최소 거리를 일일히 구해주는 것은 비효율적이므로 그냥 1로 잡고
  최대 거리는 왼쪽 끝집과 오른쪽 끝집 사이의 거리가 된다. (house[-1] - house[0])

• 탐색 경계값을 잘 정해주어야 한다.
  이건 이분 탐색에서 공통적으로 주의해야 할 부분이다. 자칫하면 무한루프에 빠지거나 탐색 값을 건너뛰게 될 위험이 있기 때문이다.
  이번 풀이의 경우 최소거리(left)와 최대거리(right)가 역전될 때 탐색을 종료하도록 하면서, 탐색 범위를 갱신할 때 탐색거리(mid)+1 또는 mid-1이 되도록 하여 무한루프에 빠지지 않도록 했다.

코드

import sys

input = sys.stdin.readline

# 설치 간격이 distance일 때 설치할 수 있는 공유기의 수를 구하는 함수
def install(distance):
    count = 1 # 제일 왼쪽에 하나 설치되었다고 가정
    left, right = 0, 1
    while right < N:
        # 두 포인터가 가리키는 집 사이 거리가 distance보다 크거나 같으면 설치
        if distance <= hubs[right] - hubs[left]:
            count += 1
            left, right = right, right+1
        # 설치 거리가 안되면 right 포인터 전진
        else:
            right += 1

    return count


# 이분 탐색을 통해 C개 설치가 가능한 최대 거리 탐색
def binary_search(left, right):
    answer = 1
    while left <= right:
        mid = (left + right) // 2
        count = install(mid)
        
        # count가 C보다 작으면 왼쪽 탐색
        if count < C:
            right = mid - 1
        # count가 C보다 크거나 같으면 오른쪽 탐색하고 반환할 값 갱신
        else:
            left = mid + 1
            answer = mid

    # upper bound이므로 right값 반환
    return answer
    

if __name__ == "__main__":
    # 입력 받기
    N, C = map(int, input().split())
    hubs = [int(input()) for _ in range(N)]
    
    # 순차 탐색을 위해 배열 정렬
    hubs.sort()
    
    print(binary_search(1, hubs[-1] - hubs[0]))

코멘트

사실 이분 탐색 문제가 거기서 거기라고 생각해서
code plus 문제집을 풀 때 그냥 건너 뛰었는데

이번 문제에서 해결책을 못찾아서 (거리를 기준으로 이분 탐색하는 걸 상상도 못함) 오랫동안 해메었다.

역시 공부해야 하는 알고리즘은 다 이유가 있는 것 같다.
앞으로는 빼먹지 말고 모든 알고리즘을 성실히 공부해야지

일단 이분탐색 문제를 위주로 더 많이 풀어봐야 할 것 같다.