비트마스크란?

비트마스크(BitMask)는 데이터를 저장하는 하나의 방법이다.

일반적으로 파이썬에서는 데이터를 리스트에 저장한다.
0, 1 또는 True, False 등의 두 종류의 값이 저장되는 리스트가 있다고 생각해보자.

A = [0, 1, 1, 1, 1, 0, 1, 0]
A_bool = [False, True, True, True, True, False, True, False]

컴퓨터는 모든 자료를 0과 1의 이진수로 저장한다.
예를들어 Java 기준 int 자료형은 4Byte(32bits) 다음과 같이 저장된다.

4 = 00000000 00000000 00000000 00000100
9 = 00000000 00000000 00000000 00001001
122 = 00000000 00000000 00000000 01111010
-1 = 11111111 11111111 11111111 11111111

맨 앞의 비트 1개는 부호를 나타내며, 실제로 int 자료형이 저장할 수 있는 최대값은 2^31-1, 즉 2,147,---,--- 이다.

위 수에서 122의 이진수를 보면 배열로 예시를 들었던 리스트와 형태가 일치하는 것을 볼 수 있다.
정수 122는 리스트 A의 데이터를 저장하는 또 하나의 방법이 될 수 있다는 것이다.

마찬가지로 int 자료형의 모든 정수는 32개의 이진 데이터를 저장할 수 있다.
이렇게 하나의 비트를 데이터 저장소로 활용하는 방법을 비트마스크라고 한다.

비트마스크의 장점

1. 메모리를 적게 사용한다.
32개의 데이터를 저장하는 리스트를 만든다면 약 4 * 32Byte의 공간이 필요하다.
하지만 비트마스크를 이용하면 4Byte 정수 한개로 데이터를 저장할 수 있다.
저장해야할 데이터가 많을 수록 비트마스크를 이용하면 메모리 절약에 매우 유용하다.

2. 연산이 빠르다.
비트마스크에는 '비트연산자'를 사용하는데, 대부분 O(1)의 공간복잡도를 갖는다.
다른 자료구조를 이용하는 것보다 빠르게 연산을 처리할 수 있다.

비트 연산자

비트마스크를 수행하기 위해 알아야 할 연산자들이다.

1. | : OR
   두 비트 중 어느 한쪽이라도 1이면 1이다.
   1 | 1 = 1
1 | 0 = 1
0 | 0 = 0

2. & : AND
   두 비트가 모두 1이어야 1이다.
   1 & 1 = 1
1 & 0 = 0
0 & 0 = 0

3. ~ : NOT
   1이면 0, 0이면 1이다.
   ~1 = 0
~0 = 1

4. ^ : XOR
   두 비트가 같은 값일 경우 0, 서로 다른 값일 경우 1이다.
   1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 0 = 0

5. << : Left Shift
   비트를 왼쪽으로 밀어낸다. 밀어낸어 생긴 마지막 비트의 빈칸은 0이 된다.
   1010 << 1 = 0100
1010 << 2 = 1000
1010 << 3 = 0000

6. >> : Arithmetic Right Shift
   부호를 유지한 채로 비트를 오른쪽으로 밀어낸다.
   즉 첫 비트는 shift하지 않고, 두번째 비트부터 오른쪽으로 밀린다.
   두번째 비트에 생긴 빈칸은 0으로 채운다.
   ※ 편의상 8bit만 고려
   00000100 >> 1 = 00000010 (4 >> 1 = 2)
   11111111 >> 2 = 10011111 (-1 >> 2 = -31)

7. >>> : Logical Right Shift
   무조건 비트를 오른쪽으로 밀어낸다.
   첫번째 비트에 생긴 빈칸은 0으로 채운다.
   11111111 >>> 2 = 00111111 (-1 >>> 2 = 63)

파이썬의 비트연산자 우선순위

파이썬의 연산 우선순위를 자세히 다루진 않겠지만

비트 연산자 기준으로
NOT > Shift > AND, OR, XOR
이 정도만 알아두면 될 것 같다.

비트마스킹 실습

백준 비트마스킹 문제 : 11723. 집합

위 백준 문제를 통해 비트마스킹을 실습해볼 수 있다.

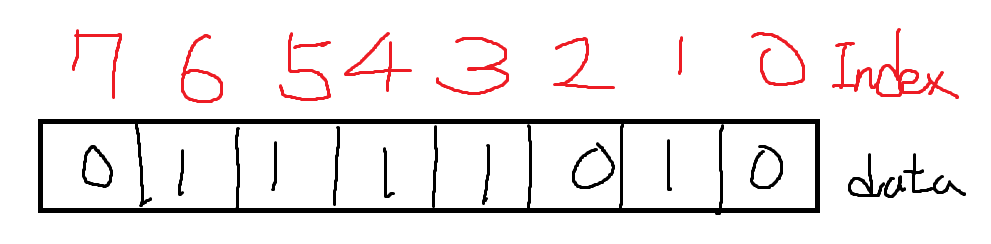
이진수를 자료구조로 생각하면 오른쪽부터 채워지므로, 인덱스를 거꾸로 생각해야한다는 점에 유의하자.

add

원하는 인덱스에 1을 추가하는 연산

122 = 00000000 00000000 00000000 01111010

여기서 n=2 인덱스에 1을 집어넣고 싶을 때 어떻게 하면 될까?

1. num=1 인 정수 변수를 만들고 n=2만큼 left shift를 한다.

   • 00000001 << 2 = 00000100

2. shift 된 값과 정수 122를 | (or) 연산한다.

   • 01111010 | 00000100 = 01111110

data = 122
num = 1
n = 2

print(bin(data))
# >>> 0b1111010
print(bin(data | (num << n)))
# >>> 0b1111110

※ bin()은 숫자를 이진수로 나타내는 함수이며, 0b는 이진수임을 표시한다.
※ print된 이진수 값에서 앞의 0은 모두 생략된다.

이렇게 n만큼 left shift된 정수를 생성해 or 연산 하는 것으로 원하는 인덱스에 1을 추가할 수 있다.

remove

원하는 인덱스를 0으로 바꾸는 연산

add와 반대로 n 인덱스의 값을 0으로 바꾸고 싶다면?
NOT 연산과 AND 연산을 이용할 수 있다.

n=3인덱스의 값을 0으로 바꾸고 싶은 경우

1. num << n 연산을 통해 n번 인덱스 값만 1인 비트를 생성
   • 00000001 << 3 = 00001000
2. not 연산하면 n번 인덱스 값만 0, 나머지가 모두 1인 비트가 된다.
   • ~00001000 = 11110111
3. 이를 데이터와 and 연산하면 n번 인덱스는 무조건 0이 되며, 나머지는 자기 자신 값이 나오게 된다.

data = 122
num = 1
n = 3

print(bin(data))
# >>> 0b1111010
print(bin(data & ~(num << n)))
# >>> 0b1110010

check

원하는 인덱스의 값을 확인하는 연산

AND 연산을 이용할 수 있다.

n=4 인덱스의 값을 확인하고 싶은 경우

1. num << n 연산을 통해 n번 인덱스 값만 1인 비트를 생성
   • 00000001 << 4 = 00010000
2. 그대로 데이터와 and 연산하면, n번 인덱스만 자기 자신이고, 나머지는 모두 0인 비트를 얻는다.
   • 01111010 & 00010000 = 00010000
3. 조건문에서 0이면 False, 0이 아닌 수는 모두 True임으로 조건문을 통해 True면 n번 인덱스의 값은 1, False면 n번 인덱스의 값은 0임을 알 수 있다.

data = 122
num = 1
n = 4

print(bin(data))
# >>> 0b1111010
if data & num << n:
    print(True)
else:
    print(False)
# >>> True

Toggle

원하는 인덱스의 값을 토글하는 연산 (1이면 0, 0이면 1로 변환)

XOR 연산을 이용할 수 있다.
0과 XOR연산을 할 경우 자기 자신이 출력된다.
1과 XOR연산을 할 경우 자신이 1이면 0, 0이면 1이 출력된다.

n=1 인덱스의 값을 toggle하고 싶은 경우

data = 122
num = 1
n = 1

print(bin(data))
# >>> 0b1111010
print(bin(data ^ num << n))
# >>> 0b1111000

all & empty

all은 모든 비트값을 1로 바꾸고, empty는 모든 비트값을 0으로 바꾼다.
이는 쉽게 할 수 있다.

data를 -1로 초기화 하면 모든 비트값이 1이 된다.
data를 0으로 초기화 하면 모든 비트값이 0이 된다.