안녕하세요!
딥러닝 기초 지식을 한번에 정리하고 싶은 분들을 위해 딥러닝 기초 개념을 담아보았습니다. 깊고 자세한 이론은 소개하지 않지만 필수 지식의 핵심은 빠르게 짚고 넘어가고자 합니다.
1. 퍼셉트론(Perceptron)이란?
퍼셉트론은 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 제안한 초기 형태의 인공 신경망 알고리즘입니다. 우리 뇌의 뉴런의 동작과 비슷하며 다수의 입력으로부터 하나의 값을 출력합니다.
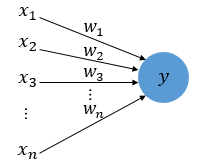
구성요소
x는 입력값, w는 가중치, y는 출력값을 뜻합니다.
(그림의 원은 노드 혹은 뉴런이라고 부릅니다. )
출력 원리
입력값이 각 고유 가중치와 곱해져 다음 노드로 보내지며, 이때 각 입력값과 가중치의 곱의 전체의 총합이 임계값를 넘어야 1이 출력됩니다. 그렇지 않을 경우에는 0이 출력됩니다. 즉, 가중치가 클수록 해당 입력값이 중요함을 알 수 있습니다.
수식
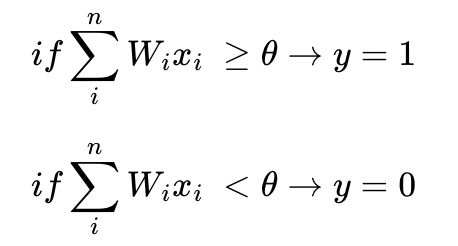
위의 출력 원리를 수식으로 나타내면 위와 같으며 계단 함수라고 합니다.
단, 임계값을 좌변으로 넘기고 편향으로도 표현할 수도 있습니다.
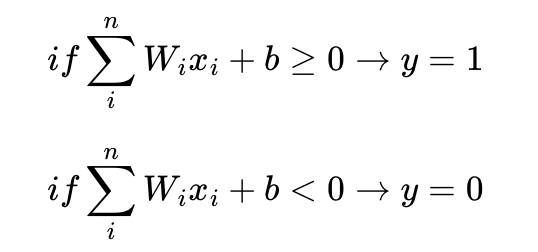
편향(bias)를 추가한 수식은 위와 같습니다.
편의상 편향을 수식에서 생략하기도 하지만 실제로는 딥러닝에서 최적값을 찾아야 할 변수 중 하나입니다.
이렇게 노드에서 출력값을 변경시키는 함수를 활성화 함수(Activation Function)라고 합니다. 퍼셉트론은 활성화 함수로 "계단 함수"를 사용하였지만, 이외에도 여러 다양한 활성화 함수가 있습니다. 활성화 함수는 추후 소개하도록 하겠습니다.
학습 방법
임의로 설정된 가중치(weight)에서 시작하며 원하는 출력값이 나오지 않으면 가중치를 개선해나가는데 이를 학습이라고 합니다.
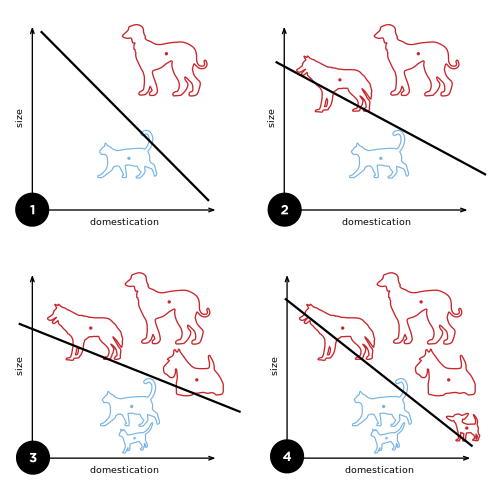
위의 그림을 보면 학습이 반복될수록 기울기가 달라지는 것이 보이시나요?
가중치가 조정되어 강아지와 고양이를 분리하는 것을 볼 수 있습니다.
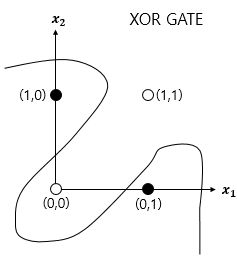
하지만 퍼셉트론의 한계가 나타납니다. 직선 하나로 나눈 영역만 분리할 수 있어 XOR과 같은 곡선 형태(비선형 영역)는 분류가 불가능하다는 단점이 있습니다.
이 문제는 어떻게 해결할까요?
2. 다층 퍼셉트론(MultiLayer Perceptron, MLP)
AND, NAND, OR 게이트를 조합하여 XOR 게이트를 구현할 수 있는 것처럼 한 층을 더 쌓아 단층 퍼셉트론에서 다층 퍼셉트론을 만들 수 있습니다.
입력층과 출력층만 존재하는 단층 퍼셉트론과 달리, 입력층과 출력층 사이에 존재하는 층을 은닉층(hidden layer)이라고 합니다.
즉, 은닉층이 존재한다는 점이 단층 퍼셉트론과 차이점이며 다층 퍼셉트론은 줄여서 MLP라고도 부릅니다.
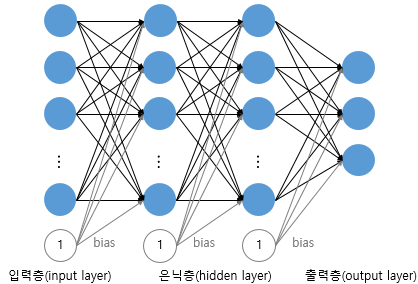
위의 그림처럼 은닉층이 2개 이상이면 심층 신경망(Deep Neural Network, DNN)이라고 합니다. 다층 퍼셉트론만 뿐만 아니라 변형된 다양한 신경망들도 은닉층이 2개 이상이 되면 심층 신경망이라고 합니다.
앞서 언급한 것처럼 가중치를 개선해나가는 것을, 기계가 가중치를 스스로 찾아내도록 자동화하는 것을 머신 러닝에서 말하는 학습이라고 하며 이때 손실 함수(Loss function)와 옵티마이저(Optimizer) 등을 사용합니다.
3. 활성화 함수(Activation Function)
퍼셉트론에서 언급했던 활성화 함수는 입력값의 총합을 출력값으로 변환하는 함수입니다. 인공 신경망에서 활성화 함수는 입력값을 출력을 결정하는 함수로 매우 중요하며 은닉층에서 층(layer)을 깊게 쌓아도 값을 가져갈 수 있어야 하므로 주로 비선형 함수를 사용하는게 일반적입니다. 주로 사용하는 활성화 함수를 간략히 설명합니다.
대표적인 활성화 함수
1. 시그모이드 함수(Sigmoid function)
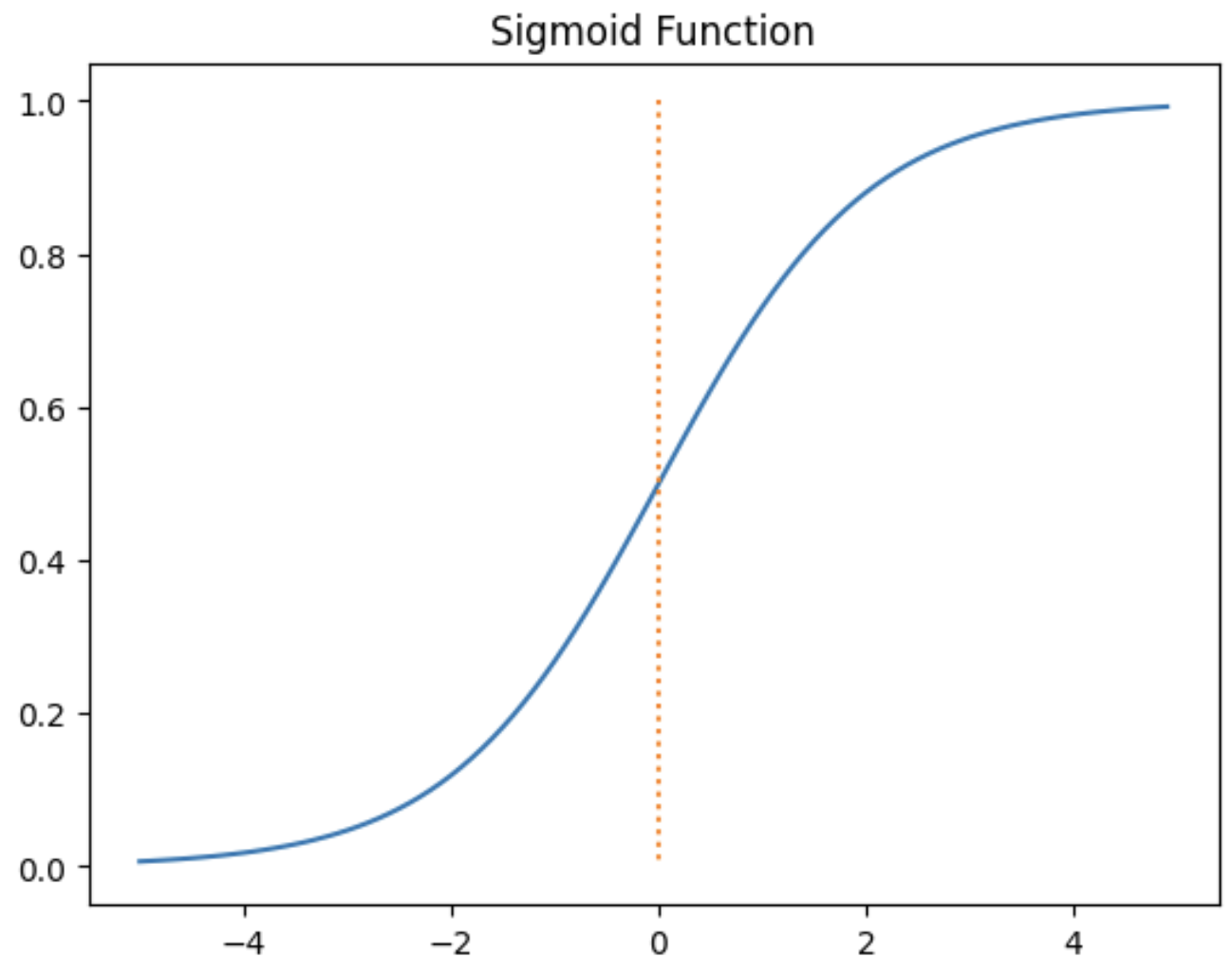
특징
- 시그모이드 함수는 Logistic function으로 불립니다.
- 출력값은 0과 1 사이
- 입력값이 매우 큰 값이면 출력값은 거의 1이며, 매우 작은 값이면 0에 가깝습니다.
- 입력값이 크거나 작아질수록 기울기가 0에 가까워집니다.
- 이진 분류에서 사용됩니다.
단점
- 입력값이 커/작아짐에 따라 기울기가 0에 가까워지는 기울기 소실이 존재
- 함수값 중심이 0이 아니기 때문에 학습이 느려질 수 있습니다.
- exp 함수 사용 시 연산 비용이 큽니다.
2.소프트맥스 함수(Softamx function)
특징
- 시그모이드 함수를 일반화한 함수
- 세 가지 이상의 다중 클래스 분류(MultiClass Classification)에서 주로 사용됩니다.
3. tanh 함수, (Hyperbolic tangent function)
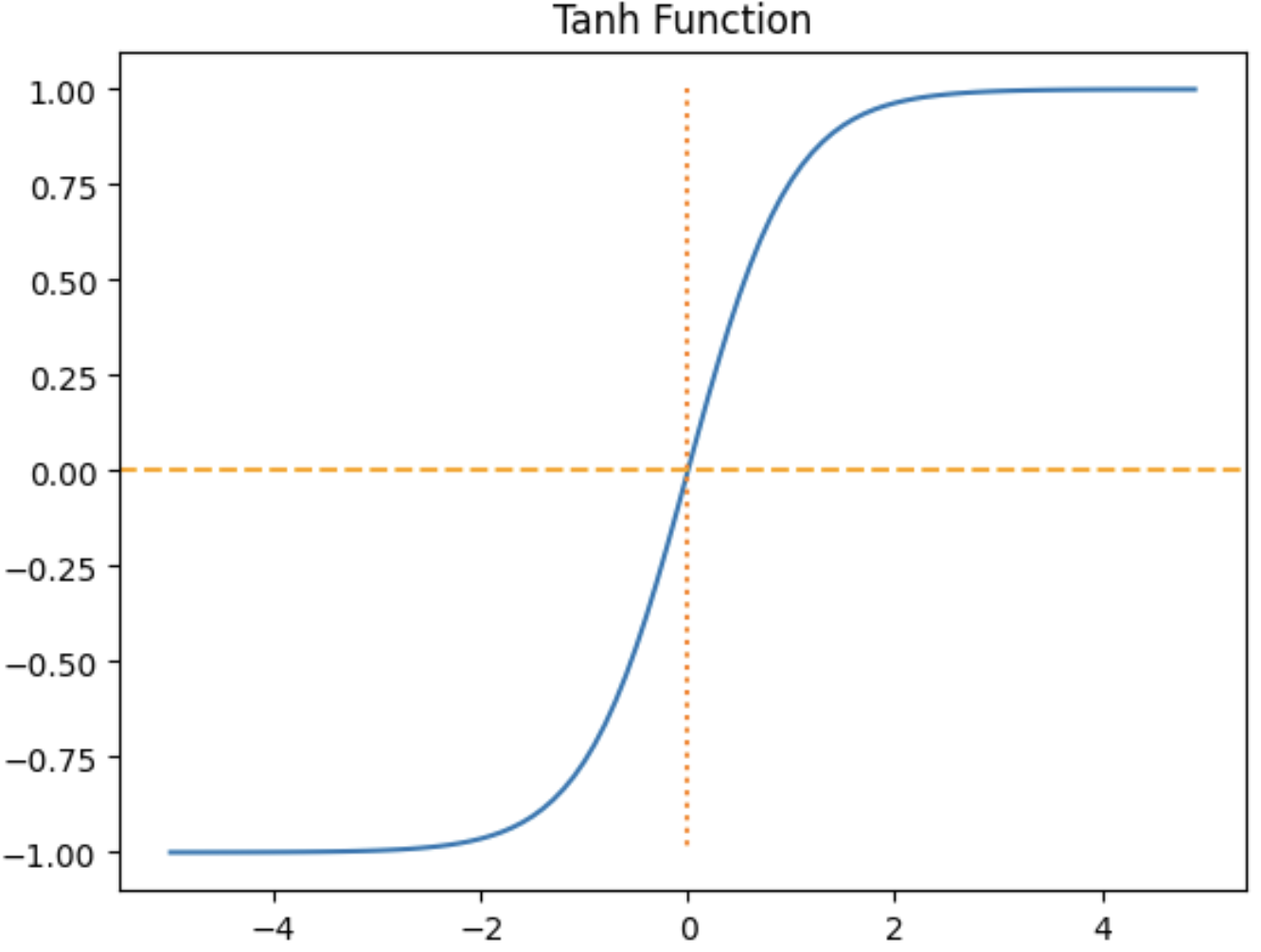
특징
- 함수의 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결합니다.
- 출력값이 -1과 1 사이입니다.
- 입력값이 작으면 출력값은 0에 가까워지고, 입력값이 커질수록 1에 가까워집니다.
단점
- 여전한 기울기 소실 문제가 존재합니다.
4. ReLU
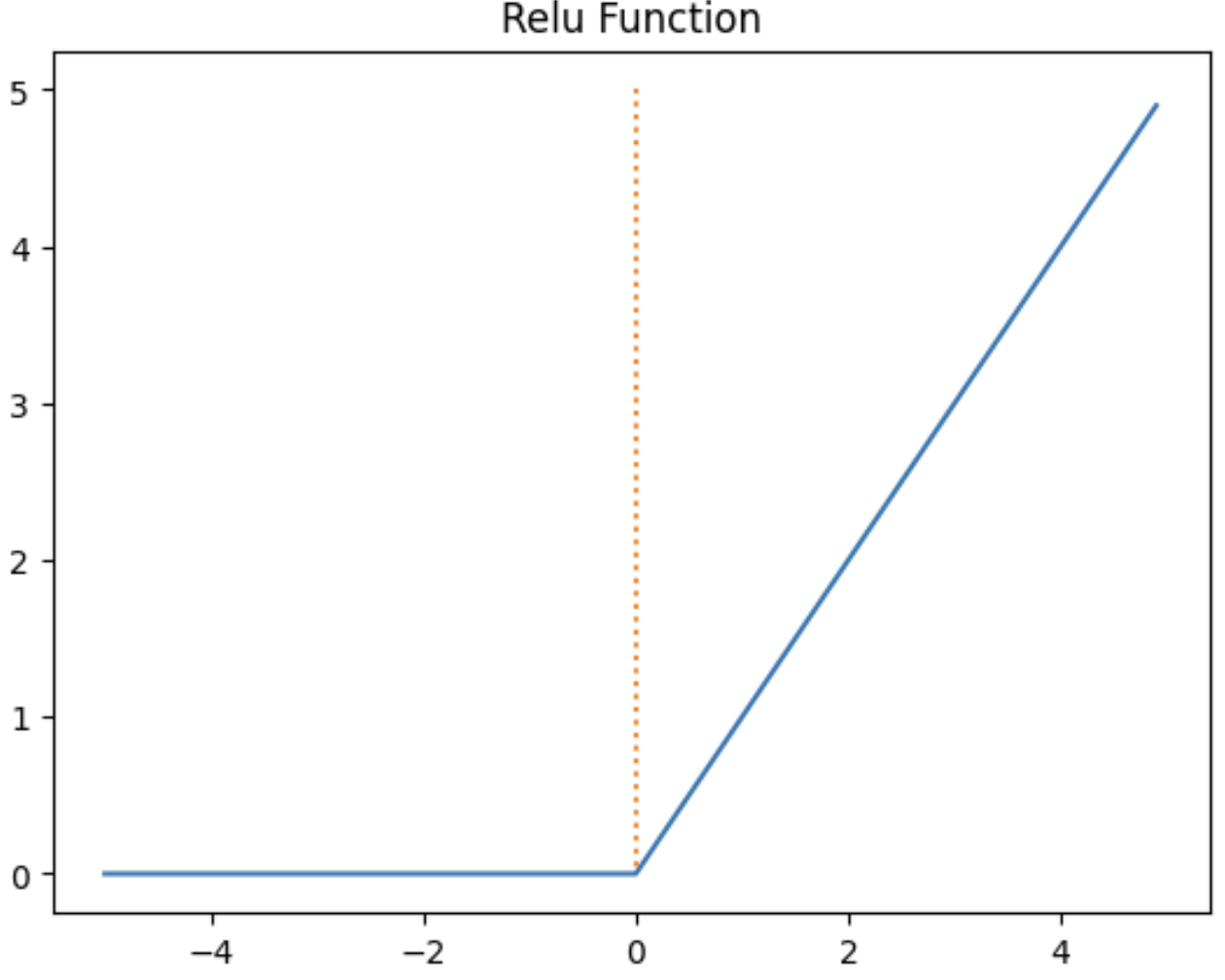
특징
- x > 0 이면 기울기가 1인 직선이고, x < 0이면 함수값이 0이된다
- 시그모이드, tanh 함수보다 학습이 속도가 빠릅니다
- 연산 비용이 적습니다.
단점
- x < 0인 값은 기울기가 0이기 때문에 뉴런이 죽을 수 있는 Dying ReLU 문제가 존재합니다.
5. Leaky ReLU
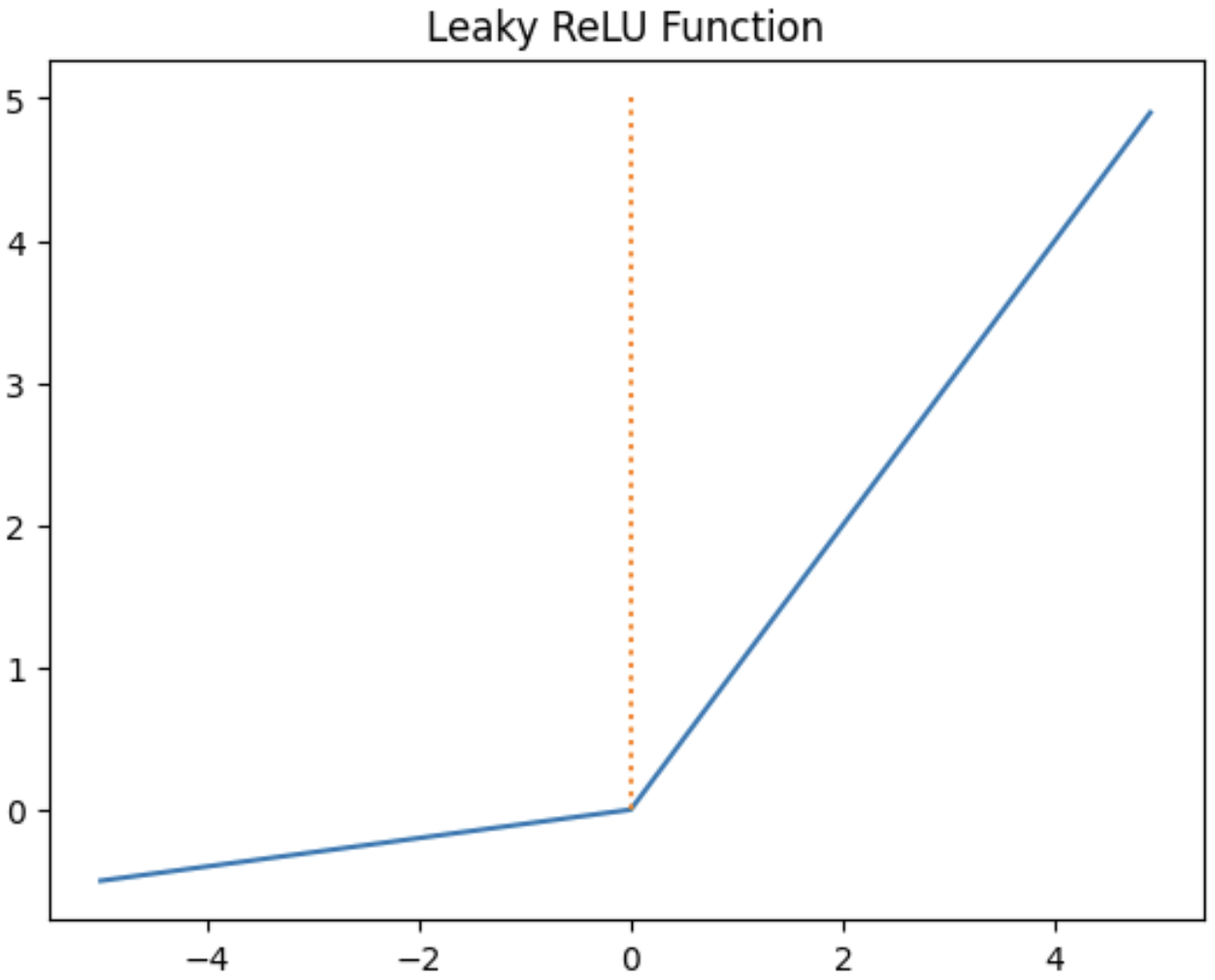
특징
- Dying ReLU 문제를 보완하기 위한 ReLU의 변형 함수입니다.
- x < 0 경우 0이 아니라 0.001과 같은 매우 작은 수를 반환합니다.
마무리
이번 포스팅에서는 퍼셉트론과 활성화 함수에 대해 알아보았습니다.
다음 포스팅은 CNN (이론)에 대해 설명드리겠습니다. 또한 추후 컴퓨터 비전 분야로 영역을 넓혀 포스팅을 할 예정이니 많은 관심 부탁드립니다!
참고 출처
https://wikidocs.net/60680
https://en.wikipedia.org/wiki/Perceptron
https://keras.io/api/layers/activations/#softmax-function
https://reniew.github.io/12/