저번시간에 CFG(Context Free Grammar)에 대해 이야기하다 끝을 냈다.
예시
- L(G)={a2nbn∣n≥0}
- CFG G = {{S},{a,b},S,P}
- P : S →aaSb ∣ ϵ
- L(G)={ambn∣n≤m≤2n}
- CFG G = {{S},{a,b},S,P}
- P : S →aSb ∣ aaSb ∣ ϵ
- L(G)={am+nbmcn∣m≥0,n≥1}
- CFG G = {{S,A},{a,b,c},S,P}
- P : S →aSc ∣ aAc
- A →aAb ∣ ϵ
위의 예시처럼 CFL을 보고 CFG의 production rule을 만들 수 있다. 익숙하지 않다면 어렵지만 어느정도 연습을 하다보면 위의 예시처럼 간단한 언어는 나타낼 수 있다.
다음은 펠린드롬 예시와 함께 다른 예시도 살펴보자.
- L(G)={w∈{a,b}∗ ∣ w=wR, ∣wwR∣ is even}
- CFG G = {{S},{a,b},S,P}
- P : S →aSa ∣ bSb ∣ ϵ
- L(G)={w∈{a,b}∗ ∣ w=wR, ∣wwR∣ is odd}
- CFG G = {{S},{a,b},S,P}
- P : S →aSa ∣ bSb ∣ a ∣ b
- L(G)={ambncndm∣m,n≥1}
- CFG G = {{S,A},{a,b,c,d},S,P}
- P : S →aSd ∣ aAd
- A →bAc ∣ bc
4번째 예시는 펠린드롬이면서 스트링의 길이가 짝수인 경우이고 5번째 예시는 스트링의 길이가 홀수인 경우이다. 전체적인 구조는 비슷하고 엡실론 혹은 알파벳으로 터미널을 구성한다는 점에서 차이가 있다.
CFG는 유일할까?
답은 유일하지 않다. 언어가 주어졌을 때 나타낼 수 있는 CFG는 다양하다.
어디에 쓰일까?
괄호 짝 맞추기를 나타낼 수 있다.
G=({S},{(,)},S,P)
P : S→(S) ∣ SS ∣ ϵ
if, else 구문을 구분하는 용도로 사용할 수 있다.
G=({S},{i,e},S,P)
P : S→iS ∣ iSeS ∣ SS ∣ ϵ
Derivation 과정
예를 들어
G=({S},{0,1},S,P)
P : S→0S1 ∣ 1S0 ∣ SS ∣ ϵ
w = 011100 ∈ L(G) 일까?
- S→SS→0S1S→01S→0S11S0→0S111S00→011100
- S→SS→S1S0→S11S00→S1100→0S11100→011100
다음 두 과정을 보자.
1번은 왼쪽 변수를 먼저 derivation했고 2번은 오른쪽 변수를 먼저 derivation했다. 이처럼 CFG의 derivation은 크게 2가지로 나뉜다.
- Leftmost Derivation
- Rightmost Derivation
좌우선 변환, 우우선 변환이라고 번역할 수 있다.
Parse trees
위 과정을 쉽게 도와줄 수 있는 표현 방식인 parse tree이다.
- 루트는 start symbol이다.
- leaf node는 ϵ 혹은 터미널 변수이다.
- 그밖의 internal node는 변수다.
- parse tree의 yield는 왼쪽부터 오른쪽 순서대로 leaf node를 의미한다.
- 터미널 심볼로만 이루어져 있다.
- yield의 모음이 바로 그 문법의 언어이다.
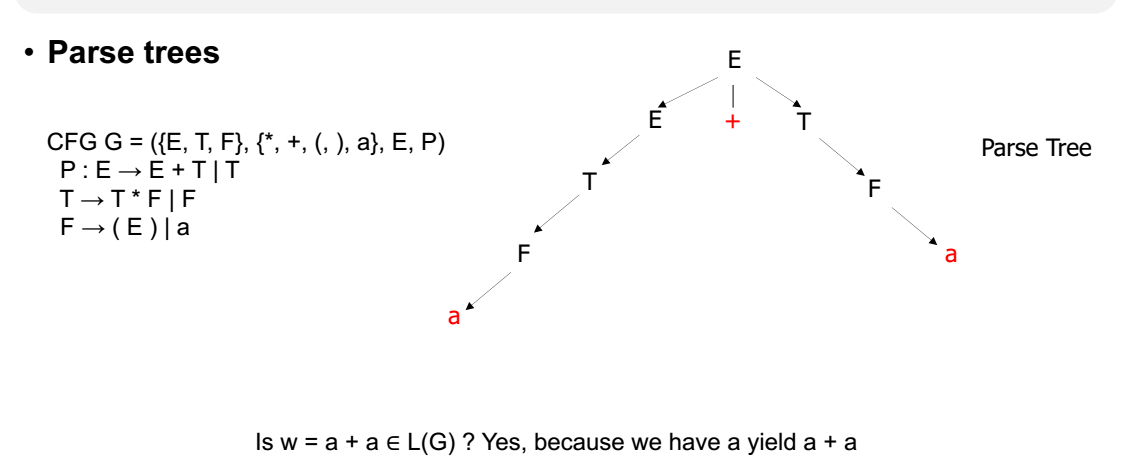
그럼 parse tree는 unique할까?
아니다.
이상적으로는 parse tree가 하나만 존재하여 string w에 대한 syntatic structure를 파악하면 좋겠지만 CFG는 ambiguity한 특성을 지닌다.
예를 들어 dangling else를 생각해보자.
if(expr) {
if (expr) {
} else {
}
}
위 구조와
if(expr){
if(expr){
}
} else{
}
이 구조는 yield로 표현하면 iiaea로 같은 표현식이 된다. i와 e가 if, else이다. parse tree로 나타내면 다음과 같다.
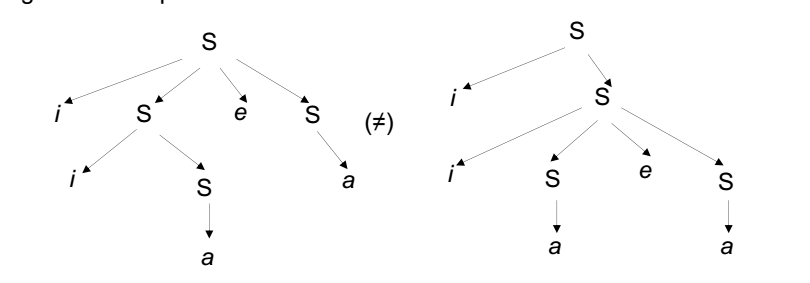
이처럼 parse tree를 하나로 나타낼 수 없으며 문법만 봤을 때는 어느 구조가 맞는지 판단하기 어렵다.
만약 산술 연산자가 들어간 문법에 대해서는 우선순위 개념을 도입하면 쉽게 해결된다. 하지만 dangling else와 같은 문제는 어떻게 해결할 수 있을까?


