AES에 대해 설명하기 전에 갈로아 필드, 특히 $GF(2^8)$에 대해 알고 있어야한다.

AES

AES는 DES에서 연장된 버전으로 차이점은 블록 사이즈와 블록 암호화와 복호화에 사용하는 키 사이즈가 128bits로 늘어난 것이다. 즉, 기저에는 Block cipher가 깔려있다.

종류

크게 3가지로 키의 길이에 따라 그리고 암호화 알고리즘 속 라운드 수에 따라 구분한다.

• AES-128
• AES-192
• AES-256

아니 키 사이즈는 128로 고정이라고 하지 않았냐?

여기서 128로 고정한 것은 각 블록 암호화 또는 복호화에 사용될 키의 길이로 기존의 키를 변형한 값이다. 즉 128bits짜리 키를 쓰든 192bits, 256bits짜리를 쓰든 각 블록과 함께 사용할 키는 128bits로 바꿀 것이다.

state

Block cipher의 개념대로 모든 평문을 한번에 암호화하는 것이 아니라 block 단위로 암호화를 하고 암호화한 block을 이어붙여서 비문을 만들 것이다. 언급했던 것처럼 block size는 AES에서 128bits(=16bytes)다.

그런데 우리는 input값과 output값 연관관계를 줄이기 위해 행렬을 통한 연산을 수행할 것이다. 그 단위를 state라고 칭하고 이는 4X4의 행렬형태이다. 행렬 원소 하나에 1byte씩 들어가며, 그 순서는 컬럼 순서이다.

$a_{ij}$를 i행 j열이라고 하면

$a_{00}$ $\rarr$ $a_{10}$ $\rarr$ $a_{20}$ $\rarr$ $a_{30}$ $\rarr$ $a_{01}$ $\rarr$ $a_{11}$ $\rarr$ $a_{12}$ $\rarr$ ... $\rarr$ $a_{33}$

이렇게 세로의 순서를 가진다.

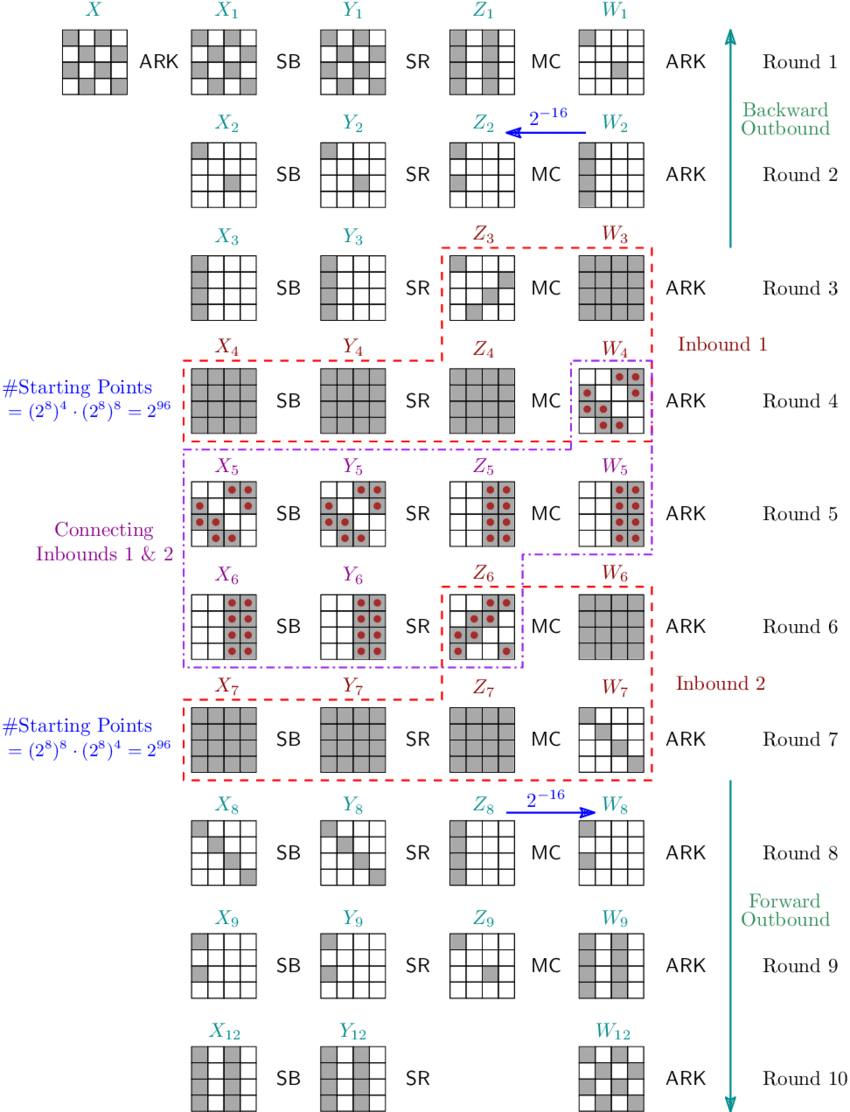
출처: https://www.researchgate.net/figure/A-Differential-Trail-for-10-Round-AES-256_fig3_350491744

그림을 먼저 보면 굉장히 어지럽다. 하나씩 알아보자. 우선 ARK가 11번, MC가 9번 일어나는 것은 인지하자.

4 stages

ARK: AddRoundKey

제일 쉬운 부분이다. 그냥 state와 key를 각 자리에 대해 XOR연산하면 된다. bit단위로 계산한다.

SB: Substitute bytes

S-box를 사용한 바이트 단위 대체하는 과정이다.

S-box가 뭐냐? 모든 바이트 경우에 대한 대체값을 지정한 테이블.
결국 시저사이퍼처럼 바이트가 대체되는 값이 같다. 그럼 원리는 무엇인가?

1. input으로 넣은 byte의 역원을 구한다($GF(2^8)$). 여기서 modulo는 $x^8+x^4+x^3+x+1$이다. 역원은 Extended Euclidean을 사용하면 된다.
2. 구한 역원을 $V$라고 하면 $W$를 구해야한다. $W=AV+B$인데 여기서 행렬 A와 벡터 B는 NIST표준에서 정한 고정값이다. 참고로 모듈러 연산을 하기 때문에 플러스, 마이너스 연산은 XOR과 같다.
3. 구한 W값이 대체할 값이다.

이 부분은 Field 중 갈로아 필드에 대한 이해가 없으면 무슨 말인지 모를 것이다. 선행으로 이해하고 오자.

왜 곱셈에 대한 inverse를 사용했을까?

Rationale
사실 라운드의 4가지 과정 전부가 암호학 공격에 대한 내성을 위한 것이다. 인풋의 bit 하나가 아웃풋의 랜덤한 위치의 bit에 영향을 미치게 하기 위한 것이다. 특히 SB는 1bit가 바뀌면 곱셈에 대한 역원을 계산하는 과정에서 1byte 전체에 영향을 미치게된다. 따라서 중간에 곱셈에 대한 역원을 활용한 것이다.

그럼 S-box만 알아도 되는가?

사실 그렇다. 모든 경우의 수에 대한 아웃풋이 정해져 있기 때문에 S-box를 통해 look up 한번이면 계산이 끝난다.

SR: ShiftRows

이름 그대로 행을 섞는 과정이다.

1. 0행을 그대로
2. 1행은 왼쪽으로 한칸 이동
3. 2행은 왼쪽으로 두칸 이동
4. 3행은 왼쪽으로 세칸 이동

이해가 어렵지는 않다.

해당 과정 역시 입력값이 조금 변해도 블록의 모든 값에 영향을 주기 위한 과정이다. 추후에 전체적인 그림을 통해 살펴볼 것이다.

MC: MixColumns

이 과정 역시 갈로아 필드 연산을 사용한다.

미리 정해진 행렬 4X4와 state를 우리가 아는 행렬곱으로 계산한다. 하지만 행렬곱을 할 때는 갈로아 필드 연산을 적용한다.

이 과정은 어떤 암호학 공격에 대한 저항을 가질까?

결과로 나온 행렬의 각 값은 state의 컬럼에 포함된 4개의 값의 영향을 받아 나온 값이다. 즉 state의 1bit만 바뀌었어도 state의 4byte가 영향을 받는다.

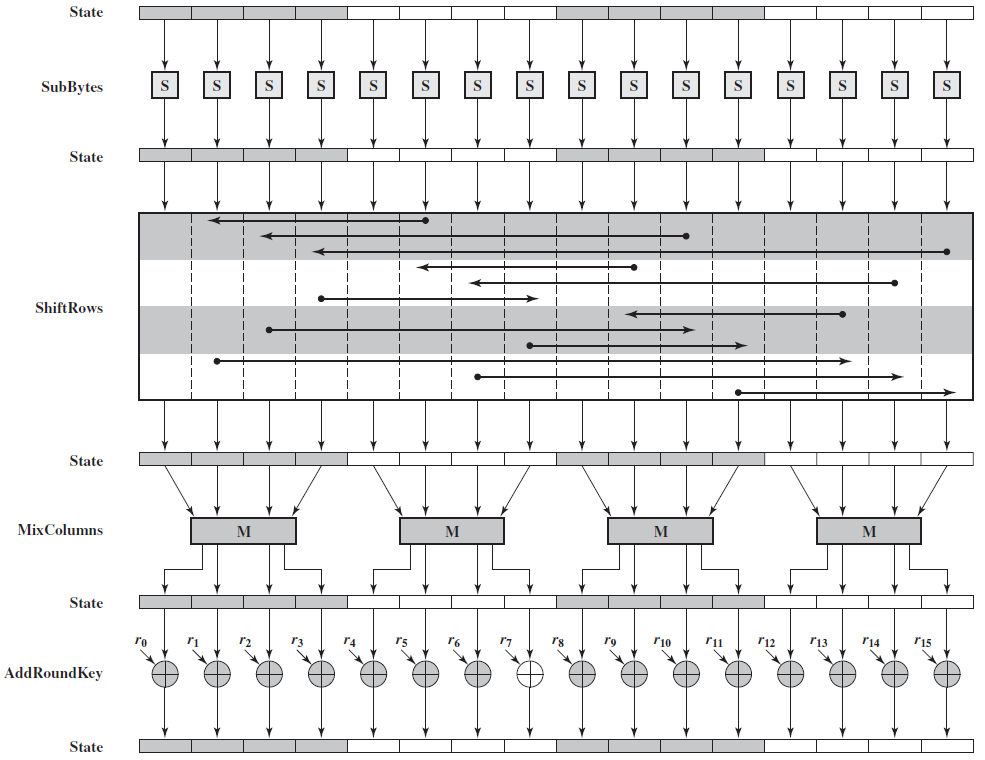
출처:https://commons.wikimedia.org/wiki/File:AES_Encryption_Round.png

Round 한개의 변환 과정이다.
이 그림을 통해 살펴보면 state의 1bit가 바뀌면 Round 1을 지나면 4byte가 바뀐다.

다시 이 결과값이 Round2를 통해 들어가는데 이 과정에서 모든 state에 영향을 미친다.

Key expansion algorithm

자 그럼 하나의 키를 가지고 어떻게 총 라운드 + 1개의 key를 생성하는가?

바로 key expansion algorithm을 사용한다.

출처:https://www.brainkart.com/article/AES-Key-Expansion_8410/

key 역시 state처럼 만들고 각 컬럼 단위 4bytes, 즉 1word를 기준으로 한다. 그림에서처럼 마지막 워드를 가지고 g함수를 돌리는데 Round처럼 shift row, substitution word를 한번 씩 해준다. 그리고 마지막으로 RC와 XOR 연산을 하는데 다음과 같다.

$RC_1=00000001$
$RC_2=00000010$
$RC_3=00000100$
$RC_4=00001000$
$RC_5=00010000$
$RC_6=00100000$
$RC_7=01000000$
$RC_8=10000000$
$RC_9=00011011$
$RC_10=00110110$

이것 역시 $GF(2^8)$을 이용한다.

참고로 AES-192, AES-256에서는 일련의 과정을 통해 128bits의 값만 가져온다.

정리

block cipher와 갈로아 필드에 대한 이해가 필요한 내용이었다. 과정이 굉장히 복잡해보이지만 프로그래밍 연산 난이도는 그렇게 높지 않다고 한다. 생각해보면 S-box도 256bytes의 4개의 테이블만 가지고 있으면 되니 1KB가 필요하다. 나머지 과정도 이미 정해진 값을 이용해 shift와 xor연산만 수행하면 되기 때문에 만드는게 개념을 이해하는 것보다 힘들지 않을 것 같다. 이 모든 과정에서 key만 바뀌는 것이고 round에서는 정해진 연산을 수행한다. 하지만 round가 평문의 내용 하나가 바뀌어도 절반 정도의 비문의 내용이 바뀌는 결과를 만든다. 이를 통해 암호학적 공격에 대한 방어도가 굉장히 높아진다. 현재에도 AES로 암호화가 이루어진다고 하니 굉장히 의미있는 공부가 됐다.