공유키 암호화 방식으로 RSA에 대해 알아봤고 이번 시간에는 3가지 다름 공유키 암호화 방식에 대해 알아보자.

• Diffie-Hellman key exchange
• Elgamal cryptographic system
• Elliptic Curve Cryptography

Diffie-Hellman Key Exchange

DLP

배경으로 이산수학을 조금 알고 있어야 한다.

Discrete Logarithm Problem

p가 소수일 때 modulo를 p라고 하면 p이하의 숫자 중에서 a의 지수가 1부터 p-1까지일 때 서로 다른 수라고 하면 이를 generator 혹은 primitive root of p라고 한다.

예를 들어, p가 19라고 하면 다음 그림과 같다.

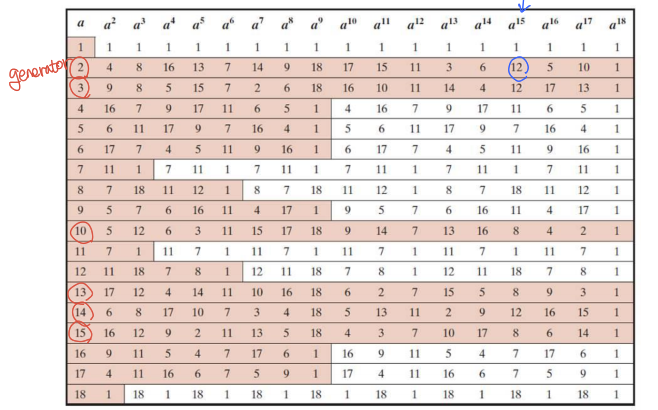
여기서 소수 p에 대한 primitive root는 2,3,10,13,14,15라고 할 수 있다.

그래서 discrete logarithm problem이 뭐냐?

generator 혹은 primitive root of p를 a라고 정하고 나서 b라는 값이 주어지면

$a^k \, mod \, \, p = b$

k값을 찾는게 바로 discret logarithm problem이다.

그래서 뭐야?

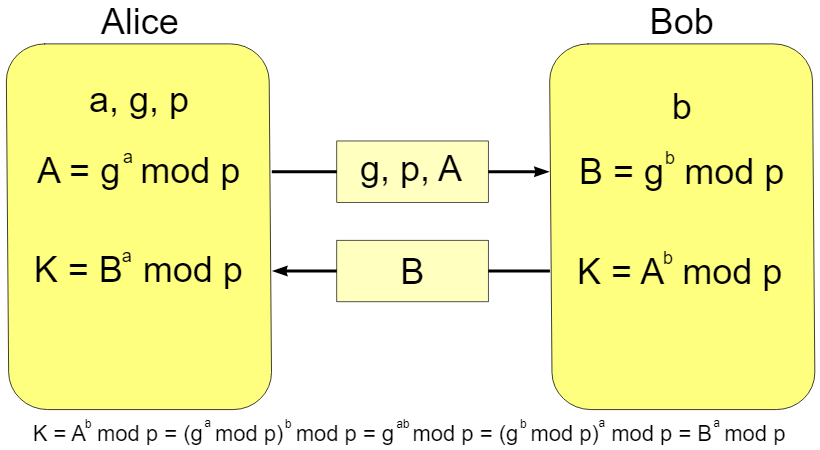
그림에서 g가 p의 generator이다.

키를 교환할 필요가 있을 때마다 한 사이클을 session이라고 보자.

session마다 각자 개인키와 공유키를 생성할 필요가 있다.

그래서 왼쪽 사용자는 개인키를 a를 정하는데 p보다 작은 값을 정하고 p의 generator인 g의 지수에 넣으면 그 값을 세션의 공유키 A라고 할 것이다.

반대편 사용자 역시 동일한 과정을 진행한다. 그럼 반대편 사용자의 세션 개인키는 b, 세션 공유키는 B가 된다.

키 생성이 끝나면 서로 자신의 공유키를 상대방에게 전송한다.

상대방의 공유키를 받으면 그 공유키의 지수에 자신의 세션 개인키를 넣는다.

그럼 결과적으로 $g^{ab} \, mod \, \, p$로 동일한 결과값을 갖게 되고 이제 이 값이 해당 세션에서 나와 상대방이 갖는 secret key가 된다.

Forward Secrecy

아까부터 세션이라는 단어를 사용했는데, Diffie-Hellman이 RSA에 비해 key exchange에서 더 안전한 점을 제공한다.

RSA에서는 공유키 {e,n}과 개인키 {d,n}을 세션마다 바꾸는 것이 아니다. 따라서 한 세션에서 누군가의 개인키가 유출되면 이전의 세션에 대해 공격자가 모두 들춰볼 수 있다.

반면에 DF는 세션마다 필요한 개인키, 공유키를 생성하므로 각 세션의 연관관계는 없다. 그리고 RSA는 DF방식에 비해 개인키, 공유키 생성이 비싸므로 DF처럼 세션마다 키를 생성하는 것이 어렵다.

이 안전성을 forward secrecy라고 한다.

MitM

Man in the Middle attack을 뜻한다.

DF방식은 유용하지만 만약 중간에 공격자가 끼어들어 두 사용자와 각각 키를 공유 교환하게 되면 이를 막을 방법이 없다.

뒤 챕터에서 배우겠지만 올바른 상대로부터 온 것인지 검증하는 기능이 필요하다.

Elgamal Cryptosystem

DF와 같이 DLP를 사용한다. 유사하지만 encryption, decryption 과정에서 차이가 있다.

p: prime number
g: g < p인 generator
a: private key, a < p - 1
A: $A=g^a \, mod \, \, p$
공유키: [p, g, A]
개인키: a

encryption

plaintext : M
k : k < p인 랜덤 정수 선택
K : $K=A^k \, mod \, \, p$
$C_1$ : $C_1=g^k \, mod \, \, p$
$C_2$ : $C_2=KM \ mod \ p$
ciphertext : ($C_1$,$C_2$)

decryption

ciphertext : ($C_1$,$C_2$)
calculate K : $K=(C_1)^a \ mod \ p$
plaintext : $M=C_2K^{-1} \ mod \ p$

이전에 배운 one-time pad를 XOR 대신 곱셈으로 바꾼 것과 비슷하다.

ECC

Elliptic Curve Cryptography

$y^2=x^3+ax+b$

위와 같은 형태를 가진 곡선을 기반으로 한다.

$Q=dP$

위 식이 의미하는 바가 무엇인가.

ECC에서 DLP와 비슷한 ECDLP(Elliptic Curve Discrete Logarithm Problem)이 있다.

기본적으로 곡선에서 P점이 있다면 P의 접선을 그린다. 이 접선과 만나는 곡선의 다른 점이 있고 이 점의 x값이 같은 또 다른 점을 2P라 한다.

비슷하게 2P로부터 시작해서 같은 과정을 거치면 그 점을 3P라고 한다.

그런데 재미있는 점은 기존의 Discrete Logarithm Problem과 마찬가지로 같은 점을 가르키는 d값이 존재한다는 것이다.

많은 것을 생략하긴 했지만 이게 ECDLP이다.

기존의 암호학에서 제곱 연산을 곱셈 연산으로, 곱셈 연산을 덧셈 연산으로 바꾸면 완전 비슷한 모양을 가진다.

Diffie-Hellman 타원곡선형 버전이다.

더욱 더 재미있는 점은 ECDLP가 기존의 DLP보다 같은 비트수 대비 높은 안전성을 제공한다는 점이다. (Pollard rho 방식의 공격에서)

나중에 다시 언급하겠지만 DLP문제를 더 쉽게 해결하는 GNFS(General Number Field Sieve)가 ECDLP에서는 먹히지 않는다.