
주변에서 쉽게 볼 수 있는 문제중의 하나로 소수 구하기 알고리즘을 알아보자.
1. 소수란?
소수는 1 또는 자기 자신만을 약수로 가지는 수를 의미한다.
즉, 1과 자기 자신외에는 어떤 수도 나눌수 없어야한다. 여기서 주의할점은 1은 소수가 아니라는 점이다.
2. 소수를 구하는 방법
소수를 구하는 방법에는 3가지 정도를 들 수 있다.
2.1 나눠보기
가장 직관적인 방법이 아닐까 싶다. 일반적으로 시간복잡도를 요하지 않는 문제의 경우 항상 이방법으로 코드를 짠다. 가장 간단하기 때문에..
2부터 N-1까지 루프를 돌면서 나눠보는 방법이다.
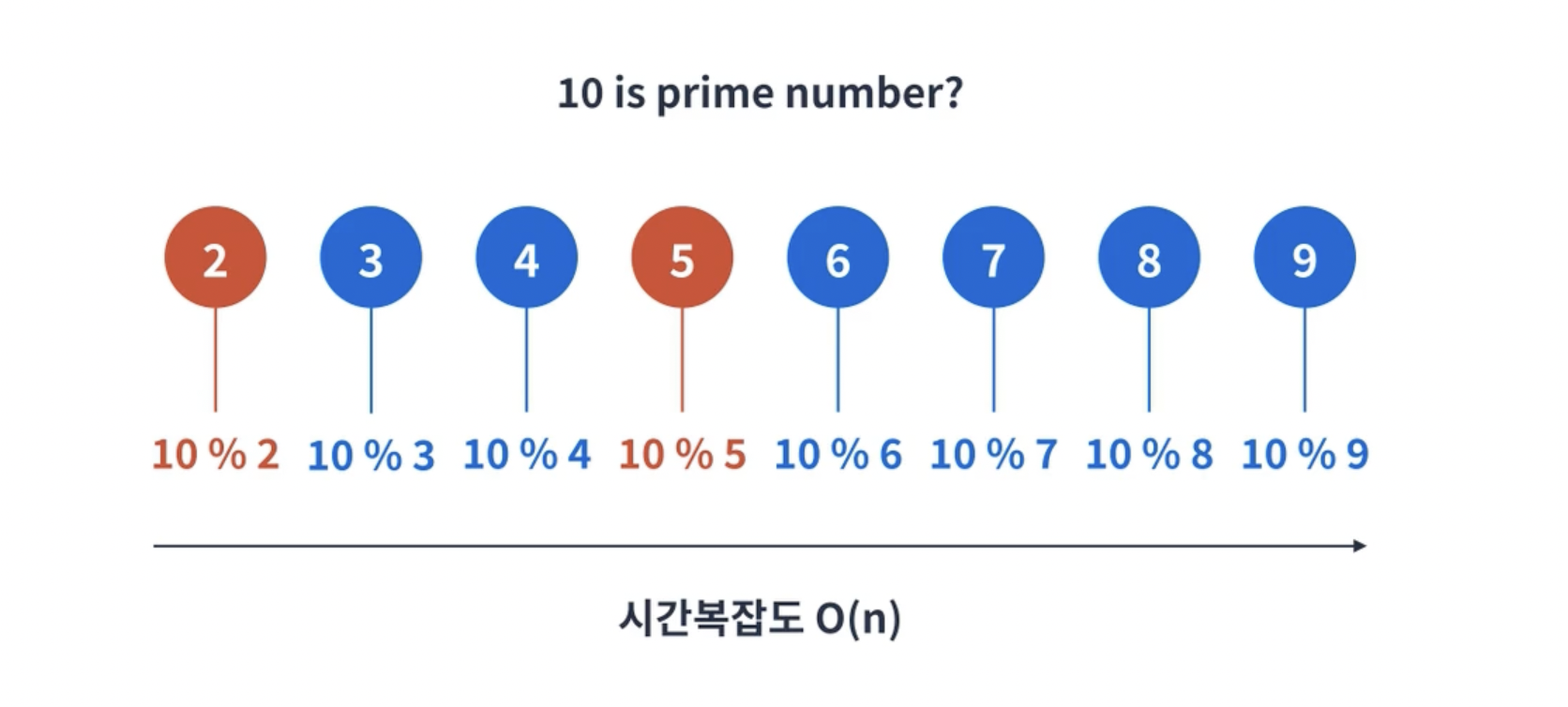
코드로 구현해보자.
2.2 효율성 개선
2.1의 알고리즘은 n이 늘어날수록 시간이 늘어나는 o(n)의 시간 복잡도를 가지고 있기 때문에 매우 느리다.
이를 조금만 개선해서 시간복잡도를 향상시켜보자.
어떤 소수도 N의 제곱근보다 큰 수로 나눠지지 않는다는 규칙이 있다.
예를 들면, 17이 소수인지 확인해보려면 4까지만 확인해보면 된다.
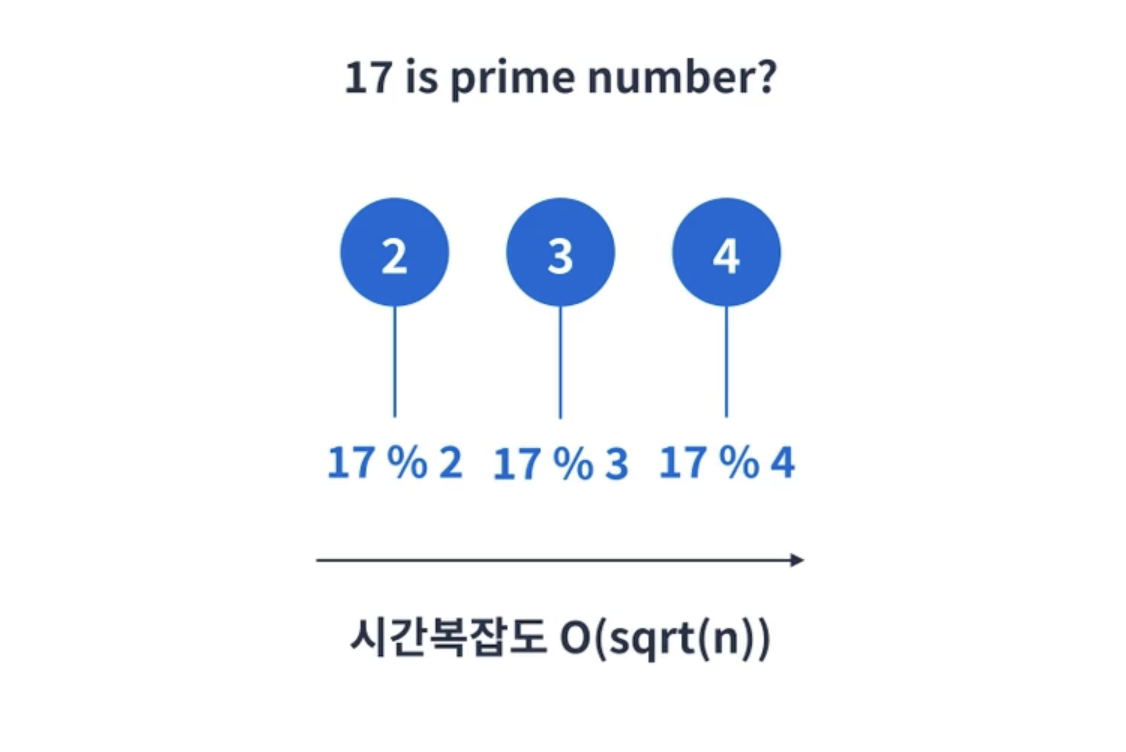
코드로 구현해보자.
function isPrime(num) {
for(let i = 2; i * i <= num; i++) {
if(num % 1 == 0) {
return false;
}
}
return true;
}3.3 에라토스테네스의 체
고대 그리스 수학자 에라토스테네스님께서 발견한 소수를 찾는 방법이다. 소수를 찾는 방법 중 가장 효율성이 좋기 때문에 가장 많이 사용된다.
처음 즉, 2부터 주어진 숫자까지의 소수를 구할 때 아주 유용하다.
2부터 순회를 하면서 2의 배수를 모두 지워주고, 3부터 순회를 하면서 3의 배수를 모두 지워주고, 4는 이미 지워졌으니 패스하고, 5의 배수를 지우고.. 주어진 수의 제곱근까지만 확인해보면 끝난다.
이런식으로 지워나가면 지워지지 않는 수들은 소수라고 할 수 있겠다.
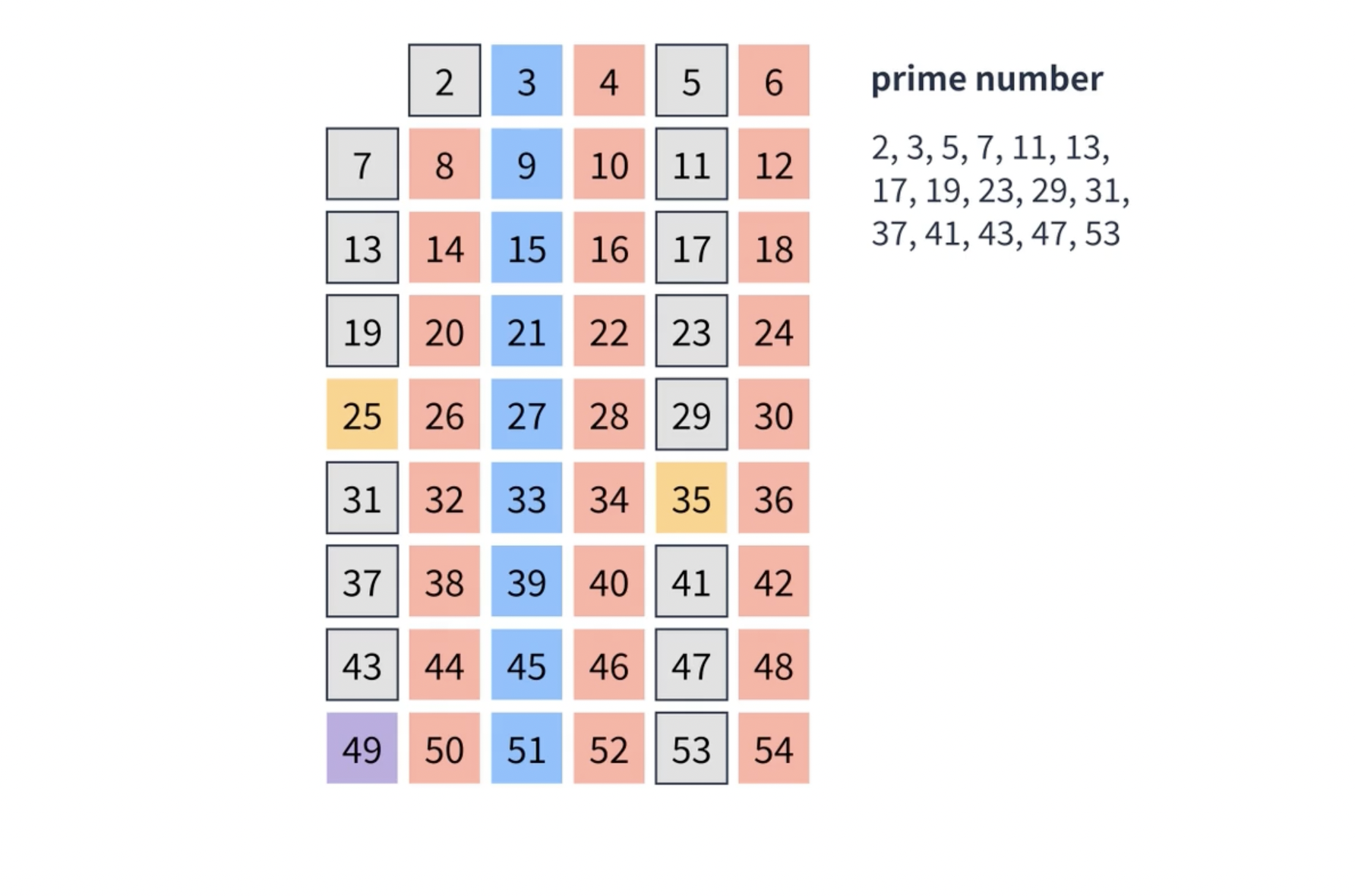
코드로 구현해보자.
function solution(n) {
// 0이 포함되기 때문에 입력받은 수보다 하나 크게
const arr = Array.from({ length: n + 1 }).fill(true);
arr[0] = arr[1] = false;
const sqrt = parseInt(Math.sqrt(n));
for (let i = 2; i <= sqrt; i++) {
if (arr[i] === true) {
for (let j = 2; i * j <= n; j++) {
arr[i * j] = false;
}
}
}
return arr.filter((v) => v === true).length;
}