1. 점근 표기법
점근 표기법이란?
알고리즘의 성능을 수학적으로 표기하는 방법, 알고리즘의 “효율성”을 평가하는 방법
점근 표기법의 종류에는
빅오(Big-O)표기법, 빅 오메가(Big-Ω) 표기법이 있습니다.
빅오 표기법은 최악의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지,
빅오메가 표기법은 최선의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지에 대해 표기합니다.
예를 들어
"빅오" 표기법으로 표시하면 ,
"빅 오메가" 표기법으로 표시하면 의 시간복잡도를 가진 알고리즘이다!
라고 표현할 수 있습니다.
첫 번째 방법
input = [3, 5, 6, 1, 2, 4]
def is_number_exist(number, array):
for element in array: # array 의 길이만큼 아래 연산이 실행
if number == element: # 비교 연산 1번 실행
return True
return False
result = is_number_exist(input)
-
위에서 연산된 것들을 더해보면, 이렇게 총 N * 1의 시간 복잡도를 가진다는 걸 볼 수 있습니다.
그런데 여기서, 모든 경우에 N 만큼의 시간이 걸릴까요? -
input = [3, 5, 6, 1, 2, 4] 이라는 입력값에 대해서 3을 찾으면,
첫 번째 원소를 비교하는 순간!! 바로 결과값을 반환하게 됩니다.
즉, 운이 좋으면 1번의 연산 이후에 답을 찾을 수 있다는 의미입니다. -
그러나, input = [4, 5, 6, 1, 2, 3] 이라는 입력값에 대해서 3을 찾으면 어떻게 될까요?
마지막 원소 끝까지 찾다가 겨우 마지막에 3을 찾아 결과값을 반환하게 됩니다.
즉, 운이 좋지 않으면 input의 길이(N) 만큼 연산 이후에 답을 찾을 수 있습니다. -
이처럼, 알고리즘의 성능은 항상 동일한 게 아니라 입력값에 따라서 달라질 수 있습니다.

-
빅오 표기법으로 표시하면 ,
빅 오메가 표기법으로 표시하면 의 시간복잡도를 가진 알고리즘 -
알고리즘에서는 거의 모든 알고리즘을 빅오 표기법으로 분석합니다.
왜냐면 대부분의 입력값이 최선의 경우일 가능성은 굉장히 적을 뿐더러,
우리는 "최악의 경우"를 대비해야 하기 때문입니다.
2. class
class Cloth {
constructor(color, size, price) {
this.color = color
this.size = size
this.price = price
}
printInfo() {
console.log(`색깔: ${this.color}, 사이즈: ${this.size}, 가격: ${this.price}`)
}
}
const shirts = new Cloth('white', 'M', '50000')
const coat = new Cloth('navy', 'L', '200000')
shirts.printInfo()
coat.printInfo()- 출력 결과

참고자료
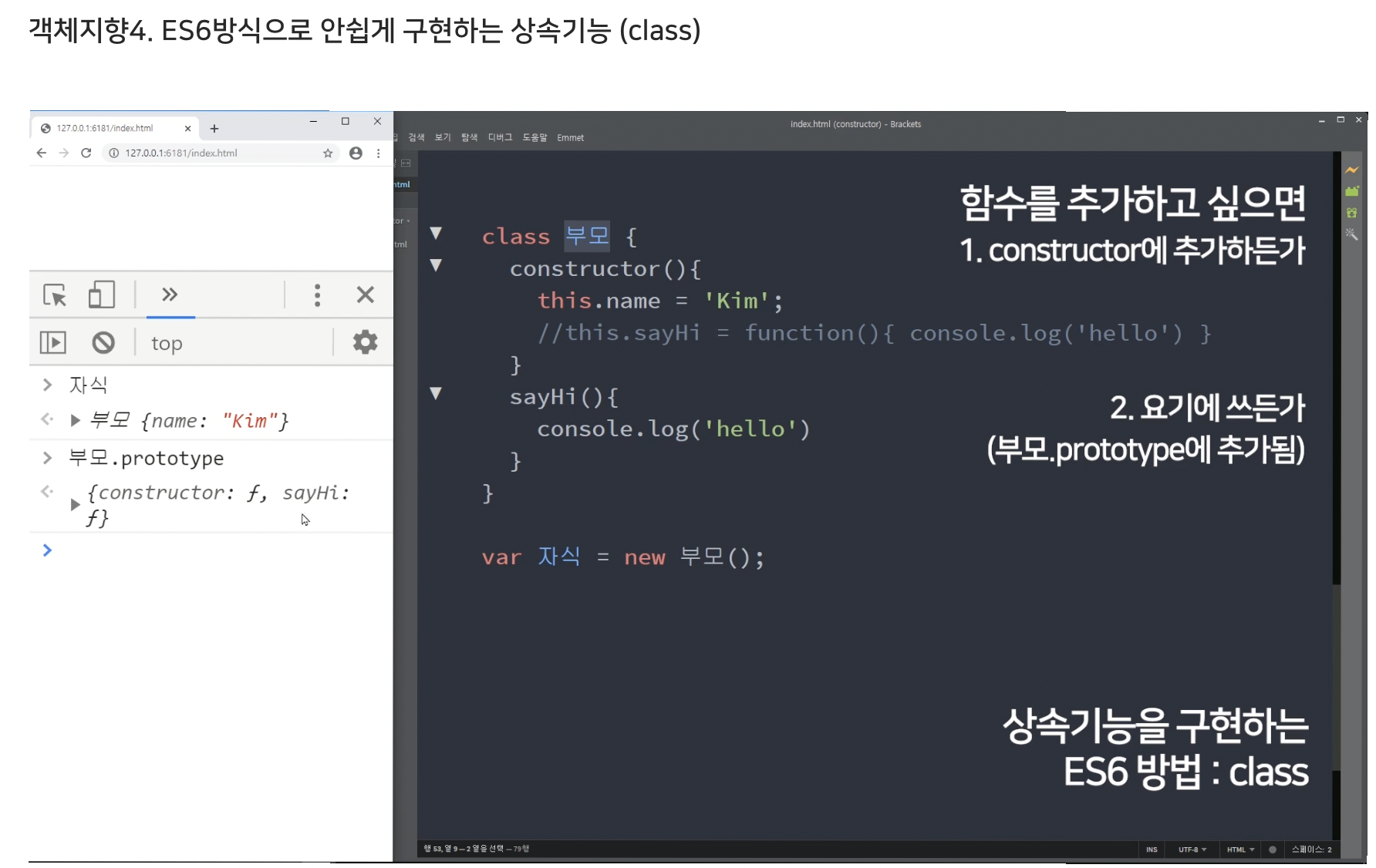
- 응용