스택
(c++의 stack 기준으로 작성됨)
<stack>헤더, std 네임스페이스 안에 있다. (stack은 c++ 표준 라이브러리이다)
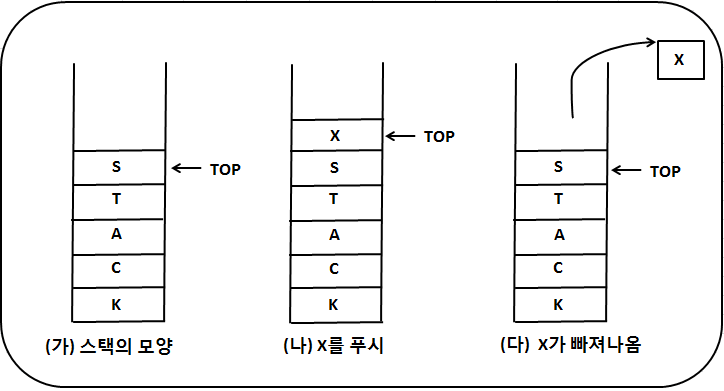
LIFO(last in first out)이다.
container adaptor이다. 즉, 다른 container 클래스의 기능을 제한해서 만들어졌다. (벡터를 생각해보면 이해된다)
복잡도
시간복잡도는 일반적인 상황 ( 크기 재설정 후 재배치 하는 상황등은 제외한 일반적인 상황)
을 가정했다.
Space complexity of Stack : O(n).
| 작업 | time complexity | space complexity |
|---|---|---|
| pop | O(1) | O(1) |
| push | O(1) | O(1) |
| top | O(1) | x |
| size | O(1) | x |
용례
- DFS 알고리즘
- 운영체제에서 쓰레드 및 모든 프로세스들은 다 스택을 가지고 있음
- 재귀 알고리즘
큐
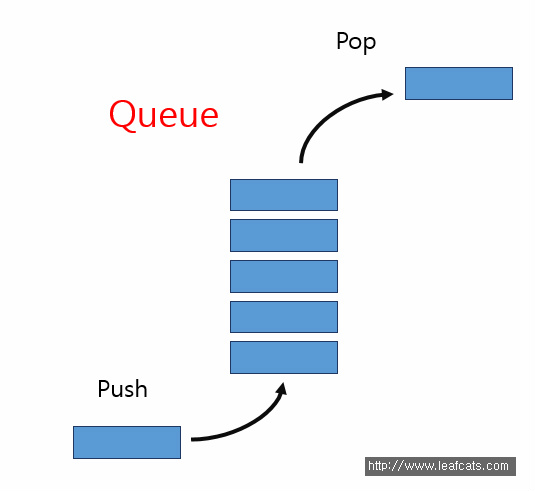
container adaptor이다.
<queue>헤더, std 네임스페이스에 있음.
FIFO (first in first out)임.
복잡도
Queue space complexity is O(n).
| 작업 | time complexity | space complexity |
|---|---|---|
| front | O(1) | x |
| pop | O(1) | O(1) |
| push | O(1) | O(1) |
용례
- BFS 알고리즘
- 프로세스 간의 통신에 사용, js가 비동기 처리할 때에도 사용.
힙
설명
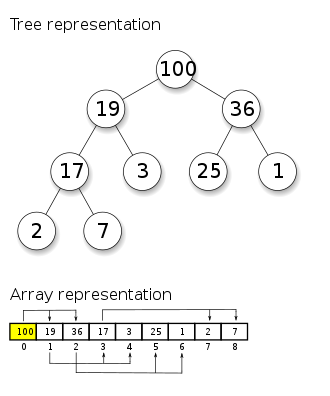
최대/최소 값을 가장 빠르게 찾는 자료구조.
힙은 구현시, 가능하면 Array를 이용해서 구현하는 것이 가장 공간을 적게 사용한다.
또한, 특성인 부모노드가 자식노드의 값보다 크다만 만족하면 어떤 구조이든 상관이 없다.
c++ 기준 make_heap이라는 함수를 쓰고, 이 함수를 이용해서 heap이 사용할 container를 넣는다.
priority_queue 를 쓰는것이 좀더 편한듯하다.
vector<int> v( vector<int> {1,6,5,2,3,8,4,9,7 });
make_heap(v.begin(), v.end());
이후 설명의 편의성을 위해
1. 최대 값을 기준으로 진행.
2.완전 이진 트리(complete binary tree)를 기준으로 설명.
힙의 특성
부모노드가 자식노드의 값보다 커야함.
method 동작 방식
https://www.geeksforgeeks.org/heap-using-stl-c/
복잡도
space complextiy : O(N)
| 작업 | time complexity |
|---|---|
| insert | O(logN) |
| find_max | O(1) |
| delete_max | O(logN) |
용례
- priority queue ( 거의 힙 그대로 사용한다 )
- Dijkstra's algorithm
