백준의 원과 좌표 관련 두 문제를 정리하면서 무엇이 핵심이었는지 알아본다.
두 문제 모두 계산에 필요한 좌표와 원의 중심 좌표, 원의 반지름이 주어진다.
주어진 요소들을 적절한 식을 통해 풀어야 한다.
공통적으로 필요한 계산
두 좌표 사이의 거리
두 좌표 사이의 거리는 피타고라스 정리를 통해 간단하게 구할 수 있다.
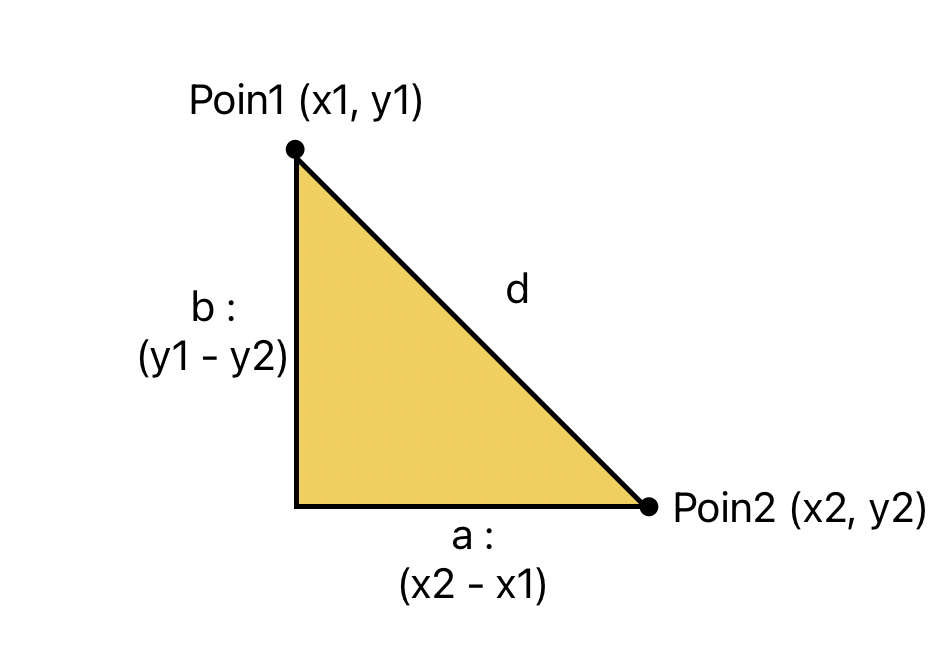
d^2 = a^2 + b^2
각 문제에 필요한 계산
1002. 터렛
터렛 문제는 원의 테두리의 교점이 몇개 존재하는지를 알아내야 한다.
원이 어떻게 접하는 지에 따라 조건문을 설정해 풀 수 있다.
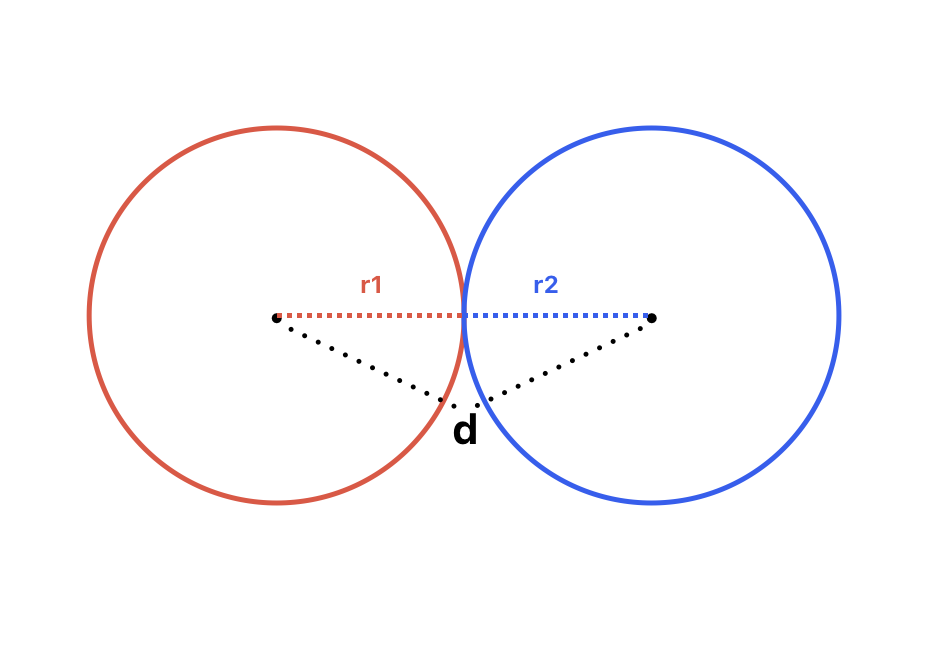
- 두 원이 외접하는 경우
두 원의 반지름의 합은 두 원의 중심점 사이의 거리와 같다.r1 + r2 = d
교점은 하나다.
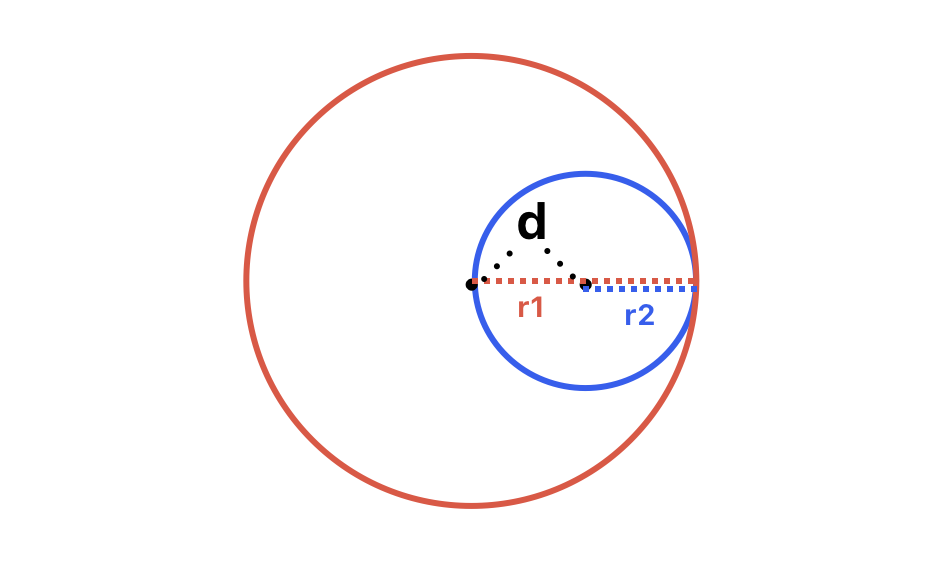
- 두 원이 내접하는 경우
두 원의 반지름의 차는 두 원의 중심점 사이의 거리와 같다r1 - r2 = d
교점은 하나다.
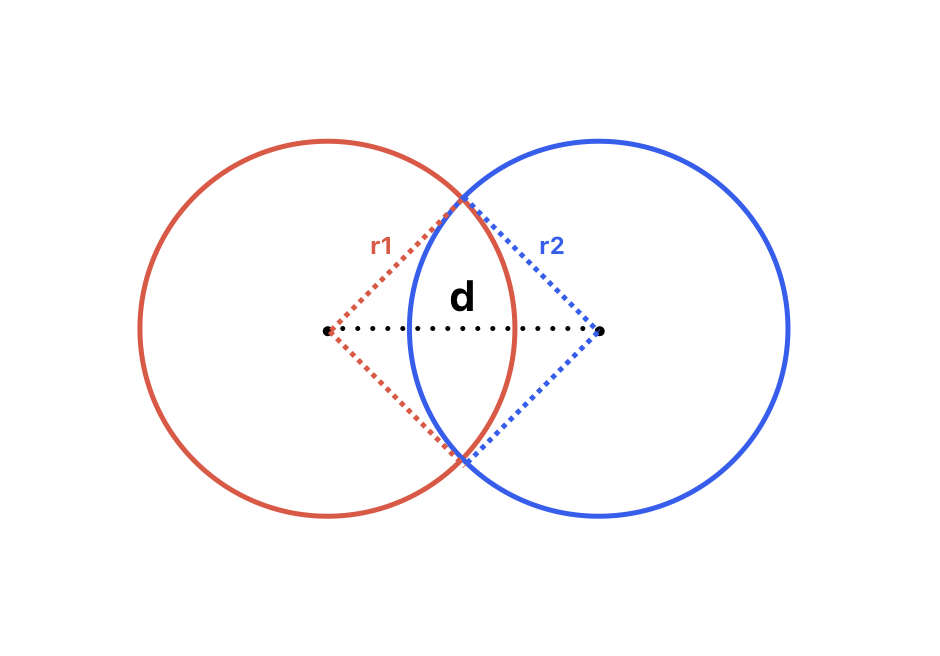
- 두 원이 교차하는 경우
두 원의 반지름의 합은 두 원의 중심점 사이의 거리보다 크고,
두 원의 반지름의 차는 두 원의 중심점 사이의 거리보다 작다r1 + r2 > d
r1 - r2 < d
교점은 둘이다.
- 두 원이 접하지 않는 경우
두 원의 중심점 사이의 거리가 0보다 클 경우 두 원의 반지름의 합보다 크다.
두 원의 중심점 사이의 거리가 0일경우 두 원의 반지름의 차보다 작다.(d > 0) r1 + r2 < d
(d = 0) r1 - r2 > d
교점은 없다.
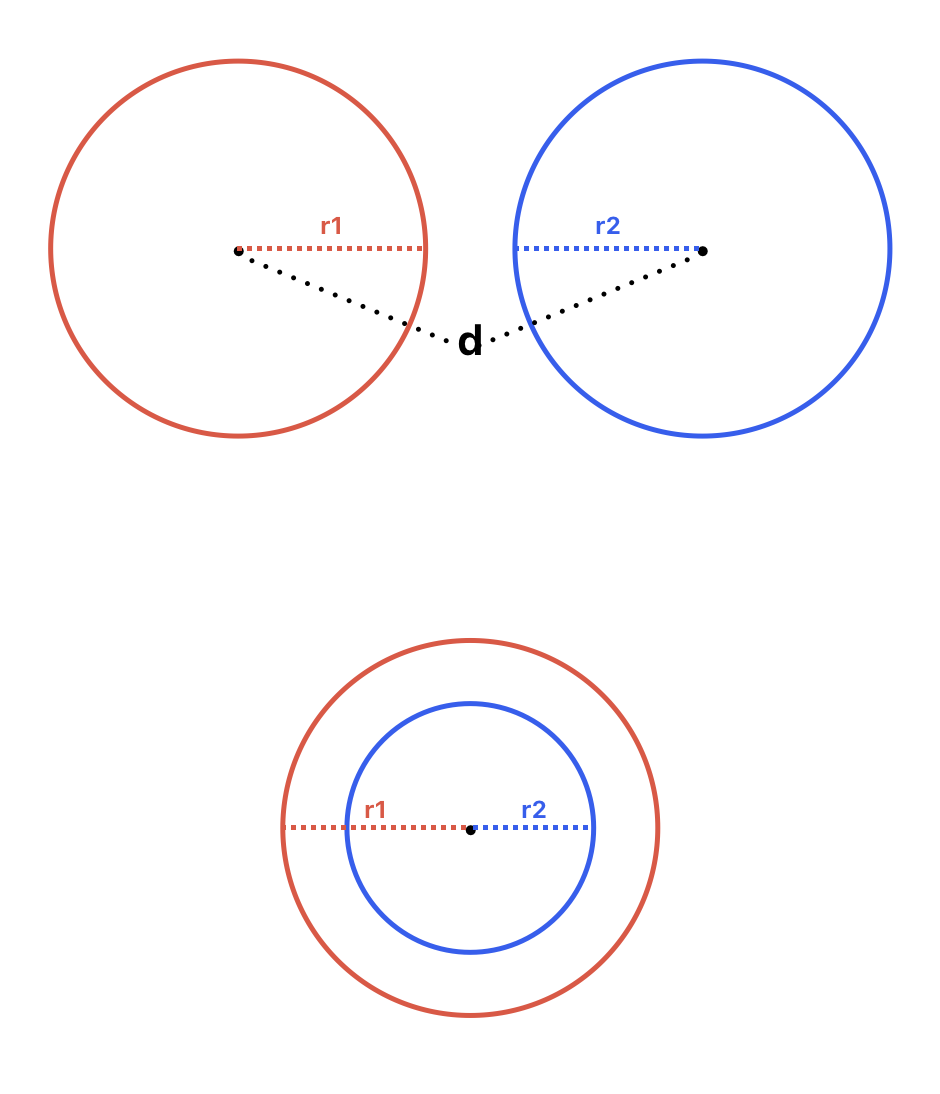
- 두 원이 같을 경우
두 원의 중심점 사이가 0이고, 두 원의 반지름은 같다.(d = 0) r1 = r2
교점은 무한하다.

const [n, ...inp] = require('fs').readFileSync('/dev/stdin').toString().trim().split('\n')
let result=[];
for(let i=0; i<n; i++) {
let [x1,y1,r1,x2,y2,r2] = inp[i].split(' ').map(Number)
const sum =(r1+r2)**2;
const diff =(r2-r1)**2;
const d =(x1-x2)**2 + (y1-y2)**2;
if (d<sum && d>diff) {
result.push(2);
} else if (d===sum || (d===diff && d!==0)) {
result.push(1);
} else if (d<diff || d>sum) {
result.push(0);
} else if (d===0) {
if (r1===r2) {
result.push(-1);
} else {
result.push(0);
}
}
}
console.log(result.join('\n')1004. 어린왕자
어린왕자의 이동경로중 최소한으로 행성을 들르는 경우를 구하는 문제로 행성 테두리에 접하는 경우는 없다.
어린왕자는 행성을 피해 다니기에 출발점과 도착점이 행성 안에 존재하는 지를 구하는게 핵심이다.
출발점과 도착점이 주어진 행성 하나하나의 반지름 보다 작은 경우만 구하면 된다.
start(x1, y1), end(x2, y2), planet(cx, cy)
- 출발점이나 도착점 중 하나만 원 안에 있을 경우
행성에 들른다.(x1 - cx) + (y1 - cy) < r
And(x2 - cx) + (y2 - cy) > r
(x1 - cx) + (y1 - cy) > rAnd(x2 - cx) + (y2 - cy) < r
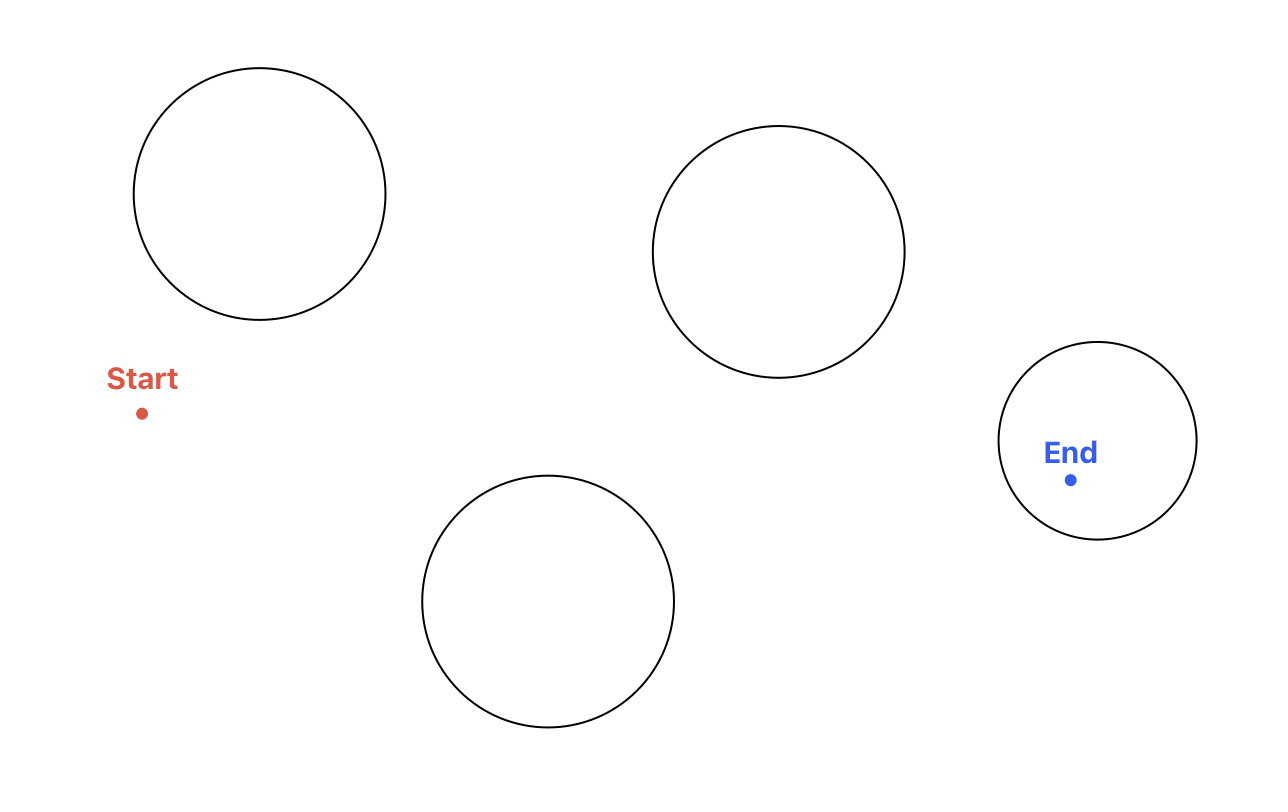
- 출잠점과 도착점 둘 다 원 밖에 있을 경우
행성에 들르지 않는다.(x1 - cx) + (y1 - cy) > r
And(x2 - cx) + (y2 - cy) > r
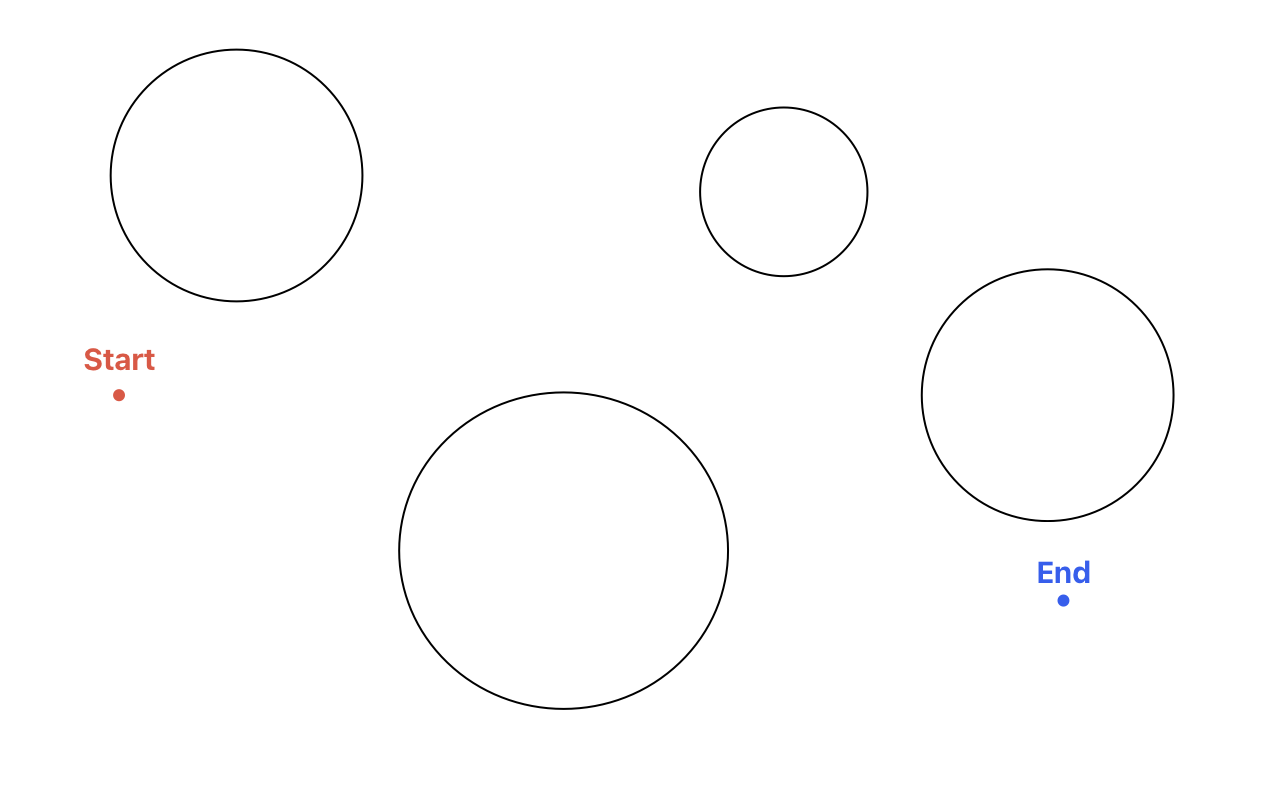
- 출발점과 도착점 둘 다 원 안에 있을 경우
행성을 들르지 않는다.(x1 - cx) + (y1 - cy) < r
And(x2 - cx) + (y2 - cy) < r
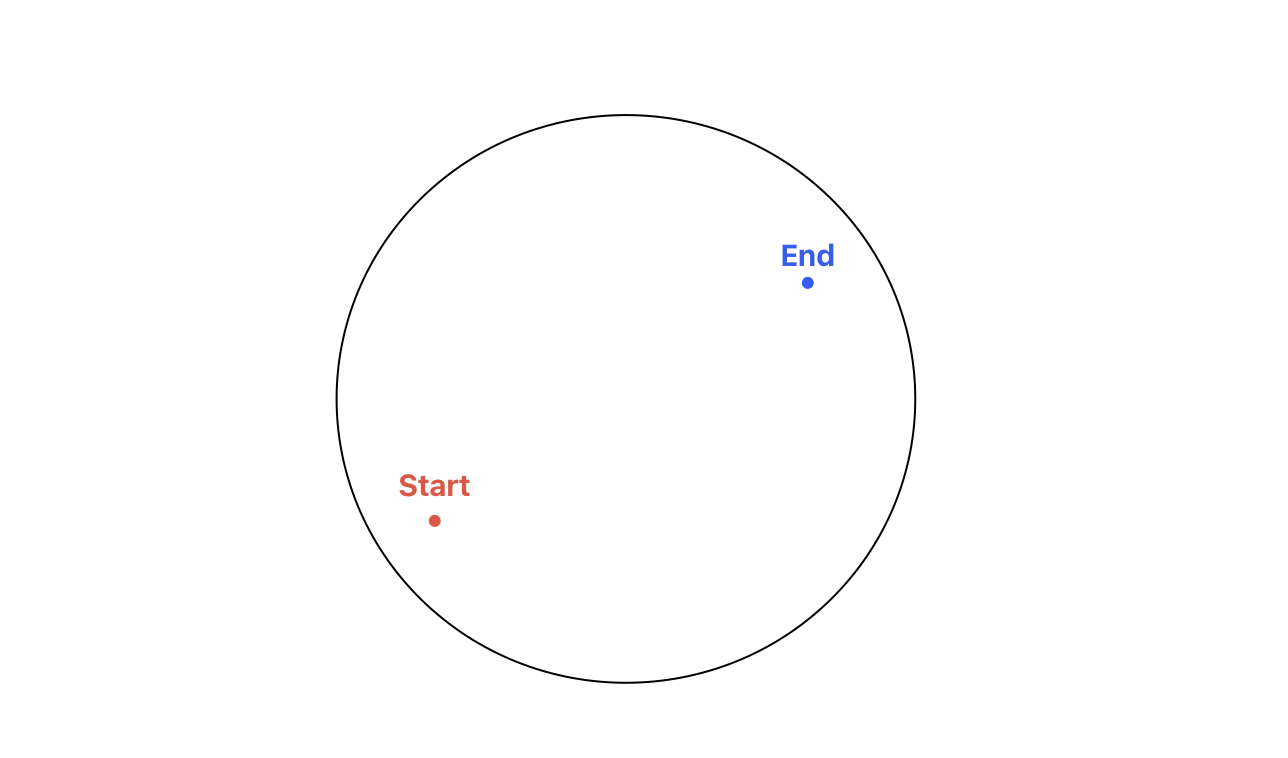
const [t,...inp] =require('fs').readFileSync('/dev/stdin').toString().trim().split('\n')
let idx=0;
let result=[];
for(let i=0; i<t; i++) {
let count=0
let n=Number(inp[idx+1])
let [x1,y1,x2,y2] = inp[idx].split(' ').map(Number)
let arr=inp.slice(idx+2,idx+n+2)
idx+=n+2
for(let j=0; j<n; j++) {
let [cx,cy,r] = arr[j].split(' ').map(Number)
if((x1-cx)**2+(y1-cy)**2<r**2&&(x2-cx)**2+(y2-cy)**2>r**2) count++
if((x1-cx)**2+(y1-cy)**2>r**2&&(x2-cx)**2+(y2-cy)**2<r**2) count++
}
result.push(count)
}
console.log(result.join('\n'))