목차

• 알고리즘과 평가
• 하테나 다이어리의 키워드 링크
• 하네타 북마크의 기사 분류

알고리즘 실용화

알고리즘과 평가

데이터 규모와 계산량 차이

반복해서 언급해왔듯이, 대상이 되는 데이터가 크면 클수록 알고리즘이나 데이터 구조 선택이 속도에 영향을 미칩니다.

간단한 탐색만 하더라도 순차적으로 찾아가는 선형탐색은 O(n)의 시간만큼, 바이너리 서치는 O(logn)만큼의 시간이 소비되게 됩니다.

알고리즘이란?

알고리즘이란 무엇인가?에 대해 다시 생각해봅시다.

• 넓은 의미에서의 알고리즘

  • 데이터를 적절하게 처리하고 결과를 출력하는 전체적인 구조 즉, 도메인 로직

• 좁은 의미에서의 알고리즘

  • 적당한 값을 입력하면 명확하게 정의된 계산절차에 따라 값이 출력으로 반환되는 것

알고리즘을 배우는 의의

CPU나 메모리 등의 컴퓨터 자원은 유한하고 개발자 및 컴퓨터쟁이들은 이를 어떻게든 풀로 땡겨서 활용하고자 합니다.

따라서 좀 더 최적의 수행방법을 통해 문제를 푸는 것이 모든 엔지니어들이 추구하는 바이자. 알고리즘이라는 것은 이 엔지니어들의 공통언어입니다. 과거 엔지니어가 쌓아온 알고리즘을 알고있는 것 만으로도 새로운 문제에 대처할 수 있을 것입니다.

알고리즘의 평가

O(n), O(logn)과 같이 Order표기를 사용하는 것이 일반적입니다.

각종 알고리즘을 Order표기하면 아래와 같은 계산량이 자주 나타납니다.

• O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n)

이런 계산량 개념은 시간뿐만 아니라 공간적인 양에서도 사용됩니다. 즉, 실행시간이나 단계 횟수뿐만 아니라 메모리 사용량을 논할 경우에도 Order표기가 사용된다는 것입니다.

알고리즘과 데이터 구조

알고리즘 서적을 보면 알고리즘과 데이터 구조는 알고리즘 + 데이터 구조와 같이 세트로 다루어지는 경우가 많습니다. 이는 알고리즘이 자주 사용되는 조작에 맞춰 데이터 구조를 선택할 필요가 있기 떄문입니다.

예를들어 사전에 적절한 트리구조로 데이터를 저장해두면, 대개의 경우는 탐색처리를 단순화할 수 있어 계산량을 줄일 수 있습니다.

또한 RDBMS에서는 B+트리라는 트리구조가 자주 사용되고 이를 통해 디스크 I/O 및 탐색 단계를 줄일 수 있습니다.

알고리즘에서 자주 사용하는 조작에 맞춰 데이터 구조를 알잘딱깔센 합시다.

계산량과 상수항

계산량의 Order표기법에서는 상수항을 무시합니다. 예를 들어 if문으로 분기하거나, 일차 변수를 확보하는 등의 간단한 처리가 해당됩니다.

구현이 복잡하지 않더라도 CPU캐시에 올리기 쉬운지, 분기예측이 발생하지 않는지 등 계산량의 구조적인 특성에 의존하는 형태로 상수항에서 차이가 나는 경우도 있습니다.

이런 상수항에서의 예로 정렬 알고리즘을 이야기할 수 있습니다. 이론적으로는 O(n log n)이 하한으로 해당 시간복잡도를 가진 정렬알고리즘을 여러개 있습니다. 하지만 그 중 가장 빠른것은 퀵정렬이라고 합니다. 이는 특성상 CPU캐시를 사용하기 쉽다는 장점이 있어서 시간적인 측면에서 유리하게 작용합니다.

줄일 수 있으면 상수항도 줄여서 구현 합시다.

하지만 상수항을 줄이기 위해 처음부터 최적화를 수행하는 것은 대체로 잘못된 방침입니다. 계산량 O(n^2) 알고리즘의 상수항을 아무리 줄여봤자. O(n log n)인 알고리즘이 있다면 후자를 사용하는 편이 개선효과가 더 클것 입니다.

추측하지 말고 계측하라라는 말이 있습니다. 알고리즘을 교체해서 개선해야 할 것인지, 상수항을 줄여서 개선해야 할 것인지, 물리적 리소스가 부족해서 하드웨어를 교환해야 할 것인지 판단하는 것 모두 계측에서 시작됩니다.

하테나 다이어리의 키워드 링크

키워드 링크란?

하테나 다이어리에서는 키워드 링크라는 서비스를 제공합니다. 이는 블로그에 글을 작성하면 키워드에 자도응로 링크가 달리는 기능입니다.

입력한 내용에 대해 27만 단어를 포함하는 키워드 사전과 매칭하여 필요한 부분에 <a>를 삽입하여 텍스트를 치환하는 기능을 제공합니다.

최초 구현 방법

이를 구현하기 위한 최초 구현방법은 단순 정규표현을 활용해 구현하는 것이였습니다.

foo, bar, baz와 같은 단어를 OR로 잇는 정규표현식으로 나타내면 다음과 같습니다.

(foo|bar|baz|....)

이를 코드로 표현하는 다음과 같습니다.

책에서 활용하는 언어를 모르기에.. 필자가 익숙한 코틀린으로 변환하여 다시 작성하였습니다.

fun wrapWithAnchorTag(input: String): String {
    val words = listOf("foo", "bar", "baz")
    val regex = words.joinToString("|").toRegex()

    return input.replace(regex) {
        """<a href="/keyword/${it.value}">${it.value}</a>"""
    }
}

fun main() {
    val text = "foo is a programming language, bar and baz are common examples."

    val result = wrapWithAnchorTag(text)
    println(result)
}

서비스가 커져버렸다.

키워드는 사용자가 등록하는 것이므로 오픈한 당시에는 그다지 어휘수도 많지 않고, DB에서 그때그때 정규표현을 만들어서 키워드 링크하는 식의 여유로운 처리로 작동했습니다. 하지만 키워드수가 많아짐에 따라 문제가 발생했습니다. 정규표현 처리에 시간이 걸리는 것입니다.

이런 정규표현구현에 오토마톤 방식을 활용합니다. 이는 앞서 본 (foo|bar|baz)와 같은 패턴매칭을 앞에서부터 입력값을 살펴가면서 매칭에 실패하면 다음 단어를 시도하고, 또 실패하면 그 다음 단어를 시도하는 단순한 방법으로 진행됩니다. 그 결과 키워드의 개수에 비례하는 계산량이 소비됩니다.

정규표현을 -> Trie 매칭 구현 변경

하테나는 따라서 정규표현을 기반한 방법에서 Trie를 활용한 방식으로 구현을 변경했습니다

Trie란??

Trie는 트리구조의 일종인 데이터 구조입니다. 탐색대상 데이터의 공통 접두사를 모아서 트리구조를 이루는 게 특징입니다.

다음은 {"rebro", "replay", "hi" , "high", "algo"} 를 트라이 구조로 표현한 사진입니다.

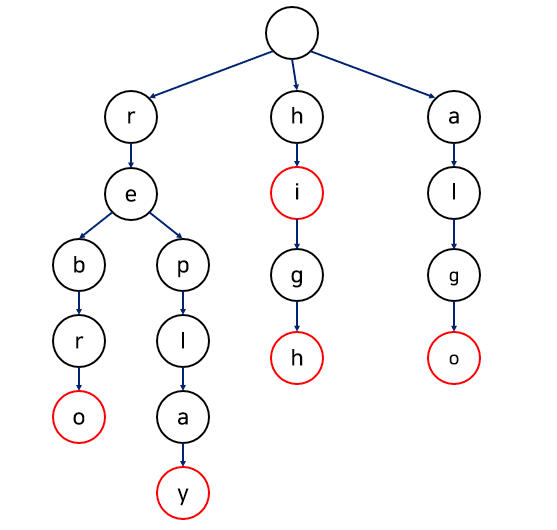
이 Trie구조를 사전과 비교하면서 패턴매칭을 하면 정규표현인 경우보다 계산량을 줄일 수 있습니다. 입력문서를 Trie에 입력한 다음, 엣지를 순회하면서 종단이 발견되면 해당 단어가 포함되어 있는 걸로 간주하는 것입니다.

위의 그림에서 success라는 단어를 생각해보면 s라는 문자열이 포함되어 있지 않으므로 매칭되지 않음을 알 수 있습니다. 정규표현이 패턴매칭에 비해 확실히 적은 순회횟수임을 알 수 있습니다.

이후 하테나는

이후 하테나 다이어리는 거대한 정규표현 -> Trie를 활용한 방법 -> Regexp::List방식을 활용한 방법으로 발전하게 됩니다. 이 과저에서 알게된 점이 몇 개 있습니다.

• 초기 심플한 구현이었던 것이 유효했다.

  • 간단한 정규표현으로 구현했을 때에는 간단해서 구현도 쉽고, 유연성이 풍부했다. 따라서 이후 Trie구조로 변경하는 것 도 용이했습니다.

• 데이터가 커짐으로써 문제가 혼재화하는 경우가 있습니다.

  • 캐시 등 표면적인 방법으로는 어느정도 문제를 회피할 수 있었으나, 최종적으로 알고리즘이 갖는 근본적인 문제점을 해결해야만 했습니다. 이러한 통찰에는 이전에 말했듯 계산량읙 관점에서 문제를 포착할 필요가 있습니다.

처음부터 최적의 구현을 사용하는 것이 반드시 옳다고는 할 수 없습니다. 데이터가 작은 동안에는 오히려 결과가 좋았을 수도 있고, 데이터가 대규모가 될 시기를 대비해 본질적인 문제를 인지하고 있으면 충분합니다.

하네타 북마크의 기사 분류

기사 분류란?

하테나의 기사 분류란 기사 내용을 기반으로 기사의 카테고리를 자동으로 분류하는 기능입니다. 새로운 기사가 사용자에 의해 작성되면 하테나의 시스템은 해당 기사의 내용(단어의 빈도수 등)을 통해 카테고리를 판정합니다.

이 판정과정은 베이지안 필터링에 의해 판정됩니다. 베이지안 필터는 텍스트 문서 등의 입력을 통해 나이브 베이즈라는 알고리즘을 적용해 해당 문서가 어느 캬테고리에 속하는지를 판정하는 프로그램입니다.

특징적인 것은 미지의 문서의 카테고리 판정을 수행함에 있어서 과거에 분류가 끝난 데이터의 통계정보로부터 판정을 수행한다는 것입니다.

즉 학습 데이터 셋을 기반으로 패턴인식을 통해 카테고리를 분류합니다.

베이지안 필터링의 원리

베이지안 필터의 핵심은 나이브 베이즈라는 알고리즘입니다.

나이브 베이즈에서의 카테고리 추정은 특정 문서 D가 주어졌을 떄 이 문서가 확률적으로 어떤 카테고리 C에 속하는게 가장 그럴 듯 한가를 구하는 문제입니다.

즉 문서, D가 주어 졌을 때 카테고리 C의 조건부 확률을 구하는 문제입니다.

P(C|D)

여러 카테고리 중 이 확률이 가장 높은 값을 나타낸 C가 최종적으로 선택되는 카테고리가 됩니다.

이 조건부 확률을 직접 계산하는 것은 어려운일이지만, 베이즈의 정리에 따라 계산가능한 식으로 변형할 수 있습니다.

P(C|D) = P(D|C) * P(C) / P(D)

변형하면 다음과 같이 되고, 우변의 각 확률을 구하는 문제로 변형됩니다.

• P(D) : 문서 D가 발생할 확률인데 이는 모든 카테고리에 대해 동일한 값으로 결과를 비교할 경우에는 무시할 수 있습니다.
• P(C) : 특정 카테고리가 출현할 확률을 의미합니다. 이는 학습 데이터 중 여러 데이터가 어떤 카테고리로 분류되었는지 그 횟수를 저장해 사용합니다.
• P(D|C) : 문서 D라는 것은 임의의 단어 W가 연속해서 출현하는 것으로 간주하여 P(D|C) => P(W1|C) P(W2|C) P(W3|C) ... 같은 식으로 근사할 수 있습니다.

따라서 문서 D를 단어로 분할하고 단어마다 어느 카테고리로 분류됐는지 그 횟수를 보존해두면 카테고리를 추론할 수 있습니다.

즉 나이브 베이즈에서는 데이터가 주어지면 해당 데이터가 사용된 횟수나 단어 출현 횟수와 같이 간단한 수치만 저장해두면 나중에 확률만 계산하면 카테고리를 추정할 수 있다는 것입니다.

알고리즘이 실용화되기까지

베이지안 필터링의 구조는 의외로 심플하며, 실제로 구현해도 200줄 이내로 구현이 가능할 정도입니다.

이제 이를 어떻게 실용화하는지를 나열해 보겠습니다.

1. 분류 엔진을 개발합니다. + 서버로 올립니다.
2. 이 서버와 통신해서 결과를 얻는 클라이언트를 작성하고, 웹 클라이언트에서 호출합니다.

이 두 과정으로 동작은 하지만 뒷배경에는 다음과 같은 역할이 더 필요합니다.

• 학습 데이터를 정기적으로 백업할 수 있도록 데이터 덤프/ 로드 기능을 추가합니다.
• 학습 데이터를 1,000건 정도 수작업으로 준비합니다.
• 바람직한 정밀도가 나오는지 추적하기 위한 통계 구조를 작성합니다.
• 다중화를 고려하여 스탠바이 시스템을 구성합니다. (자동 장애 극복 기능 작성)
• 웹 어플리케이션에 필요한 사용자 인터페이스를 마련합니다.

이와 같이 실무에서 고려해야하는 점은 상당히 많은걸 확인할 수 있습니다.

수비 자세, 공격 자세

저자는 다음과 같이 말합니다.

• 수비 자셰 : 동일한 알고리즘이라도 대규모 데이터를 빠르게 정렬하거나 검색, 압축하는 일은 아무래도 발생하는 문제를 얼마나 잘 맞아들이는가에 대한 수비적인 자세에서 자주 사용하는 알고리즘입니다.

• 공격 자세 : 기계학습이나 패턴인식등은 적극적으로 대규모 데이터를 응용하고 그 결과에 따라 어플리케이션에 부가가치를 추가한다는 의미입니다.

중요한 것은 수비를 하든 공격을 하든간에 어느 정도 기본 지식을 익혀두는 것이 중요합니다. Trie가 어떤 데이터인지 그 특성을 모르면 적용할 수 없을 것이며, 베이지안 필터와 같은 원리를 이해하지 않으면 문서를 자동으로 분류한다는 발상을 할 수 없을 것입니다.