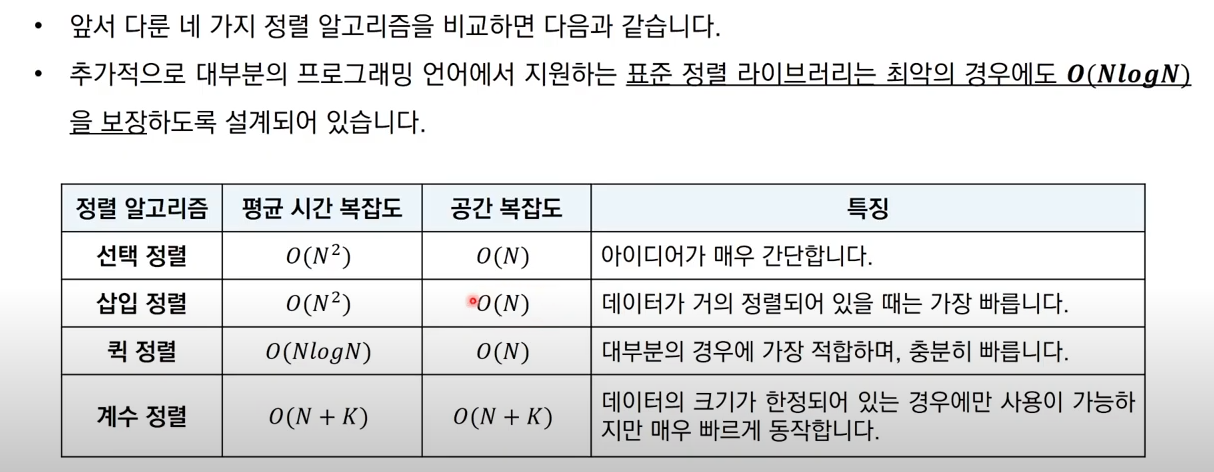
선택정렬
기본개념 :
인덱스가 i부터 시작하여 i~len(array)까지의 최소값과 index i을 비교하여 바꾼다.
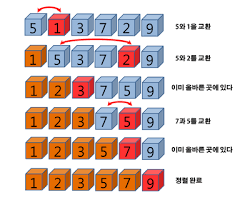
array = [7,5,9,0,3,1,7,2,4,8]
for i in range(len(array)):
min_index = i #가장 작은 인덱스
for j in range(i+1, len(array)):
if array[min_index] > array[j]:
min_index=j
array[i],array[min_index] = array[min_index], array[i]시간복잡도는 N + N-1 + N-2 + .... 2
즉 (N^2 + N) / 2 임으로 간략하게 O(N^2)으로 나타낼 수 있다.
이는 버블정렬 O(N^2)와 동일한 정도이다.
N=100
N=1000
N=10000 일때 소요시간
선택정렬
- 0.0123
- 0.354
- 15.475
퀵정렬
- 0.00156
- 0.00343
- 0.0312
기본정렬라이브러리
- 0.00000753
- 0.0000365
- 0.000248
기본정렬라이브러리 그는 '빛' 그 자체....
삽입정렬
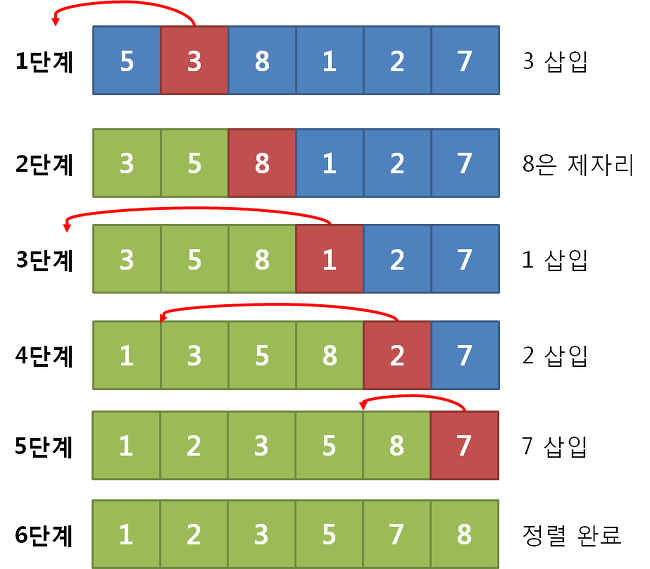
1단계부터 선택된 숫자의 왼쪽은 이미 정렬되어있다고 판단하고 숫자가 들어갈 곳에 집어 넣는다.
소스:
array = [7,5,9,0,3,1,6,2,4,8]
for i in range(1, len(array)):
for j in range(i,0,-1):
if array[i] < array[j-1]:
array[i], array[j-1] = array[j-1], array[i]
else:
break
시간복잡도는 최대 O(N^2)이며 리스트가 거의 다 정렬되어 있을때는 O(N)까지 줄어든다. 이미 정렬되어있는 데이터에 쓰기 좋음.
퀵정렬
복잡하고도 빠른 정렬방법
리스트 내에서 첫원소를 피벗데이터로 삼고, 왼쪽부터 피벗보다 큰 데이터, 오른쪽부터 피벗보다 작은 데이터를 선택해서 위치를 교환한다. 계속하다 엇갈리면 작은 데이터와 큰 데이터를 서로 교환하는 방법



왼쪽과 오른쪽 리스트에도 똑같이 정렬을 실시
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while left <= right:
# 피벗보다 큰 데이터를 찾을 때까지 반복
while left <= end and array[left] <= array[pivot]:
left += 1
# 피벗보다 작은 테이터를 찾을 때까지 반복
while right > start and array[right] >= array[pivot]:
right -= 1
if left > right: # 엇갈렸다면 작은 데이터와 피벗을 교체
array[right], array[pivot] = array[pivot], array[right]
else: # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
array[left], array[right] = array[right], array[left]
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1) # 재귀함수
quick_sort(array, right + 1, end)
quick_sort(array, 0, len(array) - 1)
print(array)파이썬다운 코드인데 시간복잡도가 늘어난 듯?
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소 (리스트 슬라이싱)
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분 (리스트 컴프리헨션)
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
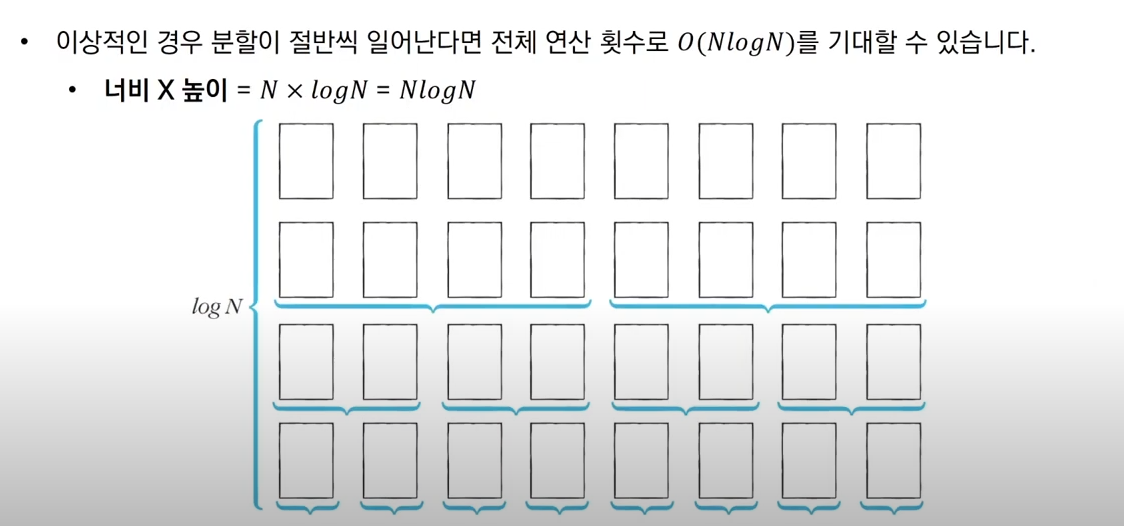
print(quick_sort(array))시간복잡도는 O(NlogN)이며 퀵정렬은 모든 원소가 정렬되어 있을때 최악의 성능을 발휘한다. (삽입정렬과 정반대)
계수정렬
데이터 크키 k만큼의 리스트를 만들고 그냥 때려박아서 더하는 방법
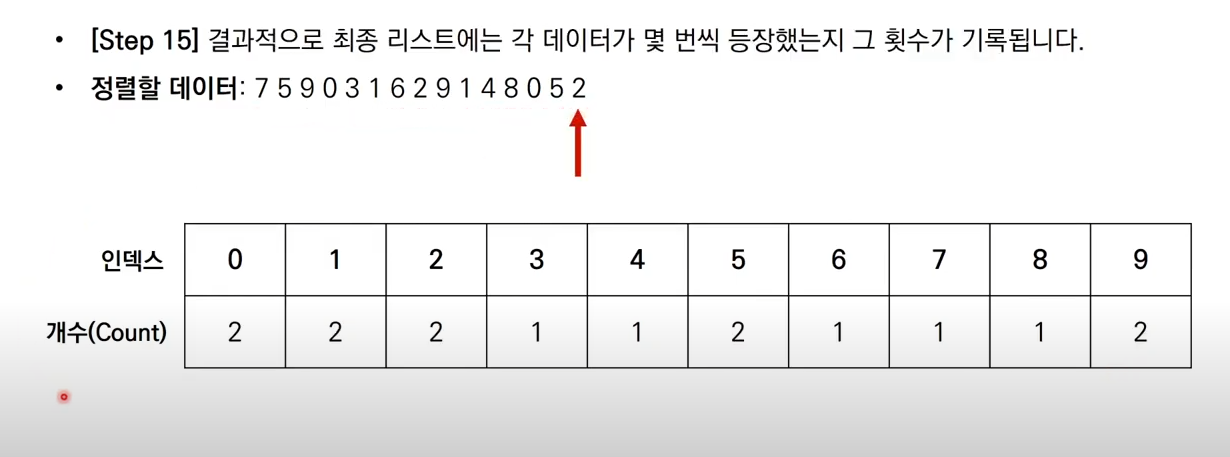
0이 2개, 1이 2개, 2가 2개...해서 모든데이터를 리스트에 더하고 출력하면 끝
소스코드
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화)
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
-
k가 클때는 메모리를 많이 잡아먹음
-
데이터가 1,10000 단 2개가 있을 때는 비효율적이다.
-
데이터가 최대 k일때 O(n+k)의 시간복잡도를 가진다.
정렬 시간복잡도 정리