다익스트라(Dijkstra)

다익스트라(Dijkstra)

다익스트라 알고리즘은 가중치가 있는 그래프의 한 정점에서 다른 정점까지의 최단경로를 구하는 알고리즘이다.

대략적인 동작방법은 다음과 같다

1. 출발 정점이 가지는 최단 거리 값은 0, 이외의 모든 정점이 갖는 최단 거리 값은 무한대로 초기화한다.

2. 최단 거리 값이 가장 작은 정점을 찾는다.

3. 2에서 선택된 정점(A)은 방문기록을 갖게된다.

4. 2에서 선택된 정점과 인접한 모든 정점을 탐색한다.

5. 4에서 탐색된 정점 중 방문기록이 없는 정점을 검사한다.

6. 2에서 선택되었던 정점 A가 가지는 최단 거리 값에서, 5에서 검사하게 될 정점(B)까지의 거리 누적합이 B의 기존 최단 거리 값보다 작으면, 누적합 값으로 B가 가지는 최단 거리 값을 갱신한다.

7. 모든 정점을 방문할 때까지 2~6의 과정을 반복한다.

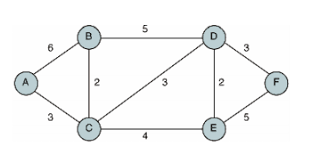
위 가중치 그래프를 통해 다익스트라 작동 순서를 확인해보자.

이때 출발점은 A로 지정하자

그리고 각 정점까지의 최단 거리 값과 방문 여부를 테이블로 표현해보자

정점	A	B	C	D	E	F
최단 거리	0	INF	INF	INF	INF	INF
방문여부	False	False	False	False	False	False

최단 거리 값이 가장 작은 정점은 A이다

이제 A와 인접한 정점의 거리 값을 갱신해보자

B는 방문하지 않았고, 0 + 6 < INF 이므로 6으로 갱신해준다
C도 같은 이유로 3으로 갱신해준다

정점	A	B	C	D	E	F
최단 거리	0	6	3	INF	INF	INF
방문여부	True	False	False	False	False	False

이제 방문한 정점을 제외하고 거리 값이 가장 작은 정점을 찾으면, C가 된다

C와 인접한 정점으로 A, B, D, E가 있다.

먼저 A는 이미 방문한 정점이므로 검사하지 않는다.

B의 경우, C가 가지는 거리 값 3에서 B로 가는 가중치 2를 더한 5는, B가 저장하고 있던 거리 값 6보다 적다. 따라서 B의 거리 값을 5로 갱신한다.

D의 경우, 3+3 < INF 이므로 갱신하고, E 또한 3+4로 갱신한다

정점	A	B	C	D	E	F
최단 거리	0	5	3	6	7	INF
방문여부	True	False	True	False	False	False

이 과정을 반복하며 최단 거리 값을 모든 정점을 방문할 때까지 반복한다

모두 완성하면 표는 다음과 같이 된다

정점	A	B	C	D	E	F
최단 거리	0	5	3	6	7	9
방문여부	True	True	True	True	True	True

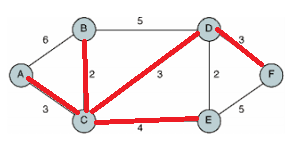
이렇게 완성된 표는 다음 그림과 같이 최단 경로로 각 정점에 도달하는 간선을 선택했을 때, 각 정점까지 최단 경로로 갈 수 있음을 의미한다

다익스트라 알고리즘의 최적화

$V$는 정점의 개수, $E$는 간선의 개수 라 하자

최단 거리 값이 가장 작은 정점을 찾을 때, 배열에서 찾으려 하면, 선형 탐색을 하게 되어 누적 된 결과, $O(V^2)$의 시간복잡도를 갖게 된다

따라서 이 부분에서 최소 값을 빠르게 찾아야하는데, 그 방법으로 우선순위 큐를 사용하는 것이다

우선순위 큐에서 한 번 값을 추출해 최솟값을 찾을 때마다 $O(logV)$의 시간이 나고, 누적 시행되는 결과 $O(ElogV)$의 시간복잡도를 갖게 된다!

거리를 기록하는 경우를 방문배열을 선언하지 않아도 되는 방법이 있다

우선순위 큐에서 꺼내게 된 정점으로부터 인접 정점까지의 거리를 갱신할 수 있는지 확인한다
그때, 갱신이 된다면 거리를 갱신하고 갱신된 정점에 대한 정보를 다시 큐에 넣어주면 된다

큐에서 최소 거리를 가진 원소를 pop해보자

그 다음 pop한 원소에는 특정 정점 $v$에서 가지게 된 최소 거리 $l$을 얻게 되는데, 만약 해당 정점 원소를 pop하기 직전에 다른 정점으로부터 $v$로 가는 최단거리가 갱신되어 $l$보다 더 작아진 상태를 생각해보자

그렇다면 방금 pop한 $l$의 최단거리를 갖는 $v$의 정보는 결국 쓸모없게 되는 것이다

큐에서 꺼낸 정점으로부터 인접 정점을 탐색하는 것이 불필요한 과정이 되는 경우가 존재하는 것이다

따라서 $v$의 인접 정점을 찾기 전에 정말로 $v$가 가지는 최단거리로 $l$을 유지하고 있는지 확인해 볼 필요가 있다

이 검사식이 없어도 풀리는 문제가 있지만, 고난도 문제는 시간 초과를 막기위해서라도 필수적이다
https://www.acmicpc.net/problem/17396