백준 11057번 - 오르막 수(★★ / O / 1) : Python

개요

• 풀이 시간 : 20분
• 시간 제한 : 1초
• 메모리 제한 : 256 MB
• 기출 : backjoon
• 링크 : https://www.acmicpc.net/problem/11057

문제

오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.

예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.

수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입력

첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력

첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

해결방법

문제 이해하기

이 문제는 특이하게도 맨 앞에 0이 와도 된다는 규칙이 있었다. 그리고 나서 한번 시뮬레이션해보자.

• N이 1이라면 : 0, 1, 2 ... , 8, 9 => 총 10개
• N이 2이라면
  • 맨앞이 0인경우 : 00, 01, 02, ..., 09 => 총 10개
  • 맨앞이 1인경우 : 11, 11, 12, ..., 19 => 총 9개
  • (...)
  • 맨앞이 9인경우 : 99 => 총 1개
  • 따라서 1 + 2 + 3 + ... + 10 = 55개
• N이 3이라면 마찬가지로 55 + (55-10) + (55-10-9) + ... + 1 = 220 이 나올것이라고 예측할 수 있다.

알고리즘

규칙성은 찾았다. 그렇다면 이 문제를 쉽게 풀려면 어떻게 해야할까? 이럴때는 간단한 표를 그려보고 시작하면 좋다.

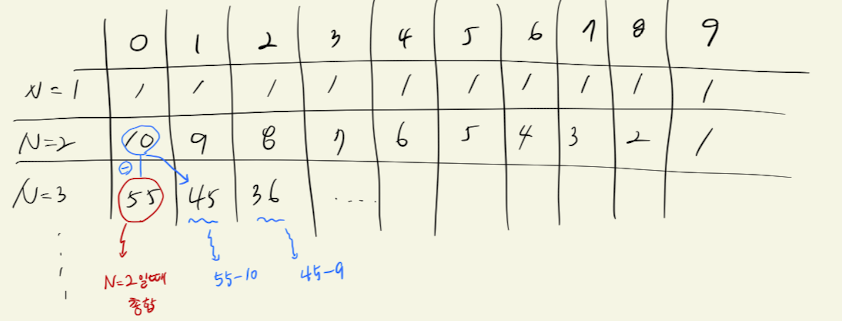
사실 처음에는 다이나믹 문제라고는 인지하지 못한채 표를 그러보고 채워보니까 쉽게 규칙성을 찾을 수 있었다. 이렇듯 특정 식을 통해 구할 수 없는 문제라면 다이나믹 방법으로 구해보는 것도 아주 좋은 해결책이 된다.

✍️ 만약 이전부터 다이나믹 프로그래밍 문제를 풀어보지 않았다면 이 문제도 어떤 식이 있는게 아닐까? 이러면서 계속 규칙을 찾고 있었겠지...

Python

내 코드

import sys

input = sys.stdin.readline

if __name__ == "__main__":
    n = int(input())
    dp = [[0] * 10 for _ in range(n)]

    for i in range(10):
        dp[0][i] = 1

    for i in range(1, n):
        sumTemp = sum(dp[i - 1][:])
        subTract = 0
        for j in range(10):
            dp[i][j] = sumTemp - subTract
            subTract += dp[i - 1][j]
    print(sum(dp[n - 1][:]) % 10007)

✍️ 오랜만에 쉽게 해결할 수 있어서 기분이 좋았다.