개요
- 풀이 시간 : 30분
- 시간 제한 : 2초
- 메모리 제한 : 512 MB
- 기출 : baekjoon
- 링크 : https://www.acmicpc.net/problem/13023
문제
BOJ 알고리즘 캠프에는 총 N명이 참가하고 있다. 사람들은 0번부터 N-1번으로 번호가 매겨져 있고, 일부 사람들은 친구이다.
오늘은 다음과 같은 친구 관계를 가진 사람 A, B, C, D, E가 존재하는지 구해보려고 한다.
- A는 B와 친구다.
- B는 C와 친구다.
- C는 D와 친구다.
- D는 E와 친구다.
위와 같은 친구 관계가 존재하는지 안하는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 사람의 수 N (5 ≤ N ≤ 2000)과 친구 관계의 수 M (1 ≤ M ≤ 2000)이 주어진다.
둘째 줄부터 M개의 줄에는 정수 a와 b가 주어지며, a와 b가 친구라는 뜻이다. (0 ≤ a, b ≤ N-1, a ≠ b) 같은 친구 관계가 두 번 이상 주어지는 경우는 없다.
출력
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
해결방법
문제 이해하기
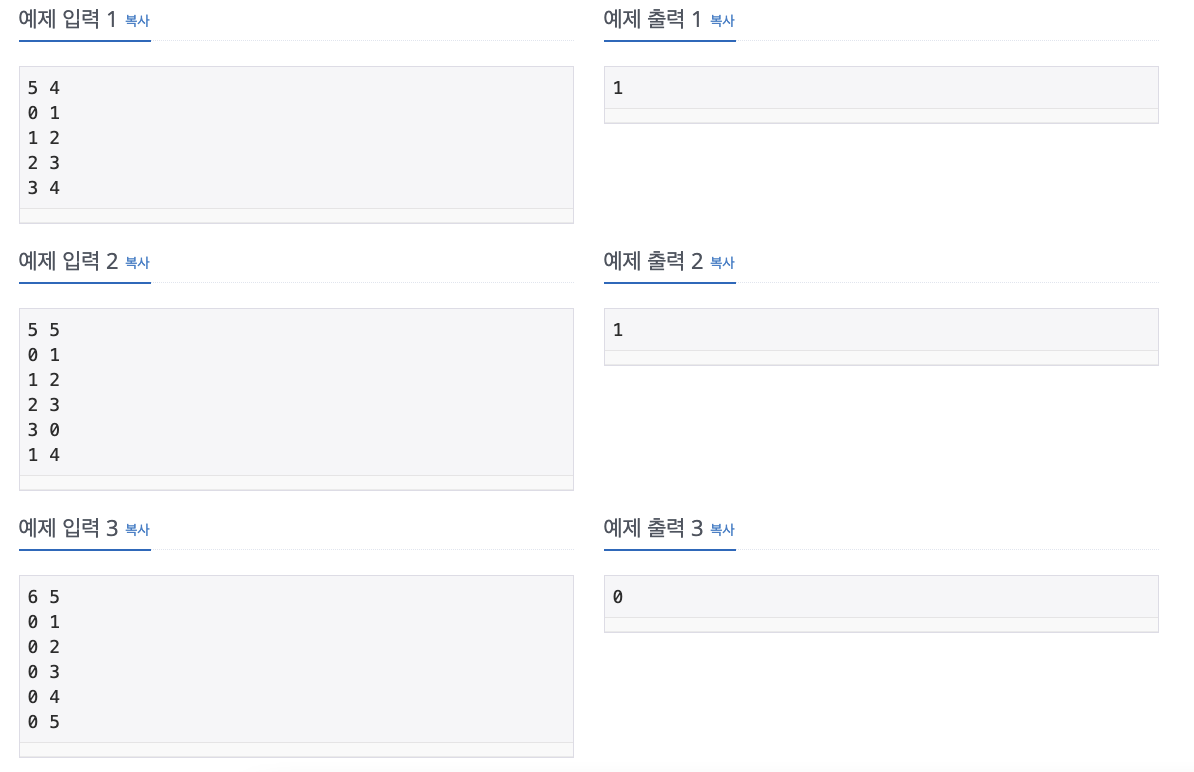
처음에 문제를 읽으면서 이게 뭔소리야.. 하면서 이해를 하지 못했다. A, B, C, D, E가 도대체 누구인지 명시되지 않았기 때문이다. 그래서 추측하기로는 총 N명의 참가자들이 있고 A, B, C, D, E와 같은 친구관계를 갖는 '아무나'가 존재하는지 찾으면 되는거 아닐까 이해했다.
즉 예제 입력 2를 그림으로 그려보면 왼쪽은 가능한 상황이고 오른쪽은 불가능한 상황이라고 볼 수 있다.
알고리즘
처음에 생각하기로는 Union-Find 문제일까? 근데 이거는 그런 유형과 맞지 않았다. 그다음으로 생각하기로 DFS/BFS였는데 BFS로는 이 문제를 풀기가 어렵다. 해보려고 시도는 했는데 차라리 DFS가 훨씬 낫기 때문에 최종적으로 DFS로 구현하였다.
DFS로 깊이가 4이상이 되면 성공이고, 4 미만이 나오면 존재하지 않는 경우다. 특히 DFS로 0부터 n-1까지 전부 조사를 해줘야한다. 왜냐면 어디서 시작할지에 따라서 깊이가 달라지기 때문. 예를 들어보면 아래와 같다.
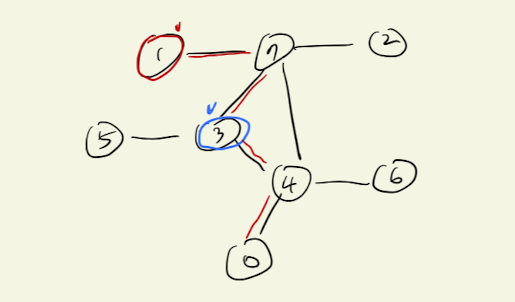
1에서 시작하면 깊이는 4가 나온다. 하지만 3부터 시작하면 깊이는 최대 3개뿐이 나오지 않는다.
Python
정답 코드
import sys
input = sys.stdin.readline
def dfs(v, depth):
global ans
visited[v] = True
if depth >= 4:
ans = True
return
if ans:
return
for node in graph[v]:
if not visited[node]:
dfs(node, depth + 1)
visited[node] = False
if __name__ == "__main__":
n, m = map(int, input().split())
graph = [[] for _ in range(n)]
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
visited = [False] * n
ans = False
for i in range(n):
dfs(i, 0)
visited[i] = False
if ans:
break
print(1 if ans else 0)
평소에 BFS로 주로 풀다보니 DFS로 구현하는게 미숙해졌다. DFS는 스택으로 구현하는 방식과 재귀로 구현하는 방식이 있는데 일반적으로는 재귀로 많이 구현하는 거 같다.
재귀함수로 깊이우선탐색을 진행하더라도 visited를 통해 중복은 제거해야한다. (visited가 없다면 이미 왔던 길을 되돌아가는것도 가능해지기 때문). 그리고 백트래킹처럼 되돌아오면 visited[node] = False로 초기화하는거 잊지말고.
✍️ 일반적으로는 DFS/BFS 둘 중 하나를 선택해서 탐색하면 되는 문제가 많은데 여기서는 DFS를 쓰는게 효과적이다. 내가 DFS 구현에 미숙하는 바람에 아쉽게 못풀게 되었다...ㅠㅠ (원리까지는 내가 맞았는데)
JavaScript
내 코드
const input = (() => {
let line = 0;
return () => stdin[line++];
})();
function dfs(n) {
if (visited[n] > 4) {
console.log(1);
process.exit();
}
for (let node of graph[n]) {
if (!visited[node]) {
visited[node] = visited[n] + 1;
dfs(node);
visited[node] = 0;
}
}
}
const [n, m] = input()
.split(" ")
.map((v) => parseInt(v));
const graph = Array.from(Array(n), () => Array(0));
let visited = Array(n).fill(0);
for (let i = 0; i < m; i++) {
const [a, b] = input()
.split(" ")
.map((v) => parseInt(v));
graph[a].push(b);
graph[b].push(a);
}
for (let i = 0; i < n; i++) {
visited[i] = 1;
dfs(i);
visited[i] = 0;
}
console.log(0);
✍️ 나는 체질상 DFS랑 안맞나봐..ㅋㅋ 풀긴 풀었는데 잔실수가 너무 많았고 그래서 시간도 오래걸림. 실제 코테라면 떨어졌다고 봐야지. 사실 DFS랑 DFS + 백트래킹(재귀)랑 별반 다르지 않다. 너무 어렵게 생각하지 말자....!!!
