개요
- 풀이 시간 : 30~40분
- 시간 제한 : 1초
- 메모리 제한 : 512 MB
- 기출 : backjoon
- 링크 : https://www.acmicpc.net/problem/15685
문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
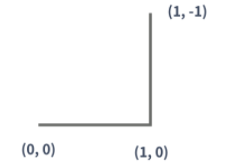
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.
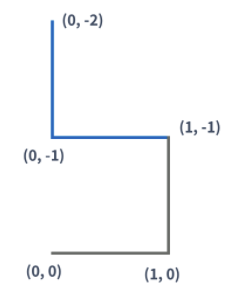
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
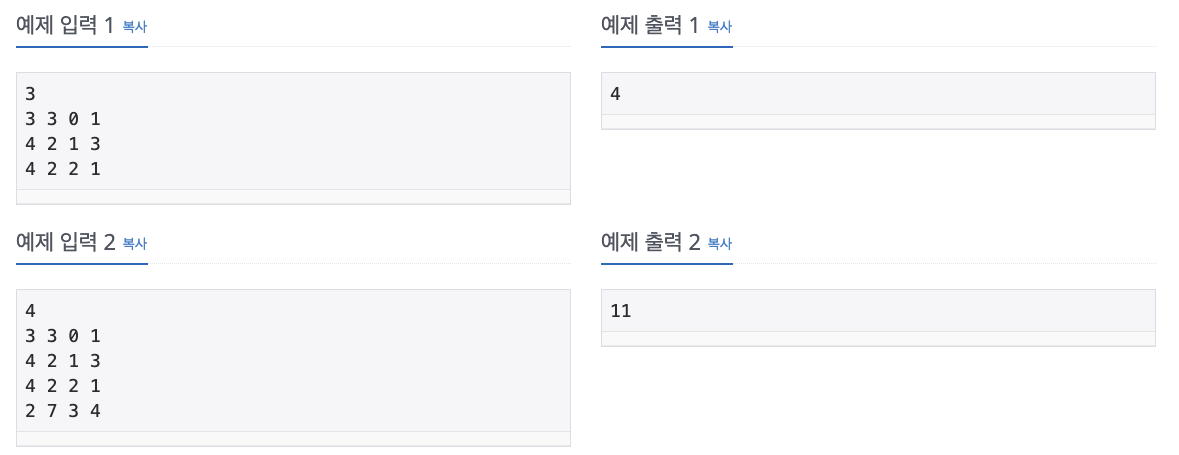
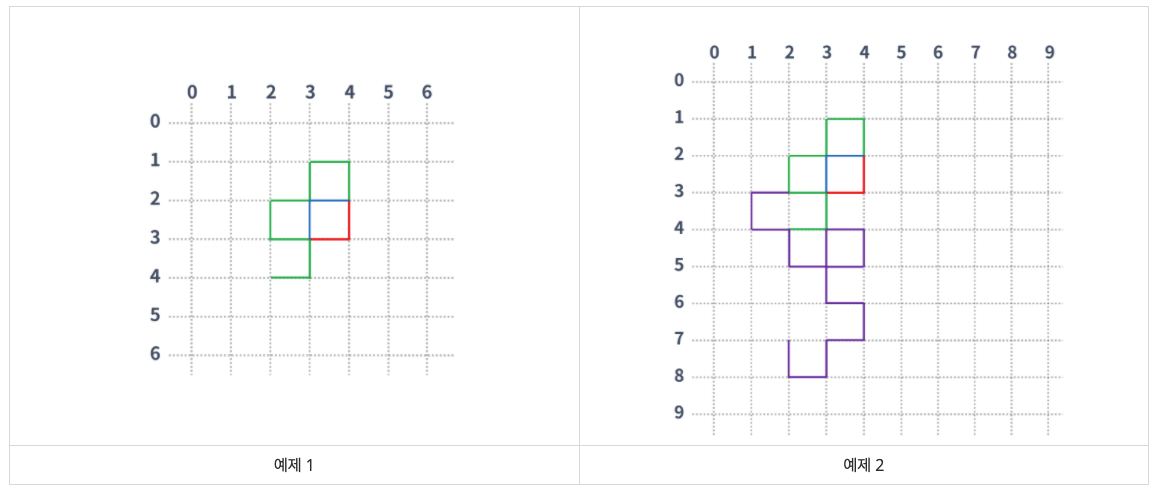
해결방법
문제 이해하기
문제를 일단 내가 처음에 조금 잘못이해한게 있었다. 문제에서는 "끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점" 이라고 했지만 나는 시작점에서 가장 먼 거리에 있는 점이라고 이해했다..ㅋㅋ 그래서 속으로 '와.. 그럼 매번 거리까지 계산해야하는 건가? 꽤 귀찮은데'라고 생각했었다.
아무튼 문제를 다시 읽고 이해는 했지만... 그런 해프닝이 있었다. 어쨌거나 이 문제는 그냥 단순히 시뮬레이션 해보고 규칙을 찾아서 구현하는 문제이다. 다만 이 규칙을 찾는데 어려운 편이다(나만 그래? 아님말고).
알고리즘
중요한건 좌표가 아니라 방향이다. 방향을 잘 보면 일정한 규칙성이 보인다.

이를 temp과 q 두개의 배열로 구현할 수 있다. temp은 이전세대 방향을 기록하고 있으며, q는 이전세대 방향에다가 1을 더하고 이를 뒤집어서 이동시킬 방향이 된다. (정답을 보고 있으면서도 이해하는데 조금 오래걸렸다...)

Python
정답 코드
import sys
input = sys.stdin.readline
# 동-북-서-남
dx = [0, -1, 0, 1]
dy = [1, 0, -1, 0]
if __name__ == "__main__":
n = int(input())
board = [[0] * 101 for _ in range(101)]
for _ in range(n):
# ⚠️ 좌표 주의! 문제에서는 가로가 x, 세로가 y
# 근데 일반적으로 나는 문제를 풀때 가로가 y, 세로가 x이므로 순서 전환 필요
y, x, d, g = map(int, input().split())
board[x][y] = 1
temp = [d]
q = [d] # 이동방향
for _ in range(g + 1): # 0~g세대
for k in q:
x += dx[k]
y += dy[k]
board[x][y] = 1
q = [(i + 1) % 4 for i in temp]
q.reverse()
temp = temp + q
result = 0
for i in range(100):
for j in range(100):
if (
board[i][j]
and board[i][j + 1]
and board[i + 1][j]
and board[i + 1][j + 1]
):
result += 1
print(result)
✍️ 오우... 생각보다 쉽지 않았던 문제였다.
