백준 1939번 - 중량제한(★★★ / ▲▲ / 2) : Python

개요

• 풀이 시간 : 30~40분
• 시간 제한 : 1초
• 메모리 제한 : 128 MB
• 기출 : backjoon
• 링크 : https://www.acmicpc.net/problem/1939

문제

N(2≤N≤10,000)개의 섬으로 이루어진 나라가 있다. 이들 중 몇 개의 섬 사이에는 다리가 설치되어 있어서 차들이 다닐 수 있다.

영식 중공업에서는 두 개의 섬에 공장을 세워 두고 물품을 생산하는 일을 하고 있다. 물품을 생산하다 보면 공장에서 다른 공장으로 생산 중이던 물품을 수송해야 할 일이 생기곤 한다. 그런데 각각의 다리마다 중량제한이 있기 때문에 무턱대고 물품을 옮길 순 없다. 만약 중량제한을 초과하는 양의 물품이 다리를 지나게 되면 다리가 무너지게 된다.

한 번의 이동에서 옮길 수 있는 물품들의 중량의 최댓값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N, M(1≤M≤100,000)이 주어진다. 다음 M개의 줄에는 다리에 대한 정보를 나타내는 세 정수 A, B(1≤A, B≤N), C(1≤C≤1,000,000,000)가 주어진다. 이는 A번 섬과 B번 섬 사이에 중량제한이 C인 다리가 존재한다는 의미이다. 서로 같은 두 도시 사이에 여러 개의 다리가 있을 수도 있으며, 모든 다리는 양방향이다. 마지막 줄에는 공장이 위치해 있는 섬의 번호를 나타내는 서로 다른 두 정수가 주어진다. 공장이 있는 두 섬을 연결하는 경로는 항상 존재하는 데이터만 입력으로 주어진다.

출력

첫째 줄에 답을 출력한다.

해결방법

문제 이해하기

난 이 문제를 섬과 다리가 있으므로 다익스트라 문제라고 생각했다. 하지만 곰곰히 생각해보면 최단 경로를 구하는 문제는 아니고 최대중량을 우선순위로 놓고 연결하겠끔하는 그런 문제였다. 완전 다익스트라를 아니더라도 조금 변형만 해서 우선순위 큐(힙)을 이용해 풀 수 있을거 같긴했다.

사실 다익스트라하고 신장 트리 중에 크루스칼 알고리즘하고 고민이 되긴했다. (나중에 문제 다 풀고 찾아보니 그렇게 풀어서 맞은 사람이 있긴 하더라)

알고리즘 - 우선순위 큐

이건 내가 푼 방식이다.

1. 일단 연결 리스트로 그래프 관계를 저장한다. 단, 서로 같은 두 도시 사이에 여러 개의 다리가 있을 수도 있다는 것에 주의.
2. 그렇게 저장한 다음 개별적으로 중량이 높은순서로 내림차순 정렬을 해준다.
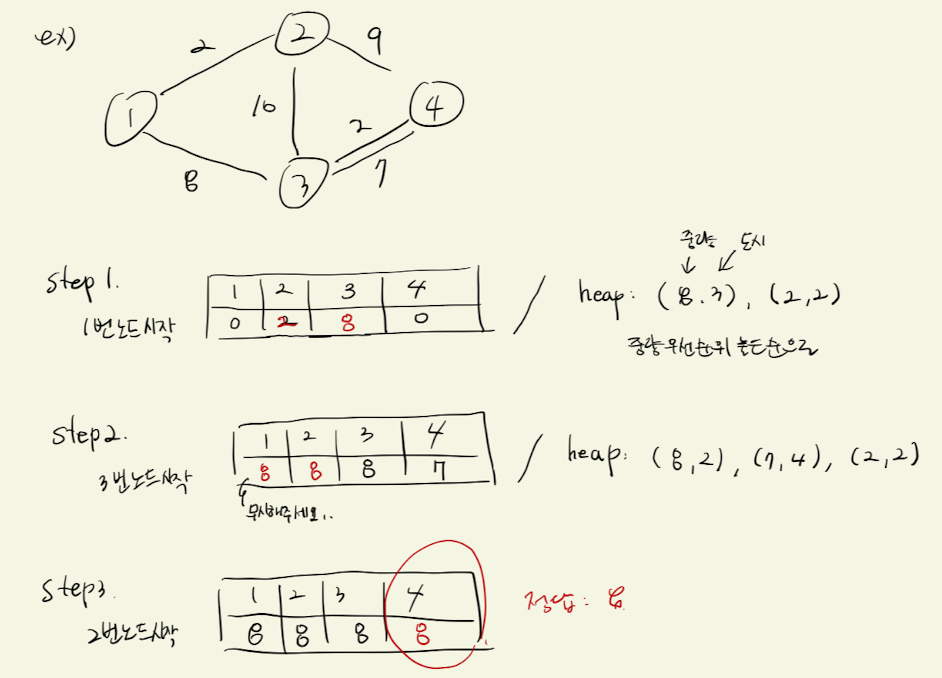
3. 이제 다익스트라를 시작한다. 그 이후 설명은 아래 그림으로 대체한다.

알고리즘 - (BFS + 이진탐색)

사실 백준에서는 이 문제를 그래프 탐색과 이진탐색으로 명시하고 있다. 코드를 한번 보니까 이렇게도 풀 수 있겠다 싶었다. 원리는 간단하다. 최소와 최대 중량을 정한다음 mid를 통해 중간값을 계산해서 BFS를 통해 목적지까지 도달할 수 있을까 살펴본다음에 mid 값을 이진탐색을 통해 조절해나가는 것이다.

쉽게말해 모의 트럭을 하나만들고 중량을 조절해서 실제 다리를 통과해서 되나 안되나 해보면서 값을 구하는 방법이다.

Python

내 코드

import heapq
import sys

input = sys.stdin.readline

def dijkstra(start, end):
    queue = []
    heapq.heappush(queue, (0, start))
    while queue:
        dist, now = heapq.heappop(queue)  # 최대힙
        dist = -1 * dist

        if now == end:
            print(dist)
            break

        if distance[now] > dist: # 이미 최대 중량인경우
            continue

        for i in graph[now]: # 정렬된 상태이므로 높은 중량부터 탐색이 됨.
            if dist == 0: # dist가 0인게 문제여...
                distance[i[1]] = i[0]
                heapq.heappush(queue, (-distance[i[1]], i[1]))
            # 기존에 저장된 값이 dist(이전 도시에서의 최대중량)와 현재 다리 최대 중량 보다 작다면...
            # 이렇게 한 이유는 다리가 중복 연결되어있는 가능성이 있기 때문
            elif distance[i[1]] < i[0] and distance[i[1]] < dist: 
                distance[i[1]] = min(dist, i[0]) # ✅ 이전도시 최대 중량과 현재 다리 최대 중량 중 작은 값을 저장
                heapq.heappush(queue, (-distance[i[1]], i[1]))



if __name__ == "__main__":
    n, m = map(int, input().split())
    graph = [[] for _ in range(n + 1)]
    for _ in range(m):
        a, b, c = map(int, input().split())
        graph[a].append((c, b))
        graph[b].append((c, a))

    for i in range(1, n + 1):
        graph[i].sort(reverse=True)

    distance = [0] * (n + 1)
    start, end = map(int, input().split())

    dijkstra(start, end)


"""
4 6
1 2 2
2 4 9
4 3 3
2 3 10
1 3 8
3 4 7
1 4
"""

이렇게 해서 풀 수는 있었지만 상당히 많은 시행착오를 거치면서 1시간 10분이나 걸렸다..ㄷㄷ (진짜 다리 중복만 없었어도 수월했을텐데)

추천 코드 - BFS + 이진탐색

from collections import deque
import sys

input = sys.stdin.readline


def bfs(mid):
    visited[start] = 1
    q = deque()
    q.append(start)

    while q:
        now = q.popleft()
        if now == end:
            return True
        for nx, nc in graph[now]:
            if visited[nx] == 0 and mid <= nc:
                q.append(nx)
                visited[nx] = 1

    return False


if __name__ == "__main__":
    n, m = map(int, input().split())
    graph = [[] for _ in range(n + 1)]
    for _ in range(m):
        a, b, c = map(int, input().split())
        graph[a].append((b, c))
        graph[b].append((a, c))

    for i in range(1, n + 1):
        graph[i].sort(reverse=True)

    start, end = map(int, input().split())
    low, high = 1, 1000000000
    while low <= high:
        visited = [0 for _ in range(n + 1)]
        mid = (low + high) // 2
        if bfs(mid): # 목적지까지 도달이 가능하다면 low를 올림
            low = mid + 1
        else: # 목적지까지 불가능하다면 high를 내림
            high = mid - 1

    print(high)

✍️ 이진 탐색을 생각 못했네...;; 뭐 풀이는 한가지만 있는건 아니니까. 이렇게도 생각해보고 저렇게도 생각해봐서 최선의 방법으로 빠르게 푸는게 중요한거지.

2차 풀이 - DFS + 이진탐색

import sys

sys.setrecursionlimit(1000000)
input = sys.stdin.readline

# start -> end까지 weight 무게로 통과가능한지
# DFS 재귀함수로 구현
def check(cur, weight):
    global end
    if cur == end:
        return True

    for node, bridgeW in graph[cur]:
        if bridgeW >= weight and not visited[node]:  # 중량이 넘지 않는다면
            visited[node] = True
            if check(node, weight):
                return True
            # visited[node] = False -> ✅ 이부분 때문에 자꾸 시간초과남

    return False


if __name__ == "__main__":
    n, m = map(int, input().split())
    graph = [[] for _ in range(n + 1)]
    for _ in range(m):
        a, b, c = map(int, input().split())
        graph[a].append((b, c))
        graph[b].append((a, c))

    start, end = map(int, input().split())

    left = 1
    right = 1000000000
    while left <= right:
        mid = (left + right) // 2
        visited = [False] * (n + 1)
        visited[start] = True

        if check(start, mid):
            left = mid + 1
        else:
            right = mid - 1

    print(right)

해당 문제를 복습하는 차원에서 다시한번 풀어봤다. DFS로 한번 구현해봤는데 왜 그런지 모르겠는데 저 위에 체크한 부분때문에 계속 시간초과가 나는거임... 정확성은 잘 나오는데... 근데 일반적인 DFS 구현은 위와 같이 하는게 맞지 않나? 물론 이 문제에서는 다시 False를 해줄 필요가 없긴한데 그렇다고 해도 이게 시간초과가 발생할 일인가 싶은데...? 🤔🤔

이 문제 해결해줄 사람 어디 없나~~??