백준 9252번 - LCS 2(★★★ / XX / 2) : Python/JavaScript

개요

• 풀이 시간 : 40분
• 시간 제한 : 1초
• 메모리 제한 : 256MB
• 기출 : 백준 9252번 문제
• 링크 : https://www.acmicpc.net/problem/9252

문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.

LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.

해결방법

문제 이해하기

이 문제를 처음에 잘못 이해한게 만약 AC와 CAE가 있을때 AC도 가능할줄 알았다. 근데... 순서도 같아야 하는 모양이다. 예를들어 CA와 CEA가 있으면 CA가 가능한것처럼 말이다. 아 그리고 첫번째 문자열의 길이와 두번째 문자열의 길이는 다를 수 있다는 것에 주의하자.

처음에 이문제를 딱 보고 이것이 코딩테스트다에서 본 편집 거리문제가 생각났다. 그니까 편집거리 문제처럼 2차원배열로 풀면 가능하지 않을까? 생각은 했는데... 규칙을 어떻게 세워야 할지 감이 안잡혀서 실패...

알고리즘

0. 2차원 dp를 활용한다.
1. 행은 첫번째 문자열, 열은 두번째 문자열에 대한 정보를 나타낸다.
2. dp[row][col]은 첫번째 문자열 row의 길이, 두번째 문자열 col의 길이에 해당하는 문자열로 만들 수 있는 공통부분 수열이다.
3. 첫번째 문자열과 두번째 문자열 길이를 이용해 2차원 for문을 돈다.
4. 첫번째 문자열의 i번째와 두번째 문자열의 j번째 문자를 비교한다
   4.1 일치한다면 dp[i][j] = dp[i-1][j-1] + 문자
   4.2 일치하지 않는다면 dp[i][j] = dp[i-1][j]와 dp[i][j-1]에서 길이가 긴 것을 대입한다.

예시

초기 2차원 배열

중간까지 진행한 2차원 배열 결과

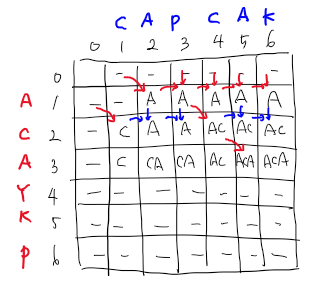
값이 일치한다면 dp[i][j] = dp[i-1][j-1] + 문자,
일치하지 않는다면 dp[i][j] = dp[i-1][j]와 dp[i][j-1]에서 길이가 긴 것

Python

정답 코드

string_1 = list(input())
string_2 = list(input())

dp = [[""] * (len(string_2) + 1) for _ in range(len(string_1) + 1)]

for i in range(1, len(string_1) + 1):
    for j in range(1, len(string_2) + 1):
        if string_1[i - 1] == string_2[j - 1]:
            dp[i][j] = dp[i - 1][j - 1] + string_1[i - 1]
        else:
            if len(dp[i - 1][j]) >= len(dp[i][j - 1]):
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = dp[i][j - 1]

        print(dp)

if len(dp[-1][-1]) == 0:
    print(0)
else:
    print(len(dp[-1][-1]))
    print(dp[-1][-1])

JavaScript

정답 코드

const a = input();
const b = input();
const aLength = a.length;
const bLength = b.length;

const dp = Array.from(Array(aLength + 1), () => Array(bLength + 1).fill(""));
for (let i = 1; i < aLength + 1; i++) {
  for (let j = 1; j < bLength + 1; j++) {
    if (a[i - 1] === b[j - 1]) {
      dp[i][j] = dp[i - 1][j - 1] + b[j - 1];
    } else {
      if (dp[i][j - 1].length > dp[i - 1][j].length) {
        dp[i][j] = dp[i][j - 1];
      } else {
        dp[i][j] = dp[i - 1][j];
      }
    }
  }
}

if (dp[aLength][bLength].length == 0) {
  console.log(0);
} else {
  console.log(dp[aLength][bLength].length);
  console.log(dp[aLength][bLength]);
}

사실 규칙만 찾으면 쉬운 문제다. 2번째 시도는 풀 수 있을거라고 생각했지만 실패. 패착의 원인은 바로 표에다가 문자열이 아닌 숫자를 넣었기 때문... 또한 규칙을 제대로 찾지 못했다. 잘 생각만 하면 될텐데 너무 아쉽네...

• 문자가 일치하면 대각선 + 문자
• 문자가 일치하지 않으면 위쪽과 왼쪽에서 길이가 더 긴 문자열