개요
- 풀이 시간 : 30~40분
- 시간 제한 : -
- 메모리 제한 : -
- 기출 : 월간 코드 챌린지 시즌 2
- 링크 : https://programmers.co.kr/learn/courses/30/lessons/76503
문제
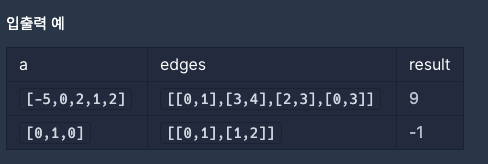
각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다.
- 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한쪽은 1 감소시킵니다.
하지만, 모든 트리가 위의 행동을 통하여 모든 점들의 가중치를 0으로 만들 수 있는 것은 아닙니다. 당신은 주어진 트리에 대해서 해당 사항이 가능한지 판별하고, 만약 가능하다면 최소한의 행동을 통하여 모든 점들의 가중치를 0으로 만들고자 합니다.
트리의 각 점의 가중치를 의미하는 1차원 정수 배열 a와 트리의 간선 정보를 의미하는 edges가 매개변수로 주어집니다. 주어진 행동을 통해 트리의 모든 점들의 가중치를 0으로 만드는 것이 불가능하다면 -1을, 가능하다면 최소 몇 번만에 가능한지를 찾아 return 하도록 solution 함수를 완성해주세요. (만약 처음부터 트리의 모든 정점의 가중치가 0이라면, 0을 return 해야 합니다.)
입력 형식
- a의 길이는 2 이상 300,000 이하입니다.
- a의 모든 수는 각각 -1,000,000 이상 1,000,000 이하입니다.
- a[i]는 i번 정점의 가중치를 의미합니다.
- edges의 행의 개수는 (a의 길이 - 1)입니다.
- edges의 각 행은 [u, v] 2개의 정수로 이루어져 있으며, 이는 u번 정점과 v번 정점이 간선으로 연결되어 있음을 의미합니다.
- edges가 나타내는 그래프는 항상 트리로 주어집니다.
해결방법
문제 이해하기
월간 코드 챌린지 시즌 2 문제이다. 대략 2주전 프로그래머스에서 진행했던 이벤트성 코딩테스트이며 나도 그때 참석해서 문제를 풀었었다. 해당 문제는 4문제 중에서 3번 문제였으며 아쉽게도 그때는 50점의 점수밖에 획득하지 못했었다... 그래서 이번에 재도전하는 것이다.
문제를 이해해보면 간단하다. 각 노드마다 가중치 값이 있으며 이런 가중치 값을 연결된 노드 사이로 옮길 수 있다. 이렇게 해서 최소 동작을 통해 모든 가중치를 0으로 만드는 게 문제 핵심이다.
알고리즘 - 트리 순회
일단 지금 생각난 방법은 트리 중위 순회를 사용해보는건 어떨까? 즉, 왼쪽 서브 트리 가중치 합산하고, 오른쪽 서브 트리 가중치 합산하고... 마지막으로 중앙 노드 가중치와 합산해서 올라가는 형태를 말한다. 근데 곰곰히 생각해보면 이런생각이 들었다. '큰 가중치가 있는 노드는 되도록이면 옮기지 말아야 하는거 아닌가?' 과연 그 말이 사실일까? 검증해봤다.
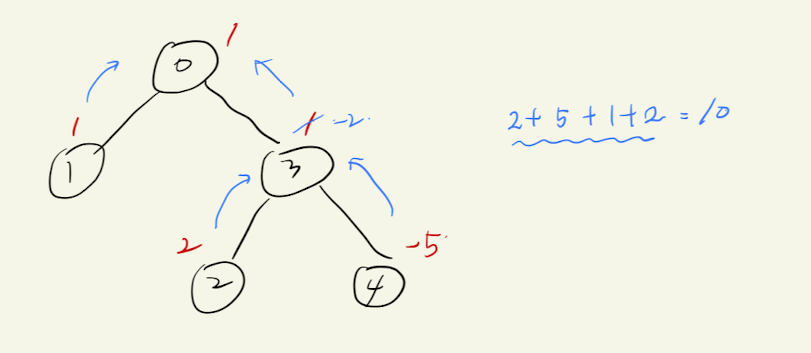
만약 서브 트리 노드에서의 가중치가 더 크다면 어떨까? 이때 트리 순회를 해보면 결과가 10이 나왔다. 반대로 -5는 가만히 있고 나머지가 움직인다면 어떨까? 1 + 2 + 3 + 2 + 2 = 10.. 어쨌거나 결과는 똑같은 것을 확인할 수 있다. 따라서 내가 생각한 방식대로 해도 큰 문제를 없을거 같았다.
Python
내 코드
import sys
sys.setrecursionlimit(1000000)
result = 0
def treeInorderTraversal(num, count, a, graph, visited):
global result
visited[num] = True
for node in graph[num]:
if not visited[node]:
a[num] += treeInorderTraversal(node, count, a, graph, visited)
result += abs(a[num]) # ✅ 절댓값 주의할 것!!
return count + a[num]
def solution(a, edges):
sumWeight = 0
isZeroTrue = True
for weight in a:
sumWeight += weight
if a != 0:
isZeroTrue = False
if sumWeight != 0:
return -1
elif isZeroTrue:
return 0
else:
# 트리 탐색을 수행? (중위탐색)
graph = [[] for _ in range(len(a))]
visited = [False] * len(a)
for edge in edges:
x, y = edge
graph[x].append(y)
graph[y].append(x)
treeInorderTraversal(0, 0, a, graph, visited)
return result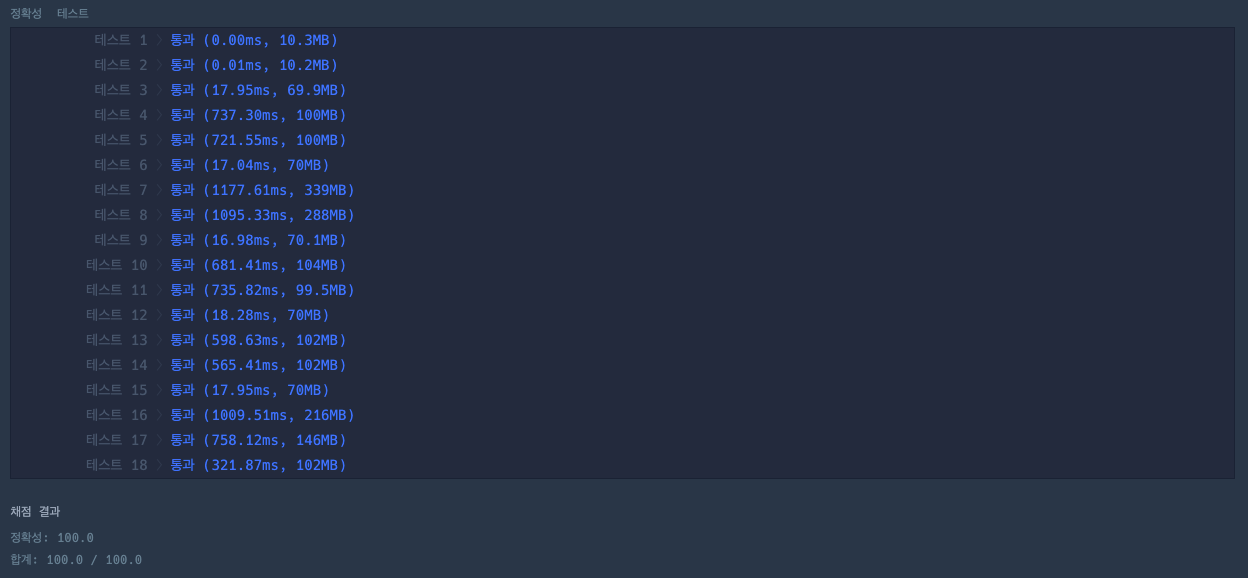
✍️ 프로그래머스 다른 코드 풀이도 이와 크게 다르지 않았다. (굿~)
