https://www.yes24.com/Product/Goods/92867606
양자컴퓨터?
양자역학 특유의 물리 상태를 적극적으로 이용해 고속 계산을 구현하는 컴퓨터
동작 흐름
- 양자비트 초기화
- 양자 연산
- 계산 결과 읽기
양자비트
블로구 구에서 화살표의 상태를 바탕으로 0과 1이 측정될 확률을 알 수 있음.
양자 게이트
고전컴퓨터는 논리 게이트를 다수 조합해서 계산한다.
논리 게이트: 비트에 작용하는 연상
단일 양자비트 연산
- X: 양자 NOT 게이트, 비트 플립 (|0⟩를 |1⟩로, |1⟩를 |0⟩로).
- H: 하다마드 게이트, 양자 상태를 중첩 상태로 변환 (|0⟩와 |1⟩의 중첩 상태를 만듦).
- Y: 파울리 Y 게이트, 양자 상태의 위상을 변화시키며 비트도 플립.
- S: 위상 게이트, 특정 상태의 위상을 π/2만큼 증가.
- Z: 파울리 Z 게이트, 상태 |1⟩의 위상을 π만큼((|-1⟩) 변화 (|0⟩는 변화 없음).
- T: T 게이트, 위상을 π/4만큼 조절.
다중 양자비트 연산
- CNOT: 제어된 NOT 게이트, 첫 번째 비트(제어 비트)가 |1⟩일 때 두 번째 비트(타겟 비트)를 플립.
- CZ: 제어된 Z 게이트, 제어 비트가 |1⟩일 때 타겟 비트에 Z 게이트 적용.
- Toffoli: 제어된 제어 NOT 게이트, 두 제어 비트 모두 |1⟩일 때 세 번째 비트를 플립.
- SWAP: 두 양자비트의 상태를 서로 교환.
- CS: 제어된 S 게이트, 제어 비트가 |1⟩일 때 타겟 비트에 S 게이트 적용.
- Fredkin: 제어된 SWAP 게이트, 제어 비트가 |1⟩일 때 두 타겟 비트의 위치를 교환.
양자 게이트의 연산은 블로후 구에서 화살표의 회전 연산으로 이해하면 됨
양자 회로
양자 게이트를 조합해서 회로를 만든다.
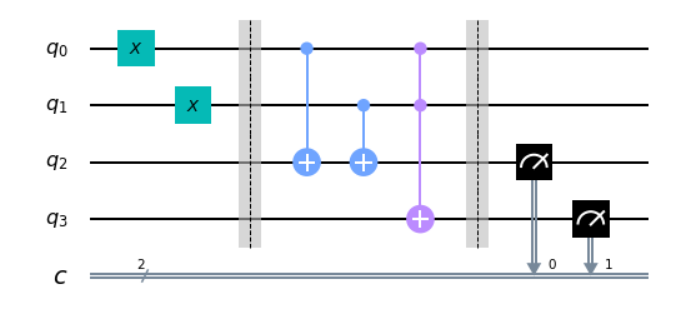
- 시간은 왼쪽에서 오른쪽으로 진행됨
- 양자비트 처음 상태(초기 상태)는 0으로 하기로 약속되어 있음.
- 초기 상태는 계산의 입력이 아니다! 계산의 입력은 양자 게이트로 조합으로 나타낸다.
- 계산의 출력(계산 결과)는 양자비트의 상태 측정 결과
- 입력 부분에 두는 양자 게이트의 조합으로 계산의 입력을 나타냄.
SWAP 회로
2개의 양자비트의 상태를 교환하는 회로
CNOT 게이트 3개를 조합해서 구현 가능
덧셈 회로
근데 이러면 고전 컴퓨터와 똑같잖아?
그래서 양자 회로 입력에 X가 아닌 H로 중첩 상태를 입력할 수 있음.
그럼 입력이 중첩되니까 동시에 병렬 계산이 가능하다.
근데 문제는 이 경우 결과가 랜덤이다.
가역 계산
출력 상태로부터 입력 상태를 추측할 수 있는 계산
고전 계산에서 NOT 게이트가 해당
입력과 출력의 수가 다른 고전 계산에서는 불가역 계산이다.
가역 계산이 되려면 NOT 게이트처럼 입력과 출력의 수가 같아야 한다.
이론적으로 가역 계산에는 에너지가 필요 없다.(란다우어의 원리)
측정
"측정 전부터 양자비트의 상태는 사실 확정되어 있지만 우리가 모르는 것뿐이다" -> 이게 절대 아님!
정말로 측정이라는 행위를 하는 순간에 양자비트의 성질이 변화하는 것!
얽힘
H와 CNOT으로 양자얽힘을 만들 수 있음.
양자 텔레포테이션
양자 역학의 기본 원리를 이용하여 어떤 양자 상태를 한 위치에서 다른 위치로 "전송", 엄밀히 따지면 '복사'가 아닌 '재생성'이다.
간단히 요약하면 먼저 얽힘 상태로 비트를 나눠 가진다.
그 다음 전송하려면 중첩 상태의 비트를 보내는 쪽에서 연산한다.
그 다음 고전 통신으로 측정 결과를 알려준다.
받는 쪽에서 연산을 걸어 최초 중첩(프사이) 상태를 재현한다.
고전 통신이 필요하므로 빛의 속도를 넘어서 전송되지 않는다.
그리고 보내는 쪽의 정보가 파괴(측정)하고 받는 쪽에서 재현하는 셈이기 때문에 정보를 복제할 수 없다.
from qiskit import QuantumCircuit, execute, Aer
from qiskit import QuantumCircuit, execute, Aer, ClassicalRegister
# 양자 회로 설정
qc = QuantumCircuit(3, 3)
# Alice가 전송하고자 하는 중첩 상태 준비
qc.h(0) # 큐비트 0에 하다마드 게이트 적용하여 중첩 상태 생성
qc.barrier()
# 얽힘 상태 생성 (큐비트 1과 2)
qc.h(1)
qc.cx(1, 2)
qc.barrier()
# Alice가 큐비트 0과 큐비트 1에 벨 상태 측정을 수행
qc.cx(0, 1)
qc.h(0)
qc.measure([0, 1], [0, 1]) # 결과를 고전 비트 0과 1에 저장
qc.barrier()
# Bob의 유니터리 연산을 위한 조건문 추가
qc.x(2).c_if(
1, 1
) # 조건부 X 게이트: 고전 비트 1의 값이 1일 때 큐비트 2에 X 게이트 적용
qc.z(2).c_if(
0, 1
) # 조건부 Z 게이트: 고전 비트 0의 값이 1일 때 큐비트 2에 Z 게이트 적용
# 11 케이스는 자동적으로 X 다음에 Z가 적용
# Bob의 큐비트 상태 확인을 위한 측정 (선택 사항)
# qc.measure(2, 2)
# 시뮬레이터 설정 및 회로 실행
simulator = Aer.get_backend("qasm_simulator")
job = execute(qc, simulator, shots=1024)
results = job.result()
# 결과 출력
counts = results.get_counts()
print("측정 결과 카운트: ", counts)
# 측정 결과 카운트: {'001': 246, '011': 250, '010': 275, '000': 253}qasm_simulator는 측정하지 않으면 기본값0으로 간주하고 출력한다.
오른쪽부터 0번 큐비트, 제일 왼쪽이 2번(최종 전송된 큐비트)
전송 큐비트 0.99|1> 인 경우
from qiskit import QuantumCircuit, execute, Aer
import math
# 각도 설정: |1>의 확률을 약 99%로 설정
theta = 2 * math.acos(math.sqrt(0.01))
# 양자 회로 설정
qc = QuantumCircuit(3, 3)
# Alice가 전송하고자 하는 중첩 상태 준비
qc.ry(theta, 0) # 큐비트 0에 Ry 게이트를 적용하여 |1>의 확률을 99%로 만듦
qc.barrier()
# 얽힘 상태 생성 (큐비트 1과 2)
qc.h(1)
qc.cx(1, 2)
qc.barrier()
# Alice가 큐비트 0과 큐비트 1에 벨 상태 측정을 수행
qc.cx(0, 1)
qc.h(0)
qc.measure([0, 1], [0, 1]) # 결과를 고전 비트 0과 1에 저장
qc.barrier()
# Bob의 유니터리 연산을 위한 조건문 추가
qc.x(2).c_if(
1, 1
) # 조건부 X 게이트: 고전 비트 1의 값이 1일 때 큐비트 2에 X 게이트 적용
qc.z(2).c_if(
0, 1
) # 조건부 Z 게이트: 고전 비트 0의 값이 1일 때 큐비트 2에 Z 게이트 적용
# Bob의 큐비트 상태 확인을 위한 측정 (선택 사항)
qc.measure(2, 2)
# 시뮬레이터 설정 및 회로 실행
simulator = Aer.get_backend("qasm_simulator")
job = execute(qc, simulator, shots=1024)
results = job.result()
# 결과 출력
counts = results.get_counts()
print("측정 결과 카운트: ", counts)
결과가 다음과 같이 나왔다.
측정 결과 카운트: {'001': 2, '110': 232, '100': 262, '011': 3, '111': 255, '010': 2, '000': 3, '101': 265}2번 큐비트는 1 확률이 높다. 중첩 상태의 최초 큐비트가 제대로 전송됐다고 볼 수 있다.

양자얽힘
quantum entanglement
H, CX 게이트로 얽힘을 만들 수 있음.


양자 알고리즘
계산 결과의 정답에 해당하는 상태의 확률진폭만 잘 증가시키고, 다른 틀립 답에 해당하는 상태의 확률진폭을 없앰으로써 확률진폭을 저하시키도록 양자 회로를 설계하는 것
그로버 알고리즘
탐색 문제를 푸는 알고리즘
탐색 문제: 특정 조건을 만족하는 답을 찾아내는 문제
쇼어 알고리즘
1994 피터 쇼어 발표
실용성 있는 최초의 양자 알고리즘
소인수분해 고속화라는 현대 암호시스템의 기반을 흔드는 알고리즘
RSA 2048 해독하려면 천만~1억 큐비트가 필요하므로 단기간 실현은 안 됨.
양자 컴퓨터 작동 원리
양자 회로도 -> 입력 펄스열 -> QPU 동작
초전도 큐비트의 경우 마이크로파 펄스를 보내서 비트를 제어
펄스는 매우 정밀하게 제어되어야 하며, 큐비트에 공명하는 특정 주파수에서 전달.
입력 펄스열은 양자 회로도에 정의된 양자 게이트를 큐비트에 물리적으로 구현하기 위해 사용됨.
QPU: 양자 프로세싱 유닛, 실제 큐비트가 포함된 하드웨어. QPU 내에서는 큐비트들이 양자 얽힘 및 중첩 같은 양자역학적 특성을 이용하여 데이터를 처리하고, 최종적으로 양자 측정을 통해 결과를 얻음.
양자 어닐링
조합최적화 문제에 특화된 기법
'양자 어닐러'를 통해 해결
양자 어닐링을 실행하기 위해서는 문제를 이징 모델로 변환해야 함.
이징 모델의 스핀은 양자비트 자체가 된다.
양자 회로 모델이 만능 양자 계산이라면,
양자 어닐링은 특화된 전용기
양자 어닐링이 진짜 양자 컴퓨팅에 대한 논란은 있음.
양자비트 만드는 법
고전컴퓨터 CPU는 반도체 기반의 '트랜지스터'로 비트를 구현한다.
초창기에는 릴레이, 진공관, 파라메트론 등의 소자를 이용한 계산기가 있었음.
- 초천도 회로
- 이온 트랩 / 냉각 원자
- 반도체 양자점
- 다이아몬드 NV센터
- 광자적 양자 계산
- 토폴로지컬
현재 주류로 기대받고 있는 건 IBM 주도의 초전도 회로에 의한 양자비트 구현 방식
초전도 회로
극저온으로 냉각된 특정 금속은 전기 저항이 0인 초전도 상태가 됨.
이 상태는 양자성을 강하게 나타내므로 양자비트를 구현할 수 있음.
양자성이 강하게 나타난다는 말은 측정할 때까지는 파동의 성질을 가진 중첩 상태를 구현할 수 있다는 것을 의미.
즉, 초전도 회로에 의해 0과 1의 중첩 상태를 구현할 수 있음.
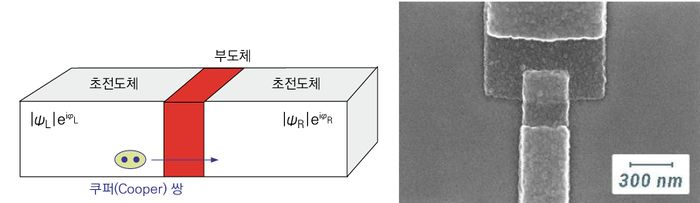
조셉슨 접합
초전도 회로에서는 조셉슨 접합이라는 구조로 양자 비트를 구현한다.
이건 초전도-절연층-초전도의 간단한 샌드위치 구조임.
절연층은 원래 전기가 통하지 않는다.
하지만 아주 얇은 1nm 정도 절연층에서는 전자의 파동성에 의해 절연층을 빠져나갈 수 있다.(=전류가 흐른다.)
이런 현상을 터널 효과라고 함.
이 현상을 통해 양자비트에 필요한 비선형성을 획득하여, 초전도 양자비트를 구현하는 것.
초전도 회로 구현 방법
- 트랜스몬
- 자속 양자비트
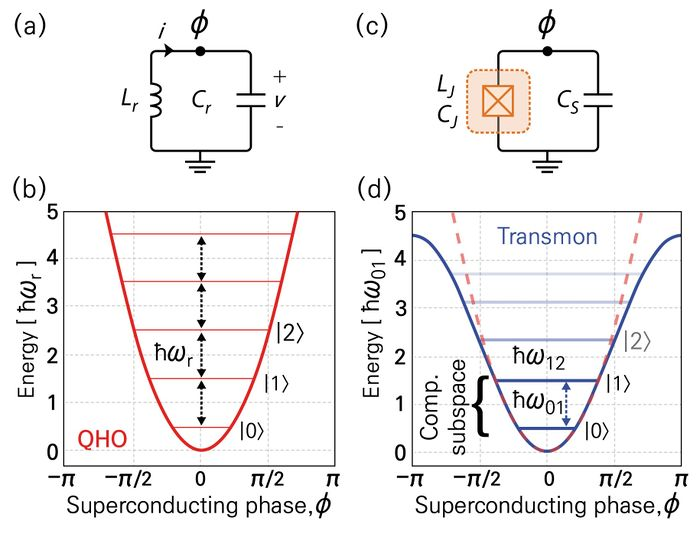
트랜스몬
조셉슨 접합의 비선형성에 의해 에너지 준위 간격을 불균일하게 해서 2준위계를 준비해 양자비트로 함.
양자 회로 모델의 양자컴퓨터 구현에 이용.
노이즈에 강함. 코히어런스 시간이 길다.
자속 양자비트
조셉슨 접합을 포함한 초전도 회로의 루프 구조를 만들어 루프 내 전류의 우회전과 좌회전으로 0과 1의 중첩 상태를 구현.
현재는 양자 어닐링에 사용회고 있음.
코히어런스 시간이 떨어지지만, 많은 양자 비트 구현 가능.
양자의 상태
순수상태
양자비트 상태 그 자체
혼합상태
양자 역학과 관련없는 고전적인 확률
양자비트의 확률진폭은 양자적인 확률,
동전의 앞뒤가 나올 확률을 고전적인 확률
고전적인 확률에는 간섭 효과가 없다.
고전적인 확률을 가진 확률비트를 양자 계산에 이용하면 간섭 효과가 없기 때문에 올바른 양자 계산을 할 수 없다.
즉, 양자적인 확률이라는 특징을 이용하기 위해서는 순수상태를 매우 높은 비율로 가진 양자비트가 필요하며 양자비트를 흉내낸 것은 양자 계산을 할 수 없다.
이미 결정된 양자비트에 H를 걸면 중첩이 된다. 이건 처음 상태와 무관하게 무조건 중첩이 되는 거고 간섭 효과가 없는 거다.
근데 중첩 상태에 H를 걸면 0으로 된다. 이건 간섭효과가 있는 거다.
간섭 효과
간섭 효과는 양자 상태의 중첩으로 인해 발생합니다. 양자 시스템에서는 한 큐비트가 동시에 여러 상태를 가질 수 있는 중첩 상태에 있을 수 있습니다. 이 큐비트들이 서로 다른 양자 게이트를 통과하면서 다양한 경로를 경험하게 되고, 이 경로들이 만나게 되면 각 경로의 파동 함수가 서로 간섭을 일으키게 됩니다.
간섭은 계산 과정에서 원하지 않는 상태를 제거하고, 원하는 상태의 확률을 증가시키는 데 사용됩니다.
디코히어런스
순수상태가 혼합상태로 변화해 버리는 것
