양자 컴퓨팅 개론

ClassBinu·2024년 4월 5일

양자 컴퓨팅

목록 보기

1/17

양자

양자역학에서 "양자"는 에너지가 불연속적인 최소 단위로 존재한다는 개념을 나타냅니다. 이는 에너지가 연속적인 스펙트럼으로 분포하는 대신, 특정한 "양"으로만 교환될 수 있다는 아이디어를 기반으로 합니다. 양자역학의 이러한 기본적인 전제는 물질과 에너지가 입자와 파동의 성질을 모두 갖는다는 파동-입자 이중성과 긴밀하게 연결되어 있습니다.

"양자"라는 용어는 또한 더 구체적으로, 개별적인 입자들(예: 전자, 광자, 쿼크 등)을 나타내는 데도 사용됩니다. 이 입자들은 양자 역학의 법칙에 따라 행동하며, 그들의 위치, 속도, 에너지 상태 등은 확률적으로만 예측할 수 있습니다. 양자역학은 이러한 입자들의 행동을 설명하고 예측하기 위한 이론적 틀을 제공합니다.

하이젠베르크 불확정성 원리

양자 시스템의 특정 쌍의 물리량(예: 위치와 운동량)을 동시에 임의의 정밀도로 알 수 없다는 것을 의미합니다. 이러한 원리는 양자역학이 기존의 고전 물리학과 근본적으로 다른 방식으로 자연을 이해하는 데 도움을 줍니다.

양자 현상

중첩

측정되기 전까지 양자가 여러 상태 조합을 동시에 가질 수 있음.
측정이 이루어지면 시스템은 특정 상태로 '붕괴'

얽힘

두 개 이상의 입자가 양자 얽힘 상태에 있을 때,
한 입자의 상태를 측정하면 즉각적으로 다른 입자의 상태도 결정
이 현상은 입자들이 물리적으로 떨어져 있어도 발생
비국소성(nonlocality)의 예

nonlocality란?
고전 물리학의 국소성 원칙과 대비
고전 물리학에서는 물체들이 서로 직접적으로 영향을 주고 받으려면 물리적으로 연결되어 있어야 함. 즉, 상호 작용은 빛의 속도 내에서 국소적인 범위에서만 발생
하지만 양자 비국소성에서는 물리적 거리에 관계 없이 상호 작용이 즉각적으로 발생

관측

파동-입자 이중성
물질과 빛은 동시에 파동과 입자의 성질을 가질 수 있음.
그리고 관측이 물질의 상태에 영향을 미친다.

이중 슬릿 실험에서 광자를 발사할 때,
관측하지 않으면 간섭 패턴(파동)이 나타나지만
관측하면 간섭 패턴이 사라지고 광자가 두 슬릿 중 하나를 통과한 것처럼(입자) 두 줄이 찍힘

큐비트

bit: binary digit (0 or 1)
qubit: quantum bit (0 and 1)

양자 상태는 2가지만 존재하는 게 아님. 여러 상태가 중첩될 수 있음.
근데 어려우니까 우선 2개 상태만 가정함.

양자 수식

배경 지식

프사이: Ψ, ψ, 슈뢰딩거 파동방정식의 해인 '파동함수' 의미
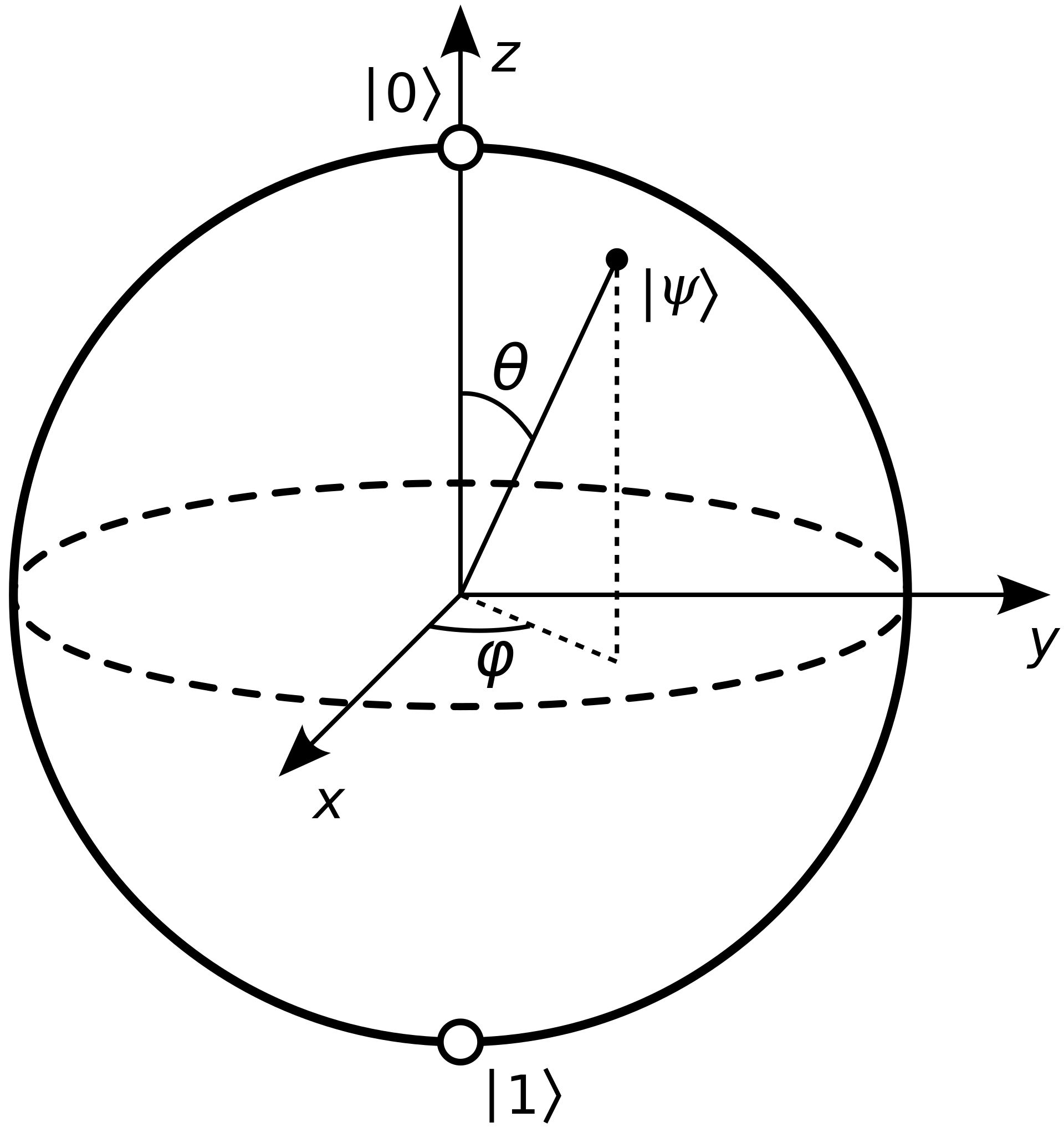
켓(ket) 표기법: ∣0⟩, 이거 자체가 off 상태의 큐비트를 나타냄(1이면 on 상태)
블로흐 구면: 2단계 양자계를 기하학적으로 나타낸 것. 큐비트 상태를 쉽게(직관적으로) 나타낼 수 있음.
확률 진폭: 양자 상태를 기술하는 복소수(물리적 의미가 아님)
확률: 양자역학에서 확률 진폭의 제곱의 절댓값

양자 상태를 나타내는 파동함수(프사이)는 여러 상태의 중첩으로 표현
이를 선형 조합으로 나타낼 수 있음.

예를 들어 큐비트가 0, 1의 중첩이라면 이렇게 표현

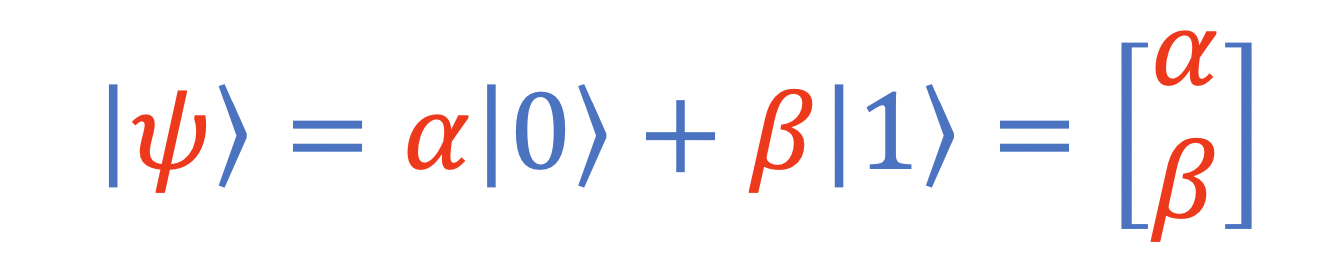
(벡터의 행렬로 표현 가능)

알파와 베타는 각각 0, 1에 대한 확률 진폭임.
확률 진폭을 제곱하면 확률이 됨.

알파 제곱은 시스템이 상태 0에 있을 확률,
베타 제곱은 시스템이 상태 1에 있을 확률

모든 가능성의 합은 1이어야 함.
그래서 이 수식이 성립함.

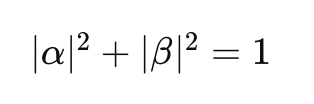
이건 블로흐 구면으로 나타낼 수 있음.
북극점은 0, 남극점은 1을 나타내며, 구의 다른 모든 점을 0과 1의 중첩 상태

프사이 제곱은 특정 위치에 입자가 발견될 확률 밀도
즉, 프사이 위치를 보면 해당 양자가 0인 확률과 1인 확률을 구할 수 있음.

양자 회로도

Quantum Circuit Diagram

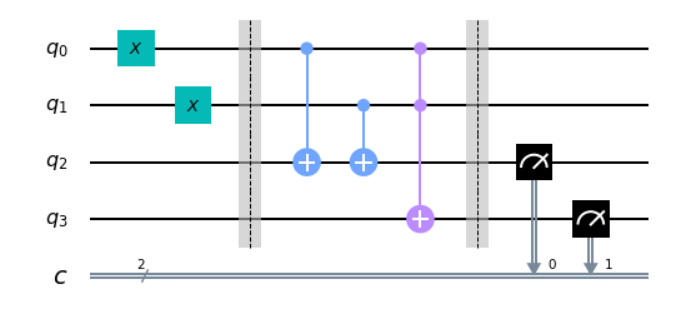
가로선은 각각의 큐비트
왼쪽에서 오른쪽으로 시간이 흐름
H: 하다마드 게이트
X, Y, Z: 폴리 게이트
CNOT 케이트
동그란 점: 제어 큐비트
점과 연결된 선: 제어 큐비트의 제어를 받는 대상 큐비트
미터기 같은 심볼: 상태 측정 시점, 측정 결과는 고전 정보(0 or 1)로 변환

https://wiki.quist.or.kr/index.php/%EC%96%91%EC%9E%90%EC%BB%B4%ED%93%A8%ED%8C%85_(Quantum_Computing)

QASM

Quantum Assembly Language
양자 컴퓨터 프로그래밍을 위한 저수준 어셈블리 언어

OPENQASM 3;
include 'customgates.inc';

bit[4] c;
qubit[4] q;

h q[0];
cx q[0], q[1];

c[0] = measure q[0];
c[1] = measure q[1];
c[2] = measure q[2];
c[3] = measure q[3];

양자 게이트

큐비트의 상태를 변환하는 기본적인 연산 단위

고전 컴퓨터에서는 AND, OR, NOT 같은 게이트로 연산한다.
양자 컴퓨터에서는 양자 게이트로 연산을 한다.

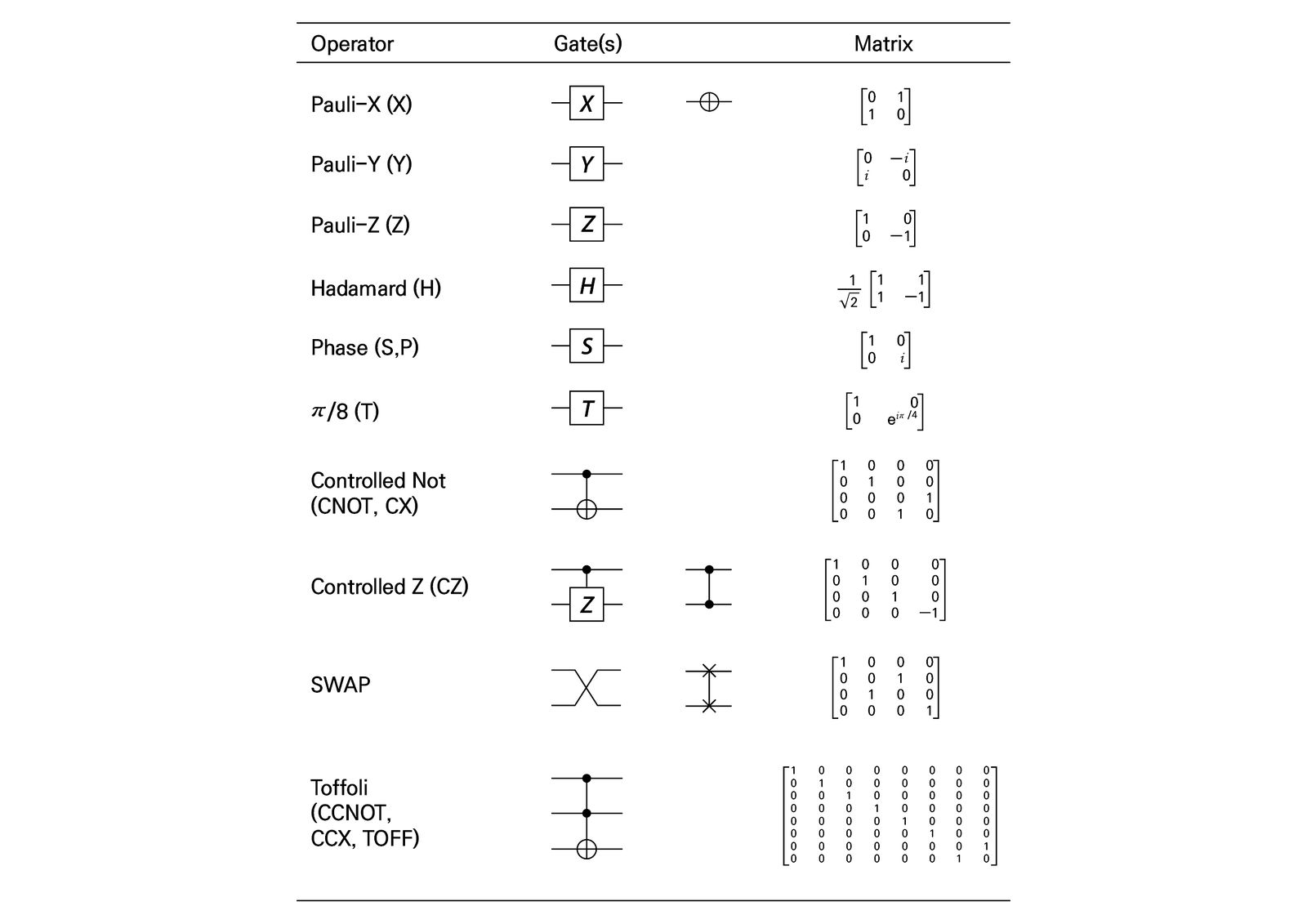
파울리 게이트(Pauli Gates)

X게이트: 큐비트 상태를 뒤집는 연산(고전 컴퓨터 NOT 유사)
Y게이트: 복소수 공간에서 큐비트 상태를 회전(y축 기존 180도 회전)
Z게이트: 큐비트의 위상을 변화시키는 연산

하다마드 게이트(Hadamard Gate, H)

큐비트를 0, 1 중첩 상태로 변환. 또는 순수 상태로 변환.
즉, 중첩이라면 순수 상태로, 순수 상태라면 중첩으로 변화시키는 연산
두 번 연산하면 원래 자기 상태로 돌아온다.

위상 게이트(Phase Gates)

S 게이트: 큐비트 위상 90도 회전
T 게이트: 큐비트 위상 45도 회전

CNOT 게이트(Controlled-NOT Gate)

고전 컴퓨터의 XOR 유사 -> XOR로 고전 컴퓨터의 모든 연산 가능
다중 큐비트 제어
첫 번째 큐피트(제어 큐비트)의 상태에 따라 두 번째 큐비트(대상 큐비트)의 상태를 뒤집는다. 양자 얽힘 생성할 때 사용.
제어 큐비트가 0이면 대상 큐비트는 그대로 통과
제어 큐비트가 1이면 대상 큐비트 반전
가역적. 즉 CNOT 게이트를 두 번 하면 원래대로 돌아감.

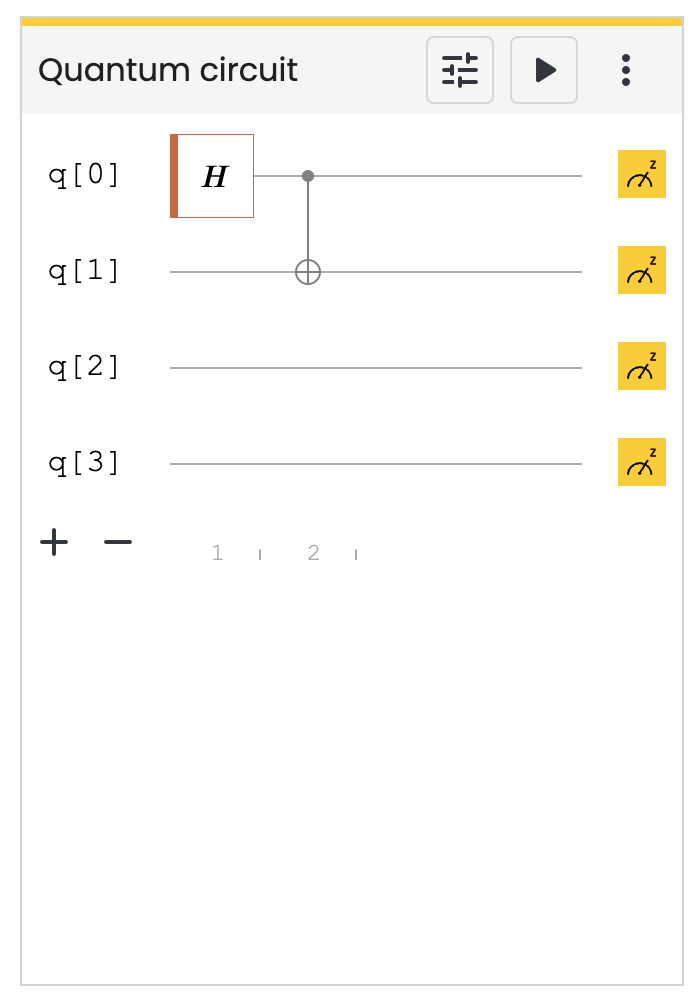
왜, 00, 01만 나오는지 이해 못했는데, 특별한 초기화 명령어가 없으면 0 상태로 시작한다고 가정함. 그럼 이해됨!

SWAP 게이트

두 큐비트의 상태를 교환

ClassBinu

다음 포스트

양자 컴퓨팅 개론