샤워하다가 모기 또 잡음..
모기 없어서 잘 잤다. 7:50 입실
어제 RB트리 삭제까지는 이제 이해함.
오늘은 C코딩 하기.
그래도 하다 보니까 C가 자연스럽게 녹아 드는 느낌이 남.. 다행..
RB Tree 어레이 구현
테스트 미통과 원인 찾음..
정렬이 안 되는 줄 알았는데
삽입 코드를 수정하면서 틀어진 거였음.
삽입 코드 다시 수정 후 테스트 통과.
node_t *rbtree_insert(rbtree *t, const key_t key)
{
node_t *new_node = (node_t *)(malloc(sizeof(node_t)));
if (new_node == NULL) {
print_malloc_failed();
return t->root;
}
new_node->color = RBTREE_RED;
new_node->key = key;
new_node->left = t->nil;
new_node->right = t->nil;
node_t *current = t->root;
node_t *parent = t->nil;
// 신규 노드 삽입될 위치 찾기
while (current != t->nil) {
parent = current;
if (key < current->key) {
current = current->left;
} else if (key > current->key) {
current = current->right;
} else {
current = current ->right;
}
}
// 신규 노드의 부모를 설정
new_node->parent = current;
if (parent == t->nil) {
t->root = new_node;
} else if (key < parent->key) {
parent->left = new_node;
} else if (key > parent->key) {
parent->right = new_node;
} else {
parent->right = new_node;
}
// RB Tree 특성 복구
rbtree_insert_fixup(t, new_node);
return new_node;
}삽입 여전히 틀렸음.
생각보다 빨리 찾았다!(2시간)
// 신규 노드의 부모를 설정
new_node->parent = parent; // new_node->parent = current 라고 잘못 적음.;
if (parent == t->nil) {
t->root = new_node;
} else if (key < parent->key) {
parent->left = new_node;
} else if (key > parent->key) {
parent->right = new_node;
} else {
parent->right = new_node;
}while문이 끝나면 while (current != t->nil) current는 항상 nil이다.
그래서 원래 코드에서는 신규 노드의 부모가 항상 nli이었던 것!
신규 노드의 부모 노드를 삽입 시 계속 내려오던 직전 노드, 즉 진짜 부모로 설정하니까 테스트 통과함..
(로컬이라서 valgrind는 아직 안 뜸. 이따 다 구현하고 서버 올려서 돌려봄.)
드디어 전체 테스트 통과!!!!
이건 최초 완성 코드임! 1차 리팩토링 코드는 여기있음.
https://velog.io/@classbinu/%ED%81%AC%EB%9E%98%ED%94%84%ED%86%A4-%EC%A0%95%EA%B8%80-3%EA%B8%B0-118%EC%88%98-TIL
#include "rbtree.h"
#include <stdio.h>
#include <stdlib.h>
void print_malloc_failed() { printf("메모리 할당에 실패하였습니다.\n"); }
rbtree *new_rbtree(void)
{
rbtree *t = (rbtree *)calloc(1, sizeof(rbtree));
if (!t) {
print_malloc_failed();
return NULL;
}
// T.nil을 생성합니다. 생성된 T.nil은 트리 내에서 계속 사용됩니다.
node_t *nil_node = (node_t *)calloc(1, sizeof(node_t));
if (!nil_node) {
print_malloc_failed();
free(t);
return NULL;
}
// T.nil의 멤버를 설정합니다.
nil_node->color = RBTREE_BLACK;
nil_node->parent = nil_node;
nil_node->left = nil_node;
nil_node->right = nil_node;
// 트리의 멤버를 설정합니다.
t->root = nil_node;
t->nil = nil_node;
return t;
}
void delete_rbtree(rbtree *t)
{
if (!t)
return;
// 스택 공간을 할당합니다.
node_t *stack[1024];
int stack_top = 0;
// 스택에 루트 노드를 넣고 스택 포인터를 +1합니다.
if (t->root != t->nil) {
stack[stack_top] = t->root;
stack_top++;
}
// 스택이 비어있을 때까지 반복합니다.
while (stack_top > 0) {
// 스택에서 노드를 pop합니다.
stack_top--;
node_t *node = stack[stack_top];
// 오른쪽 노드를 먼저 넣어서 전위 순회를 구현합니다.
// T.nil이 아니면 오른쪽 노드를 스택에 push합니다.
if (node->right != t->nil) {
stack[stack_top] = node->right;
stack_top++;
}
// T.nil이 아니면 왼쪽 노드를 스택에 push합니다.
if (node->left != t->nil) {
stack[stack_top] = node->left;
stack_top++;
}
// 꺼낸 노드를 해제합니다.
free(node);
node = NULL;
}
// 모든 노드를 해제 후에 T.nil을 해제합니다.
free(t->nil);
// 트리를 해제합니다.
free(t);
}
// 좌회전 함수
void left_rotate(rbtree *t, node_t *x)
{
if (x == t->nil || x->right == t->nil) {
return;
}
// y를 설정
node_t *y = x->right;
// y의 왼쪽 서브트리를 x의 오른쪽 서브트리로 옮긴다.
x->right = y->left;
if (y->left != t->nil) {
y->left->parent = x;
}
// y의 부모를 x의 부모로 변경한다.(y를 부모 자리로 승격)
y->parent = x->parent;
if (x->parent == t->nil) { // x가 루트였다면 승격된 y를 트리의 루트로 설정
t->root = y;
} else if (x == x->parent->left) { // x가 왼쪽 자식 노드였다면 승격된 y를 기존 부모의 왼쪽 자식으로 설정
x->parent->left = y;
} else { // x가 오른쪽 자식 노드였다면 승격된 y를 기존 부모의 오른쪽 자식으로 설정
x->parent->right = y;
}
// 승격된 y와 강등된 x의 관계를 설정
y->left = x;
x->parent = y;
}
// 우회전 함수
void right_rotate(rbtree *t, node_t *x)
{
if (x == t->nil || x->left == t->nil) {
return;
}
// y를 설정
node_t *y = x->left;
// y의 오른쪽 서브트리를 x의 왼쪽 서브트리로 옮긴다.
x->left = y->right;
if (y->right != t->nil) {
y->right->parent = x;
}
// y의 부모를 x의 부모로 변경한다.(y를 부모 자리로 승격)
y->parent = x->parent;
if (x->parent == t->nil) { // x가 루트였다면 승격된 y를 트리의 루트로 설정
t->root = y;
} else if (x == x->parent->left) { // x가 왼쪽 자식 노드였다면 승격된 y를 기존 부모의 왼쪽 자식으로 설정
x->parent->left = y;
} else { // x가 오른쪽 자식 노드였다면 승격된 y를 기존 부모의 오른쪽 자식으로 설정
x->parent->right = y;
}
// 승격된 y와 강등된 x의 관계를 설정
y->right = x;
x->parent = y;
}
void rbtree_insert_fixup(rbtree *t, node_t *z)
{
// 신규 노드가 루트면 끝 && 신규 노드의 부모 레드면 계속 체크
while (z != t->root && z->parent->color == RBTREE_RED) {
if (z->parent == z->parent->parent->left) { // 부모가 왼쪽 자식이라면
node_t *y = z->parent->parent->right; // 삼촌 노드 설정
if (y->color == RBTREE_RED) {
// 케이스1: z의 삼촌 y가 레드
z->parent->color = RBTREE_BLACK; // 부모 노드를 블랙으로 설정
y->color = RBTREE_BLACK; // 삼촌 노드를 블랙으로 설정
z->parent->parent->color = RBTREE_RED; // 조부모를 레드로 설정(부모와 삼촌에게 블랙을 물려줌)
z = z->parent->parent; // 레드로 설정된 조부모를 신규 삽입 노드로 취급
} else {
if (z == z->parent->right) {
// 케이스2: z가 오른쪽 자식인 경우(2는 궁극적으로 케이스 3이 됨)
z = z->parent; // 회전 기준을 z의 부모로 설정
left_rotate(t, z);
}
// 케이스 3: z가 왼쪽 자식인 경우
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
right_rotate(t, z->parent->parent); // 조부모를 기준으로 회전
}
} else { // 부모가 오른쪽 자식이라면(좌회전과 반대 코드)
node_t *y = z->parent->parent->left;
if (y->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
right_rotate(t, z);
}
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotate(t, z->parent->parent);
}
}
}
t->root->color = RBTREE_BLACK;
}
node_t *rbtree_insert(rbtree *t, const key_t key)
{
node_t *new_node = (node_t *)(malloc(sizeof(node_t)));
if (new_node == NULL) {
print_malloc_failed();
return t->root;
}
new_node->color = RBTREE_RED;
new_node->key = key;
new_node->parent = t->nil;
new_node->left = t->nil;
new_node->right = t->nil;
node_t *current = t->root;
node_t *parent = t->nil;
// 신규 노드 삽입될 위치 찾기
while (current != t->nil) {
parent = current;
if (key < current->key) {
current = current->left;
} else if (key > current->key) {
current = current->right;
} else {
current = current->right;
}
}
// 신규 노드의 부모를 설정
new_node->parent = parent;
if (parent == t->nil) {
t->root = new_node;
} else if (key < parent->key) {
parent->left = new_node;
} else if (key > parent->key) {
parent->right = new_node;
} else {
parent->right = new_node;
}
// RB Tree 특성 복구
rbtree_insert_fixup(t, new_node);
return new_node;
}
node_t *rbtree_find(const rbtree *t, const key_t key)
{
node_t *current = t->root;
while (current != t->nil) { // 현재 노드가 nil이 아니면 계속 검색
if (key == current->key) { // 찾았음
return current;
}
if (key < current->key) {
current = current->left; // 좌측 탐색
} else {
current = current->right; // 우측 탐색
}
}
// printf("일치하는 키가 없습니다.[%d]\n", key);
return NULL;
}
node_t *rbtree_min(const rbtree *t)
{
node_t *current = t->root;
while (current->left != t->nil) {
current = current->left;
}
return current;
}
node_t *rbtree_max(const rbtree *t)
{
node_t *current = t->root;
while (current->right != t->nil) {
current = current->right;
}
return current;
}
node_t *rbtree_min_in_subtree(rbtree *t, node_t *node)
{
if (node == t->nil) {
return t->nil;
}
while (node->left != t->nil) {
node = node->left;
}
return node;
}
node_t *rbtree_max_in_subtree(rbtree *t, node_t *node)
{
if (node == t->nil) {
return t->nil;
}
while (node->right != t->nil) {
node = node->right;
}
return node;
}
// 삭제된 노드의 서브트리를 삭제된 노드의 부모와 연결한다.
// u는 삭제할 노드, v는 삭제할 노드의 서브트리
void rbtree_transplant(rbtree *t, node_t *u, node_t *v)
{
if (u->parent == t->nil) {
t->root = v;
} else if (u == u->parent->left) {
u->parent->left = v;
} else {
u->parent->right = v;
}
v->parent = u->parent;
}
// rbtree 속성을 복구한다.
void rbtree_erase_fixup(rbtree *t, node_t *x)
{
node_t *w;
while (x != t->root && x->color == RBTREE_BLACK) {
if (x == x->parent->left) { // x가 왼쪽 노드이면 오른쪽 노드를 삼촌으로 설정
w = x->parent->right;
if (w->color == RBTREE_RED) { // 케이스1. 형제 w가 적색인 경우
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right; // 삼촌을 재설정해서 케이스 2,3,4로 변환
}
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) { // 케이스2
w->color = RBTREE_RED;
x = x->parent; // 이 시점에서 x가 블랙이면서 루트가 되면 루프가 종료
} else if (w->right->color == RBTREE_BLACK) {
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w); // 이 시점에서 케이스4로 변환
w = x->parent->right;
}
// 케이스 4. 케이스2의 일부 케이스를 제외하고 궁극적으로 모든 케이스는 4로 귀결됨.
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root;
} else {
w = x->parent->left;
if (w->color == RBTREE_RED) { // 케이스1. 형제 w가 적색인 경우
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left; // 삼촌을 재설정해서 케이스 2,3,4로 변환
}
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) { // 케이스2
w->color = RBTREE_RED;
x = x->parent; // 이 시점에서 x가 블랙이면서 루트가 되면 루프가 종료
} else if (w->left->color == RBTREE_BLACK) {
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w); // 이 시점에서 케이스4로 변환
w = x->parent->left;
}
// 케이스 4. 케이스2의 일부 케이스를 제외하고 궁극적으로 모든 케이스는 4로 귀결됨.
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
x->color = RBTREE_BLACK;
}
// 이진 검색 트리 방식으로 삭제
int rbtree_erase(rbtree *t, node_t *z)
{
// if (z == NULL || z == t->nil) {
// return -1;
// }
node_t *y = z;
node_t *x; // x는 삭제 연산으로 인해 부모 노드를 잃게 된 고아 노드
color_t y_original_color = y->color;
if (z->left == t->nil) { // 삭제할 노드의 왼쪽 자녀가 nil
x = z->right; // 삭제 과정에서 새롭게 올라온 노드를 기준으로 트리를 재조정함.
rbtree_transplant(t, z, z->right);
} else if (z->right == t->nil) { // 삭제할 노드의 오른쪽 자녀가 nil
x = z->left; // 삭제 과정에서 새롭게 올라온 노드를 기준으로 트리를 재조정함.
rbtree_transplant(t, z, z->left);
} else { // 삭제한 노드에 모두 자녀가 있음
y = rbtree_min_in_subtree(t, z->right); // 후계자 찾기
y_original_color = y->color;
x = y->right; // y의 왼쪽 자식은 무조건 nil이지만 오른쪽은 서브트리 존재 가능함
if (y->parent == z) { // 후계자가 삭제 노드의 직접 자식이라면, y는 이미 올바른 위치(y는 언제든지 떠날 준비가 되어 있음.)
x->parent = y; // x는 임시 변수로, y의 오른쪽 자녀로 등록되었지만, x의 부모가 누군인지는 아직 모름. 이 시점에서 연동.
} else { // y가 z를 대체하기 위해서는 y의 관계를 y의 오른쪽 자식에게 물려주고 떠나야 함.
rbtree_transplant(t, y, y->right); // y를 y의 오른쪽 자식으로 대체
y->right = z->right;
y->right->parent = y;
}
// z를 삭제(y로 대체)하고 기존 z의 왼쪽 자식의 관계를 y의 관계로 재설정
rbtree_transplant(t, z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
free(z);
z = NULL;
if (y_original_color == RBTREE_BLACK) {
rbtree_erase_fixup(t, x);
}
return 1;
}
void inorder_recursion(const node_t *node, key_t *arr, size_t *index, const node_t *nil)
{
if (node == nil)
return;
inorder_recursion(node->left, arr, index, nil);
arr[(*index)] = node->key;
(*index)++;
inorder_recursion(node->right, arr, index, nil);
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n)
{
if (t == NULL || arr == NULL)
return -1;
size_t index = 0;
inorder_recursion(t->root, arr, &index, t->nil);
if (index != n) {
return -1;
}
return 0;
}코드는 다시 리팩토링하면서 가독성과 성능 개선할 예정!
후.. 진짜 힘들고 머리 아팠지만 재미있음!
RB Tree 구현하면서 자연스럽게 C문법이 익혀지는 놀라움..
(잘한다는 건 아님)
예전에 유튜브 영상만 계속 봐도 이해 안 되던 개념들이 녹아드는 느낌..?
이제 테스트는 통과했으니까 코드를 계속 살펴보면서 RB Tree 확실하게 이해하고
C문법적인 내용도 훑어보기!
궁극적으로는 혼자서 C로 다시 구현하는 것 목표!
RB Tree 추가 학습
RB트리 삭제 시 대체자는 항상 블랙 노드일 수밖에 없다.
AVL 트리
왜 이름이 AVL 트리인가?
Adelson-Velsky and Landis 가 발명함.
스스로 균형을 잡는 트리
모든 노드의 균형도는 절대값 2미만이다.(-1, 0, 1만 가능)
균형을 어떻게 잡는가?
1. 균형도 계산
부모를 기준으로 좌측 노드 높이에서 우측 노드 높이를 뺀다.
부모 노드 높이는 자식 노드 중 가장 큰 값에서 +1을 한 값이다.
균형도가 -1보다 작으면 우측으로 쏠린 것, 균형도가 1보다 크면 좌측으로 쏠린 것.
2. 균형도가 2이상이면 회전을 통해서 균형 맞춤.
이건 BST 회전하고 똑같음.
일자로 뻗어 있으면 조부모를 회전하면 끝
꺾여 있으면 부모를 회전하고, 다시 조부모를 반대로 회전
장점과 단점은?
AVL의 장점
1. 더 엄격한 균형, 모든 노드의 균형이 -1, 0, 1이어야 함.(즉, 다른 서브 트리와 차이가 최대 1)
-> 검색, 삽입, 삭제의 평균 및 최악의 시간 복잡도가 O(log N)이다.
2. 높이가 낮아서 검색이 더 빠르다.
ABL의 단점
1. 빈번한 균형 재조정으로 인한 오버헤드
2. 균형 인수 저장에 따른 메모리 오버헤드
포인터 추가 학습
함수 호출 방식
1. Call by Value (값에 의한 호출)
함수의 인수 전달 방식은 기본적으로 '복사' 방식이다.
함수 내부에서 매개변수 변경해도 원본 변수 영향 없음.
그 이유는?
함수가 호출되면 함수마다 스택 프레임이 생긴다.
당연히 해당 스택 프레임에서 변경된 값이 해당 스택 프레임에만 영향을 미치며,
호출자의 스택 프레임에는 영향을 미치지 않는다.
콜 바이 밸류는 함수 간의 독립성과 안정성을 제공하며, 오류와 버그 방지에 도움이 된다.
하지만 복사로 인한 메모리 성능 측면에 부담이 되며, 복사 시간이 걸린다.
데이터 크기가 큰 경우에는 참조에 의한 호출을 사용할 수 있다.
2. Call by Address(참조에 의한 호출)
함수에 인수 전달할 때 해당 인수의 메모리 주소(참조)를 전달하는 방식
인수의 복바존이 만들어지지 않고, 전달된 주소로 원본 데이터 직접 접근
메모리 사용지 효율적이며, 큰 데이터도 복사하지 않고 함수로 전달할 수 있다.
복사가 발생하지 않으므로 값에 의한 호출보다 속도가 빠르다.
함수 내부에서 원본 데이터가 변경될 수 있으므로 부작용 주의해야 한다.
주로 포인터나 레퍼런스를 사용하여 메모리 주소를 전달하는 방식이다.
1차원 배열과 포인터
배열의 이름은 포인터이다!!!!
그래서 배열 이름 자체는 포인터 변수에 할당할 수 있다.
int a[5] = {1, 2, 3, 4, 5};
int *p;
p = a; // 가능즉, 배열이 포인터 자체이기 때문에 함수에 배열을 넘길 때는 포인트 변수로 받아와야 함.
일반 배열은 싱글 포인터로 받을 수 있음.
퀴즈에서 나왔던 코드 예시
#include <stdio.h>
void func(int *p, int n)
{
for (int i = 0; i < n; i++)
{
*p = *p + 1;
p++;
}
}
int main()
{
int arr[5] = {1, 2, 3, 4, 5};
func(arr, 5);
for (int i = 0; i < 5; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}결과적으로는 포인터나 배열이나 똑같은 개념이지만,
포인터를 정확히 쓸 줄 몰라서 배열의 인덱스로 처리함.
퀴즈 후에 복기하면서 포인트 연산에 대해서 핸즈 온.
확실히 손으로 해 본 것과 하지 않은 것은 완전 차이남.
포인터 배열
포인터 변수 선언
int *p1, *p2, *p3, *p4, *p5;
int *p[5]; int a=3;이차원 배열
포인터 변수(배열)을 선언할 때, 이차원 배열은 해당 포인터가 배열에 접근할 때
메모리를 얼마씩 더 뛰어야 하는지 알려줘야 함.
크기가 2인 배열을 가리키는 포인터
int (*p)[2];
// 포인터 변수를 선언하는데 원래 int는 4바이트씩 읽어오지만,
// [2]를 추가하면 8바이트씩 읽어 옴.
// 2개의 int값을 가리키는 배열의 메모리 주소를 할당할 수 있음.
// 주의할 점은 p는 여전히 int 타입이라는 것.이차원 배열은 안직 잘 모르겠음.
C언어 책으로 추가로 학습할 예정.
const
포인터 변수는 기본적으로 두 가지 값을 변경할 수 있다.
1. 포인터(메모리 주소) 자기 자신
2. 포인터가 참조하는 메모리의 값
const는 상수화(변경 불가능한 값)으로 선언하는 것
포인터 변수에서 const는 위치에 따라 무엇을 상수화하는지가 달라짐.
1. 포인터가 참조하는 값 상수화
const int *p = &a;
*p = 2; // 에러 발생2. 포인터 자체를 상수화
int *const p = &a;
p = &b; // 에러 발생3. 값과 포인터를 모두 상수화
const int *const p = &a;함수 포인터
함수 포인터 선언 방법
// 반환_타입 (*포인터_이름)(인자_타입1, 인자_타입2, ...);
void (*ptr)(char); // 함수 포인터 변수 선언
ptr = doNothing; // 함수 주소 포인터에 할당
doNothin('a'); // 원래 호출
ptr('a'); // 함수 포인터를 이용한 호출 배열이 포인트였다면, 함수도 포인터다!!!
구조체
여러 개의 타입을 묶어서 새로운 타입을 만드는 것
즉, 자료형을 정의하는 것
비유하자면 가방에 물건을 담는 것.
가방이 없으면 물건을 하나하나 다 들고 다녀야 됨.
#include <stdio.h>
struct student
{
char name[10];
char phone[20];
char gender;
int score;
};
int main()
{
int a;
struct student s1;
s1.score = 100;
a = s1.score;
printf("%d\n", a);
return 0;
}구조체는 세미콜론으로 마무리 해야 함.
구조체는 자료형을 정의하는 것일 뿐, 아직 메모리가 할당된 건 아니다.
즉, 구조체를 정의할 때 각 멤버에 초깃값을 할당하는 건 불가능하다.
구조체 변수가 아니라 포인터로 멤버에 접근해야 할 때는
->로 접근할 수 있다.
즉,구조체.멤버로 접근하거나,구조체 포인터->멤버로 접근한다.
C의 문자열
c는 문자열을 담는 특별한 자료형이 있는 건 아님.
포인터 변수에 해당 문자열의 첫 번째 주소를 저장하고, \0을 만나면 읽지 않는 것.
char *와 char[]는 완전히 동일한 말이다.
문자열을 출력할 때는 내부적으로 반복문을 통해서 구현된다고 함.
char *str1 = "Hello, world!";
char[] = "Hello, world!"; #include <stdio.h>
int main()
{
char *str = "Hello, world!";
printf("%s", str);
return 0;
}왜 출력할 때 *str이 아니라 str을 쓰지?
역참조를 해서 넘겨줘야 하지 않나?
아님! printf 함수 자체가 넘겨받은 메모리 주소부터 값을 읽어와서 출력하며
종료 문자(\0)을 만날 때까지 출력한다고 함.
그럼 여기서 드는 의문, 그럼 int 배열도 시작주소만 지정하면 알아서 다 출력하나?
실험해 본다!
#include <stdio.h>
int main()
{
int nums[] = {0, 1, 2, 3, 4};
printf("%d", nums);
return 0;
}결론: 안 됨
문자열만의 특별한 기능이라고 한다.
다른 배열을 출력할 때는 반복문으로 출력해야 한다.
scanf 연습
#include <stdio.h>
int main()
{
int x;
int y;
int z;
printf("숫자 3개를 입력하세요: ");
scanf("%d", &x);
scanf("%d", &y);
scanf("%d", &z);
int result = x + y + z;
printf("%d\n", result);
return 0;
}연산자
증감 연산자
++, --
전치 연산: 피연산자를 증감시킨 후, 연산을 수행
후치 연산: 연산을 먼저 수행한 후, 피연산자 값을 증감시킴.
#include <stdio.h>
int main()
{
int a = 3;
int b;
b = a++;
printf("%d\n", b); // 3
printf("%d\n", a); // 4
a = 3;
b = ++a;
printf("%d\n", b); // 4
printf("%d\n", a); // 4
return 0;
}전치 연산, 후치 연산 풀어보기
// 후치 연산
b = a++;
// 후치 연산 풀어보기
b = a;
a = a + 1;
// 전치 연산
b = ++a;
// 전치 연산 풀어보기
a = a + 1;
b = a;조건 연산자
변수 = 조건식 ? 식1 : 식2
#include <stdio.h>
int main() {
int x = 5;
int y = 10;
int max;
max = (x > y) ? x : y; // x가 y보다 크면 x를, 그렇지 않으면 y를 max에 할당
printf("더 큰 수는: %d\n", max);
return 0;
}형변환 연산자
형변환은 명시적 형변환(Casting)과 암시적 형변환(Type Conversion, Type Coercion)이 있음.
명시적 형변환
double num = 3.14;
int integerPart = (int)num; // 실수를 정수로 형변환암시적 형변환
int x = 5;
double y = 2.5;
double result = x + y; // 정수 x가 자동으로 실수로 형변환형변환은 데이터 손실이 발생할 수 있으므로 주의!
또한 데이터 타입 간에 호환 가능한 경우에만 사용해야 함!
(예를 들어 정수 <-> 실수는 의도에 따라 사용할 수 있지만,
문자 <-> 정수는 의도치 않는 결과를 가져올 수 있음.)
비트 연산자
논리 연산
AND : &
OR : |
XOR : ^
~ : NOTAND, OR, XOR은 항이 2개 있어야 하는 이항연산자이다.
NOT은 단항 연산자이다.
왜 C에서 and와 or는 각각 &&, ||로 부호를 두 개씩 쓰는가?
비트 연산자를 보고 의문이 해소됨!
논리 연산자는 &&, ||이고
비트 연산자는 &, | 이다!
시프트 연산
<< 좌측 이동 : 수가 커짐(MSB쪽으로 비트가 옮겨짐, 한칸 이동 시 2배)
>> 우측 이동 : 수가 작아짐(LSB쪽으로 비트가 옮겨짐. 한칸 이동 시 1/2배)
시프트 연산 후 범위를 벗어나는 비트는 버려짐.
새롭게 생겨나는 공간은 0으로 채워짐.
MSB, LSB가 뭐야?
MSB(Most Significant Bit) : 가장 높은 자리(중요)의 비트(가장 왼쪽)
LSB(Lease Significant Bit) : 가장 낮은 자리의 비트(가장 오른쪽)
왜 MSB는 중요한 자리인가?
보통 MSB의 자리에 위치한 비트가 수의 부호, 또는 데이터의 크기를 결정함.
int num = 5; // 0000 0101 (2진수)
int result = num << 2; // 왼쪽으로 2비트 이동
// 결과: 0001 0100 (2진수), 20 (10진수)
int num = -16; // 1111 0000 (2진수, 부호 있는 정수)
int result = num >> 2; // 오른쪽으로 2비트 이동
// 결과: 1111 1100 (2진수), -4 (10진수)리틀 엔디안 vs 빅 엔디안
바이트를 표기하는 순서
빅 엔디안
낮은 주소에 MSB(높은 비트)부터 저장하는 방식
일반적인 일상생활의 모습과 비슷한
리틀 엔디안
낮은 주소에 LSB(낮은 비트)부터 저장하는 방식
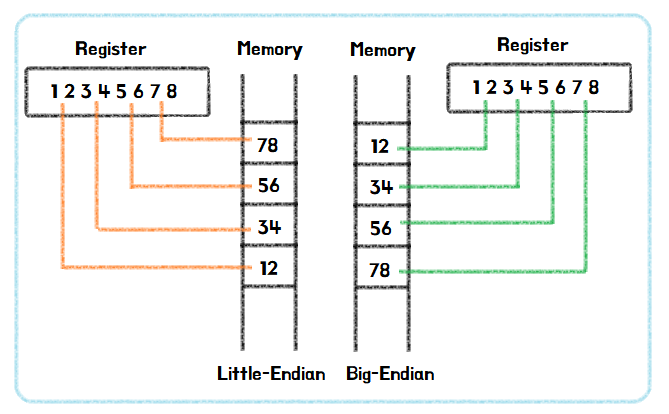
입출력 함수(버퍼)
버퍼는 임시 기억 공간으로 마트에서 카트와 같은 역할이다!
즉, 입력함수를 통해 커맨드라인에 뭔가 타이핑을 하는건
프로그램으로 전송되어 처리되는 게 아니라 우선 버퍼에 담기는 것!
그래서 썼다 지웠다는 빠르게 할 수 있음.
엔터를 치는 중간 버퍼에서 프로그램으로 전송되는 것!
버퍼가 필요한 이유!
CPU는 빠른데 입출력장치는 느리다.
데이터를 하나 하나 CPU와 통신하면 비효율적이다.
그래서 버퍼에 데이터를 모아서 준비가 되면 한번에 CPU와 통신해서 효율성을 높인다!
버퍼를 통해 CPU와 입출력장치의 속도 차이를 보완한다.
scanf()
scanf는 키보드로부터 입력을 받는 함수가 아니다.
버퍼에 있는 내용을 포맷에 맞게 꺼내 오는 함수다.
scanf("%c", &c); // 버퍼에서 1바이트를 꺼내 온다.getchar()
그냥 문자 한 글자만 받아오는 함수(정수, 실수는 못 받아 옴)
c1 = getchar();
while (getchar() != '\n'); // 버퍼를 비워주는 과정
// 버퍼를 비우지 않으면 개행문자(엔터) 같은 값이 들어가 있다.sanf, getchar는 버퍼에 데이터가 있으면 버퍼에서 값을 가져오고,
버퍼에 값이 없으면 커서를 깜빡이며 입력을 기다린다.
근데 버퍼에 그전의 개행 문자 같은 값이 있으면 입력을 받지 않고,
바로 이상한 값을 가져와 버린다.
그래서 버퍼를 비워줘야 한다.
버퍼를 이해하지 못하면 이 코드 정상 작동하지 않음
#include <stdio.h>
int main()
{
char ch;
printf("첫 번째 문자 입력: ");
scanf("%c", &ch); // 첫 번째 문자를 입력받는다. 여기서 Enter 키를 누르면 개행 문자('\n')도 버퍼에 들어감.
printf("첫 번쨰 문자는 %c\n", ch); // 버퍼에 '1'과 '엔터'가 들어가 있는데, scanf는 '1'만 가져와서 현재 버퍼에는 '엔터'가 들어가 있다.
printf("두 번째 문자 입력: ");
scanf("%c", &ch); // 버퍼에 '엔터'값이 있기 때문에 사용자에게 입력을 받지 않고 버퍼에 남아 있는 '엔터'값을 가지고 와서 ch변수에 넣는다.
printf("두 번째 문자는 %c\n", ch); // 개행문자가 출력된다.
return 0;
}키보드로 입력했을 때 그 버퍼는 어디에 있나?
버퍼는 하드웨어가 아니라 메모리에 상주하는 소프트웨어적인 공간이다.
키보드와 같은 표준 입력 장치는 표준 입력 버퍼라는 곳에 쌓인다.
문자열
문자열은 항상 마지막에 null(\0)이 들어간다.
그래서 글자수보다 1바이트가 더 큼.
printf("%s", "apple");
%s는 컴파일러가 주소로부터 null문자까지를 출력하라고 해석함.
널 문자는 아스키 코드에서 0이다!

문자열은 포인터, 배열 모두 사용할 수 있다.
이건 원래 문법적으로 안 맞는 거다.
상수 문자열이 원래는 주소니까 포인터 변수에 담아야 하는데,
하지만 문자열에 한하여 ""가 있으면 마지막에 널 문자를 추가하고,
배열 변수에 복사하는 방식으로 동작한다.
// 배열에 문자열 할당(복사) - 이건 원래 문법적으로 안 맞음
char str[7] = "banana";
// 그리고 이건 초기화와 동시에 할당해야지 유효함.
// 초기화 따로 할당 따로 하면 안 됨.
// 배열의 이름은 포인터 **상수**이다. 그니까 재할당이 안 됨.
// 포인터로 문자열 넣기
// 문자열 리터럴은 읽기 전용으로 저장됨.(읽기 전용 메모리에 저장)
#include <stdio.h>
int main()
{
char *str = "banana";
str[0] = 'a'; // 문자열 리터럴을 수정하려는 시도, 오류 발생
printf("%s", str);
}변수의 생존기간과 접근 범위
우선 가상 메모리의 영역부터 이해하고 가야 함.
프로세스는 1개의 가상 메모리를 갖게 되고, 이 가상 메모리가
스택, 힙, 데이터(BSS, GVAR), 코드 영역으로 나뉨.
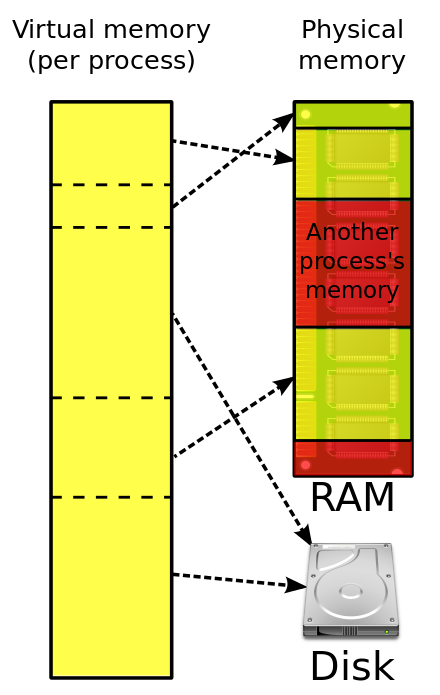
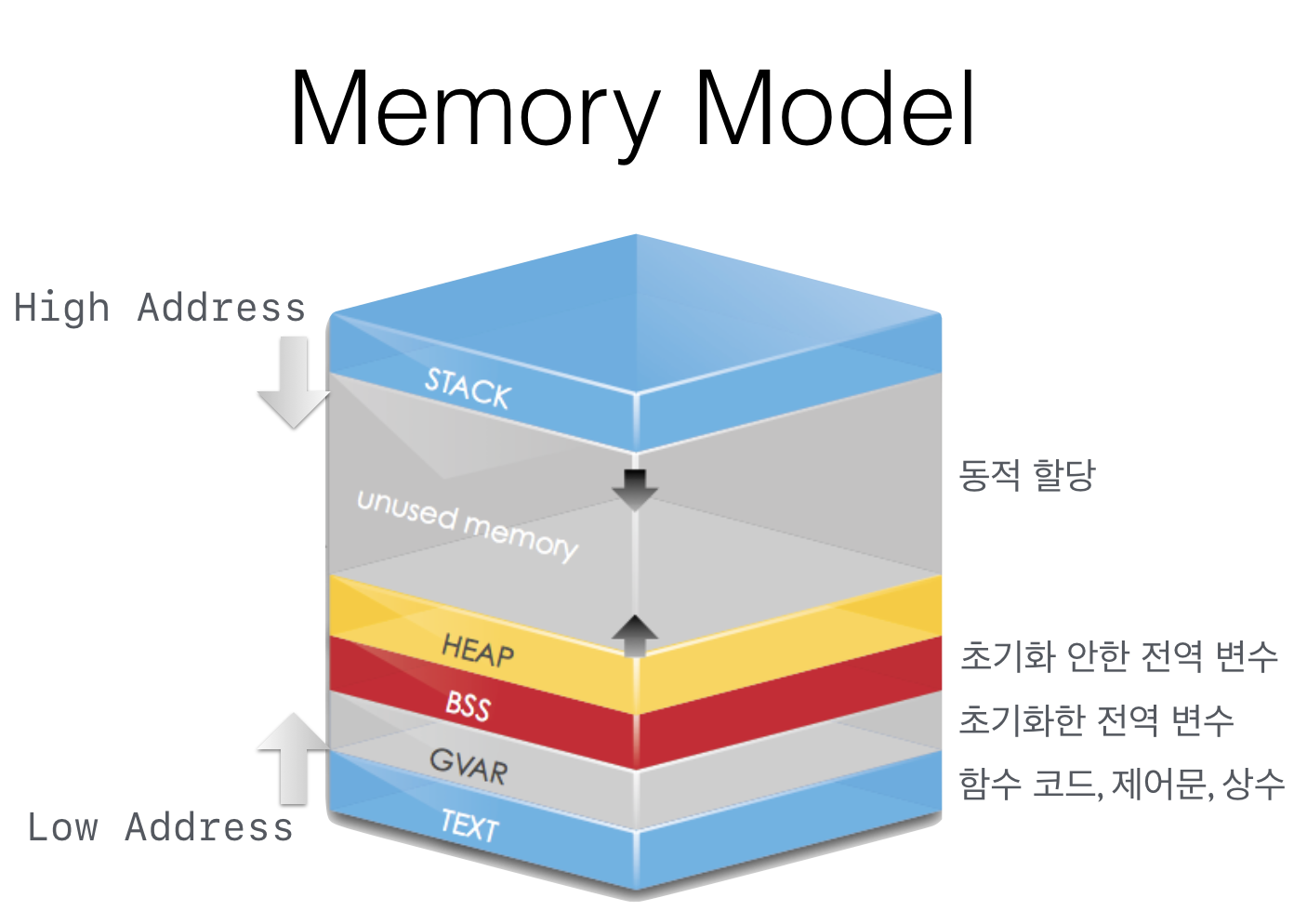
스택
함수 호출 관련 정보
호출 함수의 지역 변수, 함수 호출 스택 프레임 정보
지역 변수, 함수 매개 변수, 복귀 주소 등
힙
동적으로 할당된 데이터
데이터
전역 변수, 정적 변수(static)
코드(텍스트)
실행 코드(명령어)가 저장
CPU가 명령어 접근을 위해 접근하는 영역
프로그램 명령어 및 함수 코드
퀴즈 복기
포인터 문제는 풀었음.
대신 배열값을 바꾸는 걸 포인터로 익숙하지 않아서 인덱스로 썼음.
포인트로 배열 접근하고 조작하는 것 확실히 다시 익혀 보기
BST는 풀었는데, AVL은 확실히 몰라서 제출 못함.
RB는 어떻게 하긴 했는데 중간에 실수가 있었는지 정답하고 맞지 않음.
삽입, 삭제 시뮬레이션 안해본 게 바로 티가 남.
레드블랙 트리는 블랙노드 삭제만 봤는데,
그러다 보니 레드노드 삭제는 모르고 있었음..;
마지막 메모리 계산 문제는 char 유형 1개 틀림.
왜 char는 4바이트라고 생각했지..? 그냥 2만 더하면 될거는 8을 더함.
계산도 더 복잡했는데..
트리 삽입, 삭제는 눈으로만 보고 넘어가니까 확실히 시뮬레이션이 안 됨.
BST는 몇 번 연습해봤다고 금방 풀었음.
AVL, RB는 몇 가지 케이스로 익숙해지게 연습해 보자.
스터디
포인터 연산에서 헷갈리던거 팀원이 명쾌하게 알려줌!
*p + 1은 p가 가리키는 값을 가져와서 거기다가 1을 더하는 것
&p + 1은 p주소 값을 가져온 후 타입별로 1칸 늘리는 것(예를 들어 int는 +1이 +4바이트)
주의할 점은 그냥 저렇게 한다고 해서 원본 값이나 원본 주소가 변하지는 않음!
값을 변경시키고 싶으면 다시 재할당 해줘야 함.
