3D Point Clouds (or Geometric Graphs)
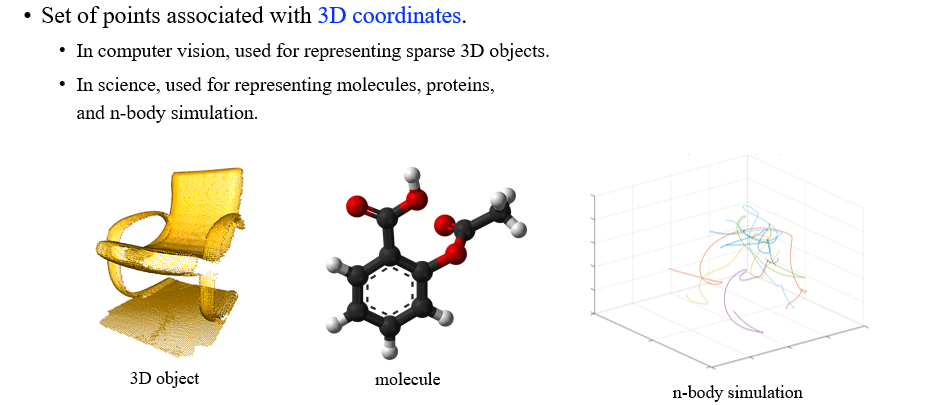3D geometric GNN은 3D graph data를 설명하는 framework로 가장 대표적인 data가 바로 3D point cloud이다. 3D 좌표에서 node vertex들이 표현되어 있는 graph를 3D point cloud라고 하고, 가장 대표적인 예시로 molecule data가 존재한다. Molecule은 실제로 굉장히 중요한 data로 3D 공간 상에서 정의될 수 있다.
3D 공간 상에 표현되는 molecule은 geometric graph로 정의되며, 이는 Euclidean space 상에서 3D point cloud data와 관련이 있다. 이는 permutation symmetry도 중요하지만 3D space 상에서 roation 등의 Euclidean symmetry도 고려해야 한다. Molecule을 3D 상에서 회전을 시켜도 identity는 보존되어야 한다. 그래서 이러한 data는 vertex들이 3D space 상에서 정의가 되며, 각 vertex는 3D space 좌표 정보와 각 vertex가 어떠한 타입인지 등에 관한 정보를 node feature로 가지게 된다. 그리고 이러한 graph 구조는 cut-off radius에 의해 결정이 되는데, 이는 곧 vertex 사이의 Euclidean distance가 얼마나 작은지와 관련이 있다.
E(3) Transformation
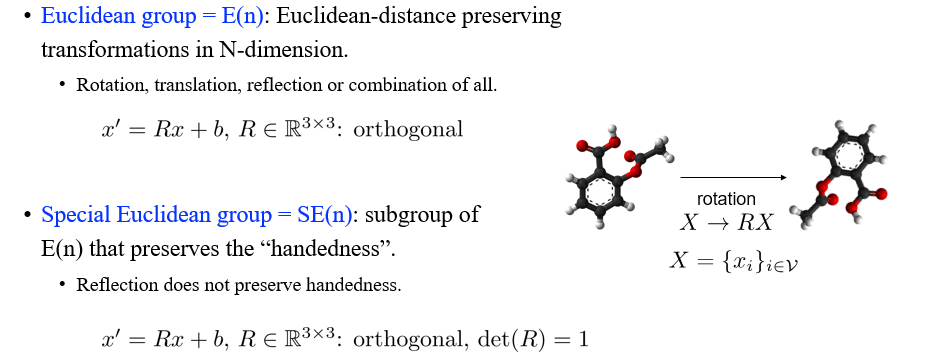이전에 살펴본 permutation symmetry와는 좀 다르게 3D graph에 대해서 Euclidean group transformation을 가지게 되고, 우리는 이를 E(3) Transformation이라 부른다. 여기서 E는 Euclidean을 의미하게 된다. Euclidean group은 또한 transformation들의 set으로, E(n)이라는 것은 Euclidean-distance를 보존하는 transformation들을 차원에서 정의하는 Euclidean group을 나타낸다. 아무래도 3차원에서 graph를 표현하기 때문에 E(3) transformation이라 하는 것이다. Rotation, translation, reflection으로 transformation을 구성할 수 있으며, 이들의 조합으로도 구성할 수 있다.
추가로 special Euclidean group SE(n)을 정의할 수 있다. 이는 handedness를 보존하는 E(n)의 subgroup을 의미한다. Euclidean group에서 단순히 reflection을 제외시킬 수 있다. 왜냐하면 손을 움직인다고 했을 때, 우리가 왼손과 오른손을 서로 바꿀 수가 없을 것이다. 실제로 object를 reflecting 시키는 것은 불가능하기 때문이다. 그래서 오로지 translation과 rotation만 가능한 group을 정의한 것이다. 현실을 반영한 SE(3) group은 중요한 개념인 셈이다. 우리는 앞으로 다루기 쉬운 E(3) group을 더 이야기해볼 것이다.
Designing DNNs for E(3) Transformations
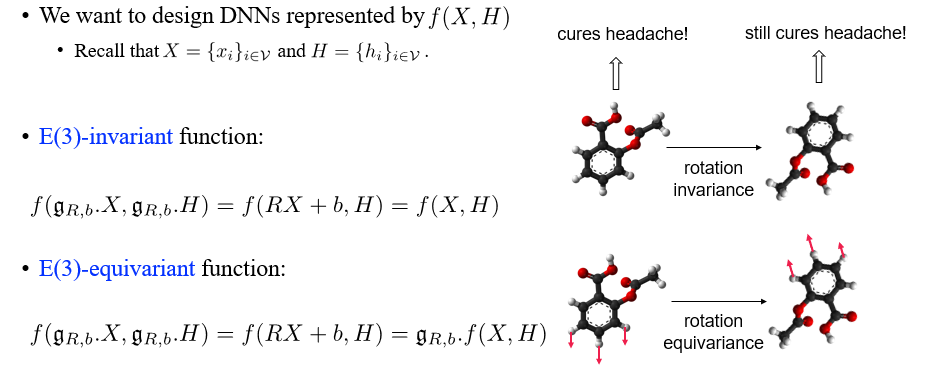우리는 에 의해 표현되는 DNN을 설계해볼 것이고, 여기에 invariant function과 equivariant function까지 설계해볼 수 있다. Invariant function의 경우에는 input 에 rotation matrix 을 곱하고 translation matrix 를 더해도 그 결과가 변하지 않으면 된다. 반대로 equivariant function의 경우 대응되는 output이 나오면 되는 것이다.
Main Applications
Drug Discovery
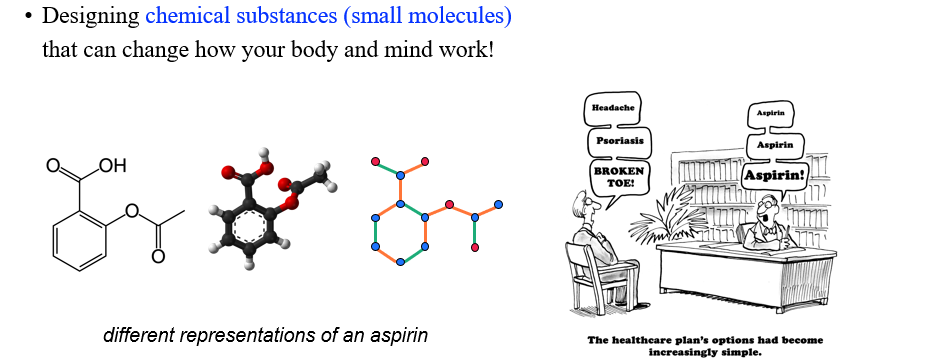지금부터는 이러한 3D graph를 활용한 여러 적용 분야들에 대해서 알아볼 것이다. Durg는 우리의 몸과 마음을 바꿔주는 chemical substance이다. 우리가 어떠한 목적에 맞는 drug를 발견하도록 하는 분야가 drug discovery이다. 하나의 neural network가 모든 drug를 발견하기를 원치는 않는다. 아무래도 속도적인 측면과 신뢰의 관점에서 하나의 network는 이 분야에서 한계가 존재한다.
How Drugs Work?
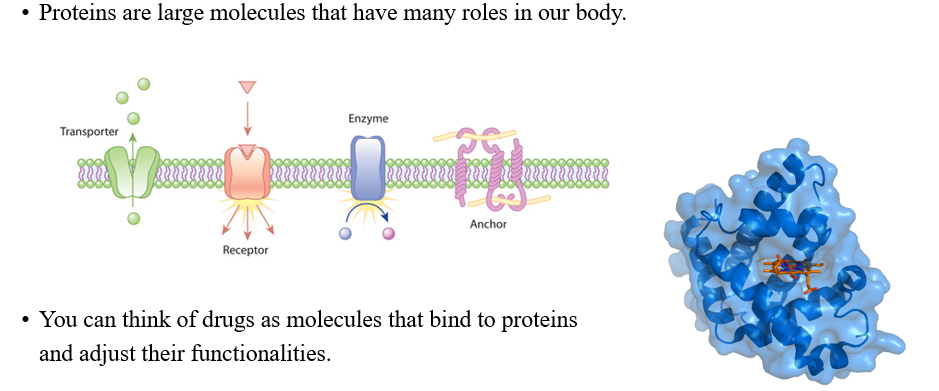만약 우리가 GNN을 drug discovery에 활용하고 싶다면, drug가 실제로 어떻게 동작하는지 이해할 필요가 있다. Drug는 사람의 몸에서 반응을 하고, 사람의 몸은 protein으로 구성되어져 있다. 여기서 protein은 molecule로 구성되며 많은 수의 atom으로 이루어져 있다. 각 atom은 다양한 기능을 가지고 있다. 그래서 특정 protein에 연결되는 drug를 찾아야하는 것이다. 작은 molecule이 transporter 앞에 멈춰서 특정 protein에 연결되도록 한다. 우리는 GNN을 molecule이 연결되는 과정으로 생각하고 설계하면 된다.
Drug Types
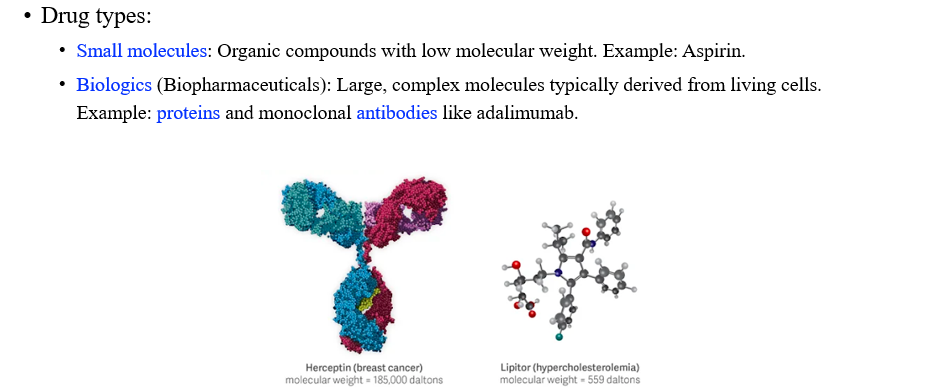우리는 2가지 종류의 drug를 생각할 수 있다. 하나는 small molecule이고 다른 하나는 biologic이다. 전자는 Aspirin과 같은 low weight를 가지는 organic compound이다. 그래서 protein에 비해서 적은 수의 atom을 가지고 있다. 후자는 반대로 더 큰 molecule로 구성될 수 있다. 그래서 이는 protein 기반의 drug들에 해당한다.
Small Molecule drugs
Small molecule은 ligand와 같은 역할을 한다. 사람들이 지금까지 대체로 small drug들에 관한 발견과 연구를 진행했기 때문에, 사람들은 더이상 발견될 small molecule drug가 없다고 생각한다. 즉, 사람들의 발견이 힘들기 때문에 인공지능 모델이 도움을 줄 수 있다는 것이다.
Biologics
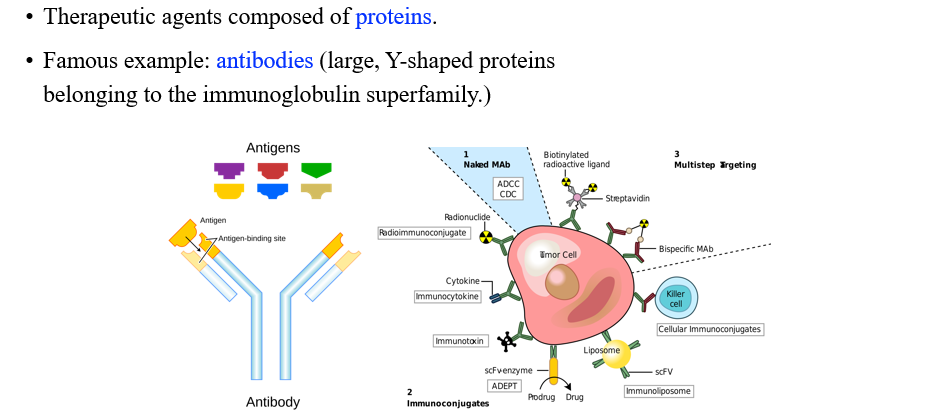Protein이 오히려 최근에 사람들이 찾고자 하는 drug에 해당한다. 대표적으로 antibody가 있을 수 있다.
Accelerating Molecular Simulation
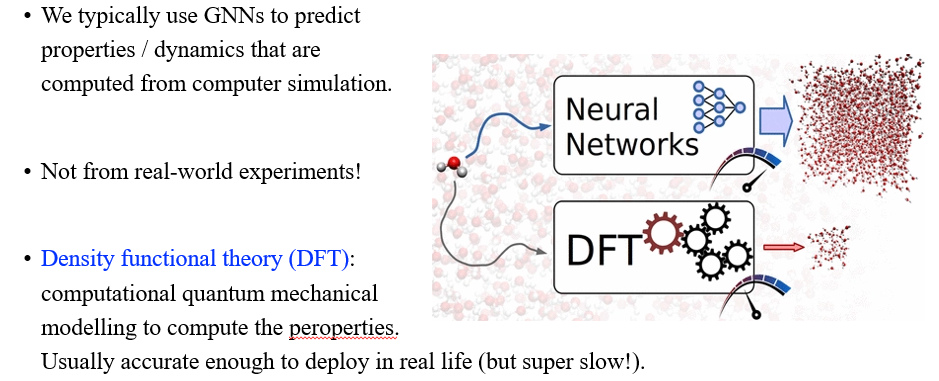그렇다면 GNN이 어떻게 drug discovery를 가속화하는데 이용될 수 있을까? 이는 molecular simulation으로 충분히 활용될 수 있다. 우리는 GNN을 이용해서 computer simulation으로부터 구해지는 property나 dynamic들을 예측할 수 있다. 이는 현실에서 실험되는 것과는 다르다. 현실에서 실험되는 부분과 관련해서는 density functional theory (DFT)라는 또다른 computer simulation을 이용하게 된다. 이는 super computer를 이용하며 cost가 많이 들고 속도가 많이 느리다. 이를 neural network로 대체하면 좋을 수 있지만, 아직 많은 한계점들이 존재한다.
Molecular Property Prediction
Molecular property prediction에 이용되는 대표적인 dataset으로 Quantum Machines 9 (QM9)이 있다. 이는 CHONF 원자들로 구성된 안정된 organic molecule들로 구성되어 있다.
Molecular Dynamics Simulation
진공 속에서 어떻게 molecule이 이동하는지 예측하는 molecular dynamics simulation에 사용되는 dataset으로는 Molecule Dynamics 17 (MD17)이 있다.
Material Property Prediction
현실과 그래도 밀접한 material property prediction에 사용되는 dataset으로 Open Catalysts 20 (OC20)이 있다. 위에서 빨간 공들이 catalyst이고 여기서 어떻게 작은 molecule이 동작하는지 예측하는 것이다.
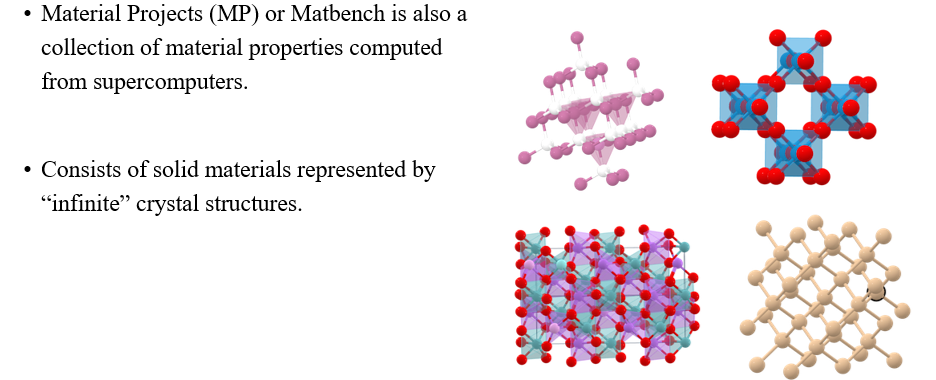Crystal과 관련해서는 Material Projects (MP) dataset이 존재한다.
Protein Structure Prediction
Protein이 주어졌을 때 3D 좌표를 예측하는 task도 존재한다.
Protein Docking
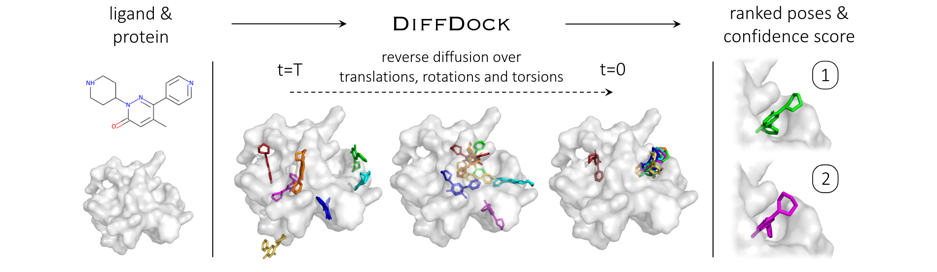Protein docking은 주어진 protein이 어떻게 연결이 될지를 예측하는 것으로 사람의 몸에서 일어나는 반응을 simulation할 수 있다. 어떠한 drug가 protein을 활성화 시킬지 확인할 수 있다. 하나의 drug molecule과 protein이 어떻게 연결되는지 simulation을 할 수 있다.
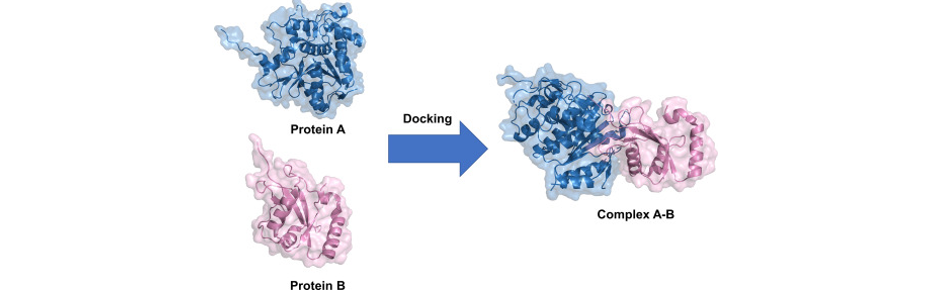위와 같이 두 protein이 docking되는지도 simulation을 통해서 확인할 수 있다.
