
Expander Graphs
 이번에는 over-squashing 현상과 관련하여 expander graph의 개념을 기반으로 해결하려는 expander graph propagation에 대해서 알아보고자 한다. 이는 negatively curved graph에 대한 이론적인 분석을 중심으로 구성되어 있어 흥미로운 부분이 많다. Over-squashing 현상은 graph의 toplogy에 따라 발생한다. 특히 negatively curved edge나 graph는 Cheeger constant와 관련이 있다. 여기서 graph의 bottleneck 현상을 수학적으로 정의한 이 constant 값이 작을수록 over-squashing 현상과 밀접한 연관성이 존재한다. 그렇다면 message passing을 위한 최적의 graph가 어떠한 상태여야하는지 궁금해하였다. 그것은 Cheeger constant 값이 큰 graph로, 이를 expander graph라고 정의하게 되었다.
이번에는 over-squashing 현상과 관련하여 expander graph의 개념을 기반으로 해결하려는 expander graph propagation에 대해서 알아보고자 한다. 이는 negatively curved graph에 대한 이론적인 분석을 중심으로 구성되어 있어 흥미로운 부분이 많다. Over-squashing 현상은 graph의 toplogy에 따라 발생한다. 특히 negatively curved edge나 graph는 Cheeger constant와 관련이 있다. 여기서 graph의 bottleneck 현상을 수학적으로 정의한 이 constant 값이 작을수록 over-squashing 현상과 밀접한 연관성이 존재한다. 그렇다면 message passing을 위한 최적의 graph가 어떠한 상태여야하는지 궁금해하였다. 그것은 Cheeger constant 값이 큰 graph로, 이를 expander graph라고 정의하게 되었다.
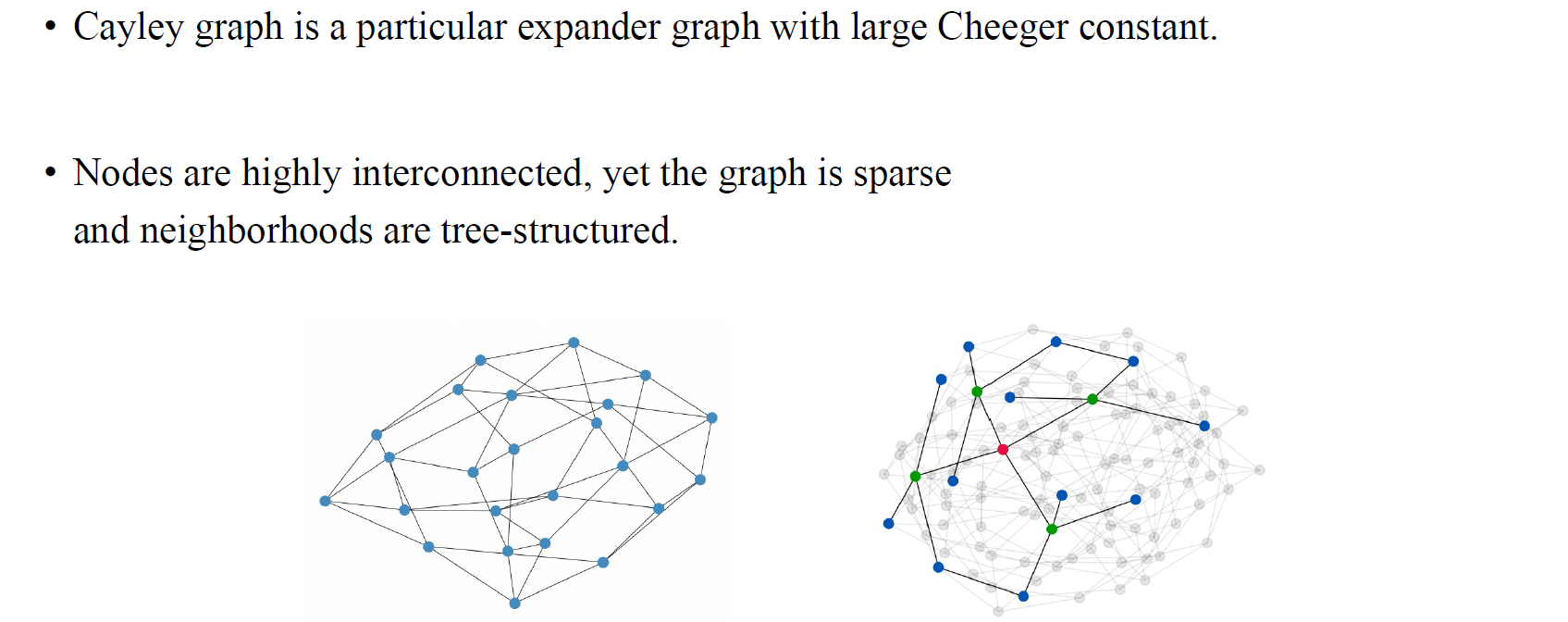 만약 expander graph가 message passing을 위한 최적의 graph라고 한다면, 어떻게 이것을 사용해야 좋은 결과를 얻을 수 있을지를 저자들은 설명했다. 아이디어는 굉장히 단순하다. 주어진 graph에서 시작해서 message passing을 적용하기 위해서 expander graph를 사용하고 다시 원래의 graph로 돌아오고 다시 expander graph를 사용하는 식의 방식으로 동작하게 된다. 이들은 가상의 message passing 기법을 추가한 것이다. 여기서 이들은 Cheeger constant 값이 큰 expander graph인 Cayley graph를 사용했다. 이 graph는 node들이 상당히 interconnected 되어 있기 때문에 어떠한 vertex 쌍을 선택하더라도 이들을 연결하는 path가 존재하게 될 것이다. 전체적으로 graph 상에서 path의 분포가 고르게 존재하게 되는 것이다. 이러한 graph는 interconnection이 잘 되어 있지만, 아직 sparse하고 이웃들간 지역적으로 tree의 구조를 보이는 것이 이 graph의 특징이다.
만약 expander graph가 message passing을 위한 최적의 graph라고 한다면, 어떻게 이것을 사용해야 좋은 결과를 얻을 수 있을지를 저자들은 설명했다. 아이디어는 굉장히 단순하다. 주어진 graph에서 시작해서 message passing을 적용하기 위해서 expander graph를 사용하고 다시 원래의 graph로 돌아오고 다시 expander graph를 사용하는 식의 방식으로 동작하게 된다. 이들은 가상의 message passing 기법을 추가한 것이다. 여기서 이들은 Cheeger constant 값이 큰 expander graph인 Cayley graph를 사용했다. 이 graph는 node들이 상당히 interconnected 되어 있기 때문에 어떠한 vertex 쌍을 선택하더라도 이들을 연결하는 path가 존재하게 될 것이다. 전체적으로 graph 상에서 path의 분포가 고르게 존재하게 되는 것이다. 이러한 graph는 interconnection이 잘 되어 있지만, 아직 sparse하고 이웃들간 지역적으로 tree의 구조를 보이는 것이 이 graph의 특징이다.
Expander Graph Propagation
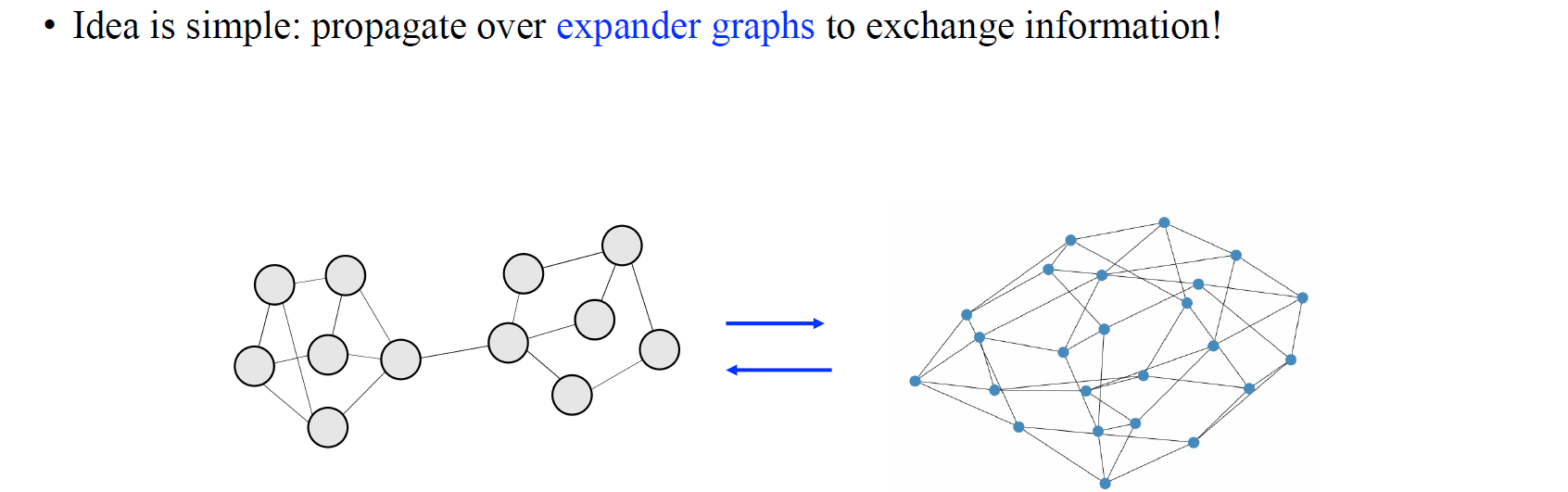 다시 아이디어를 살펴보면 매우 간단하다. 주어진 input graph가 over-squashing 현상을 가지고 있는 상태에서 원래의 GNN을 가지고 첫번째 layer를 update한 다음에 두번째 layer의 경우에는 expander graph를 이용해서 update하는 것이다. 이러한 과정을 계속해서 반복하면 expander graph propagation이 된다. Expander graph를 사용해서 vertex 쌍의 정보를 모두 가지게 되어 over-squashing 현상을 완화할 수 있다.
다시 아이디어를 살펴보면 매우 간단하다. 주어진 input graph가 over-squashing 현상을 가지고 있는 상태에서 원래의 GNN을 가지고 첫번째 layer를 update한 다음에 두번째 layer의 경우에는 expander graph를 이용해서 update하는 것이다. 이러한 과정을 계속해서 반복하면 expander graph propagation이 된다. Expander graph를 사용해서 vertex 쌍의 정보를 모두 가지게 되어 over-squashing 현상을 완화할 수 있다.
 원래의 graph와 Cayley graph를 번갈아 사용하는 것이 결국 이 방식의 전부인 것이다.
원래의 graph와 Cayley graph를 번갈아 사용하는 것이 결국 이 방식의 전부인 것이다.
