The Weisfeiler-Lehman (WL) Test
Weisfeiler-Lehman (WL) test는 원래 neural network와 관련된 개념이 아니라 graph theory에서 사용되는 개념이다. 이는 graph isomorphism에 관심을 두며, graph isomorphism 문제는 polynomial time에 해결되지 않는 NP intermediate라고 한다. Polynomial time 안에 해결되는 알고리즘을 우리는 모르며 또한 NP complete인지도 잘 모른다. WL test는 이 문제를 해결하기 위해서 사람들이 heuristic하게 만든 알고리즘 중 하나이다. Graph isomorphim 문제를 시험해보고 싶으며, 두 graph가 isomorphism을 만족하는지 결론을 내고자 한다. WL test가 polynomial time에 해당하기 때문에 graph isomorphism 문제를 풀지는 못할 것이다. 그러나 만약 두 graph가 WL test에 의해서 구분이 된다면, 두 graph가 non-isomorphic하다고 결론지을 수가 있다. WL test는 두 graph가 non-isomoprhic하여 다르다는 것을 보장을 해주는 수단이다. 한편, WL test가 두 graph를 구분하는데 실패할 수 있을 것이다. 이때는 어떠한 결론도 낼 수 없게 된다. 두 graph가 isomorphic한지 non-isomorphic한지 그거는 아무도 모른다는 것이다.
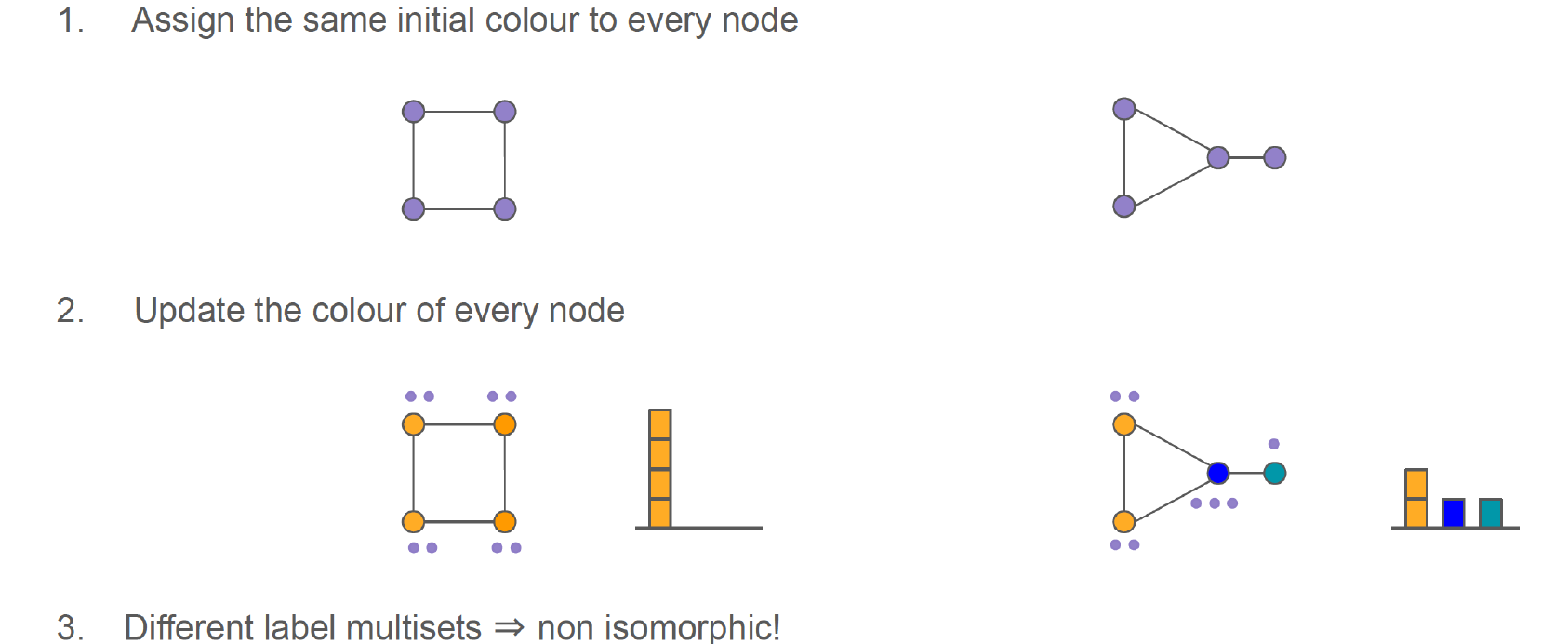그렇다면 WL test는 어떻게 동작할까? 우리는 이를 수식적으로 설명할 수도 있지만 직관적으로 그림을 통해서 보는게 이해하기는 더 쉬울 것이다. GNN과 유사하도록 heuristic하게 동작하게 된다. WL test는 GNN처럼 message propagation을 하고 이를 여러 layer에서 반복하게 된다. 주어진 graph에 대해서 가장 첫번째 iteration을 거치면 모든 vertex가 동일하다고 판별될 것이다. 모든 node에 초기의 color를 할당하게 될 것이다. 위의 예시를 보면 2개의 graph에 대해서 모든 node에 보라색이 할당된 것을 볼 수 있다. 그리고 GNN과 비슷하게 각 layer마다 각 node에 할당된 color를 update하게 된다. 다시 위의 예시를 보면 좌측 graph는 각 node가 2개의 node와 연결되어 있기 때문에 모두 주황색을 할당받게 되었다. 반면 오른쪽 graph에서는 2개의 node와 연결되어 있는 node가 2개 있고, 나머지는 각각 3개와 1개가 연결되어 있다. 3개가 연결된 node는 파란색을, 1개가 연결된 node는 초록색을 할당받게 되었다. 이러한 과정이 두번째 iteration에서 수행되었다. 만약 두 graph가 isomorphic하다면 이러한 상황이 발생하지 않았을 것이다. 따라서 우리는 위의 예시에서 제시된 2개의 graph가 non-isomorphic하다는 결론을 낼 수 있다.
이번에는 다른 예시를 보도록 하자. 위의 2개의 graph에 대해서 WL test를 수행하게 되면 첫번째 iteration에서는 모두 보라색을 할당받지만, 두번째 iteration에서는 degree에 따라 주황색과 파란색을 할당받게 외었다. 그 결과 두 graph 모두 4개의 주황 vertex와 2개의 파란 vertex를 할당받은 것을 볼 수 있다. 첫번째 예시와 다르게 두번째 예시에서는 두번의 iteration 후에 두 graph가 isomorphic한 것을 확인할 수 있었다.
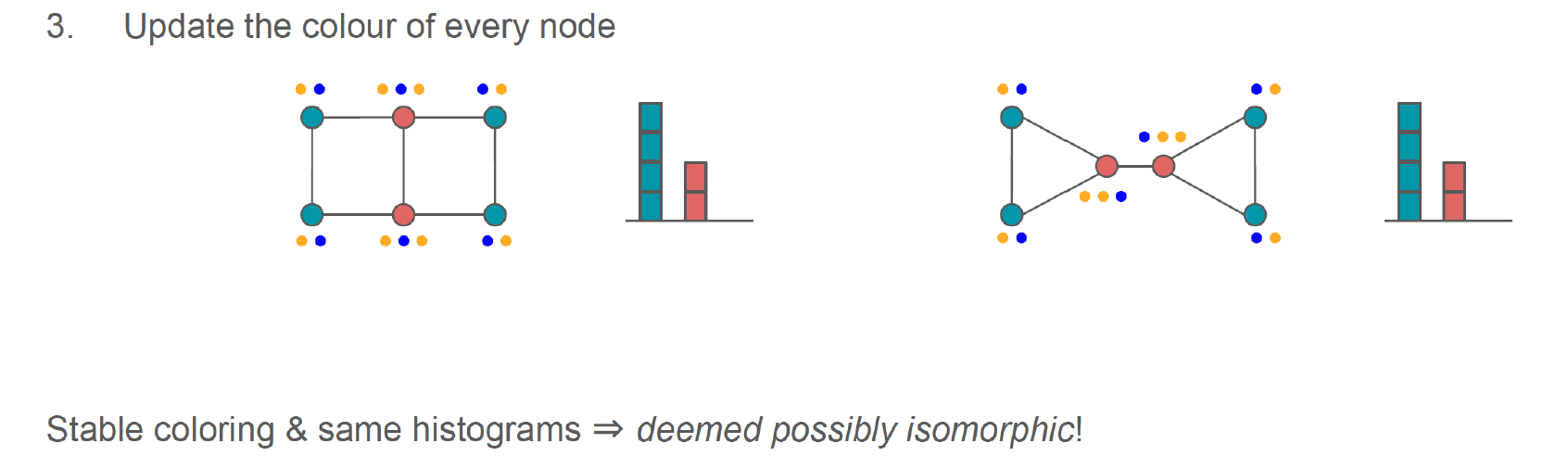세번째 iteration을 해보면 1개의 주황 vertex와 1개의 파랑 vertex와 연결된 vertex에는 초록색을, 2개의 주황 vertex와 1개의 파란 vertex와 연결된 vertex에는 빨간색을 할당했다. 그 결과 두 graph가 동일한 결과를 만들었고, 따라서 두 graph가 isomorphic하다고 이야기할 수 있게 되었다.
WL test는 이웃 vertex의 color를 통해서 해당 vertex의 color를 update할 수 있다. 그리고 계속해서 반복하다보면 안정된 상태로 수렴하는 것을 확인할 수 있고, color의 distribution이 동일해지는 것도 확인할 수 있게 된다. 이러한 상황이 오게 되면 WL test를 통해서 두 graph를 구분하는 것에 실패했다고 볼 수 있다. WL test를 했음에도 두 graph가 동일해보이기 때문이다.
이제 이를 수식으로 정리해보자. 우선 2개의 graph 가 주어지면 모든 node에 동일한 color 를 가장 먼저 할당하게 된다. Color가 안정될 때까지 color를 update하는 과정이 반복되는데, 이때 위와 같이 강력한 hashing function HASH에 의해 vertex의 color는 update하게 된다. Vertex 의 color 가 현재 iteration 에서 update되기 위해서는 본인의 color 와 이전 단계의 neighbor vertex 의 color 를 이용해서 진행된다. 우리는 2개의 set function에 대해서 hash하려고 할 것이고, 따라서 우리는 2개의 set을 비교할 수 있다는 것을 가정할 수 있다. 만약 두 set이 서로 다르다고 한다면, 즉 distribution이 서로 다르다고 한다면, 두 graph가 non-isomorphic하다고 결론낼 수 있다. 만약 color들이 동일한 distribution으로 수렴하게 된다면, 우리는 어떠한 결론도 낼 수 없다.
Are All GNNs Made Equal?
이러한 WL test는 GNN과 매우 흡사하기 때문에 우리에게 있어 매우 유용하게 사용된다. WL test가 어떠한 상황에서는 GNN보다도 강력하게 동작할 수 있다. WL test가 강력한 HASH function을 평가한다고 가정하기 때문에 어떠한 set도 구분할 수 있게 된다. 예를 들어 2개의 주황색과 1개의 파란색을 빨간색으로 대응시키는 것은 아주 강력한 function이 된다. GNN이나 어떠한 MLP도 이러한 function을 학습할 수 없다. 그래서 HASH function은 상당한 힘을 지니고 있다.
MPNN이 WL test와 유사하게 동작할 수 있을까? WL test와 유사하게 동작한다는 것은 WL test는 구분할 수 있는 graph를 MPNN이 구분할 수 있는지를 의미한다. 그리고 사람들은 WL test가 graph convolution을 사용하는 MPNN에 의해 나타낼 수 없다는 것을 알아냈다. 여기서 우리는 실제로 WL test처럼 동작하고자 한다면 graph isomorphism network (GIN)이라고 불리는 모델이 필요하다는 것을 알게 되었다. GIN은 WL test를 동작시키기 위해서 설계된 모델이다. 이 방법의 아이디어는 color를 셀 수 있는 SUM aggregator가 필요하다는 것이다. GCN은 이웃들의 정보를 average화 시키기 때문이다. 또 다른 아이디어는 update function에 MLP를 사용해야 한다는 것이다. 왜냐하면 MLP가 보편적으로 강력하기 때문에 HASH function처럼 동작할 수 있다. 이렇게 SUM aggregator를 사용하고 linear operator를 MLP로 대체함으로써 GIN이 나타나게 되었다. 그리고 GIN이 WL test만큼 강력하다는 것을 이론적으로 보였으며, GCN이 WL test보다 덜 강력하다는 것을 이야기했다. 놀랍게도 GIN이 실제로 더 강력한 경우가 다수 존재했다.
