[그래프 기계학습] Over-Squashing Problem

MPNN Formalism

오늘 알아볼 내용은 GNN의 이론적인 분석에서 꽤 비중이 있는 paradiam에 대해서 알아볼 것이다. 바로 over-squashing 문제이다. GNN을 어떻게 설계하고 GNN의 expressive power를 어떻게하면 올릴지도 중요한 내용들이다. 이러분 부분 외에도 이번에 살펴볼 몇몇 방법들은 GNN에서의 over-squashing 문제를 해결하기 위해서 초점을 두고 있다. 약 2022년까지 사람들은 GNN의 expressive power를 올리는데 정말 많은 노력을 기울였다. 최근에 특히 이론을 주로 다루는 사람들은 over-squashing 문제에 집중하여 해결하려고 했다. 기존의 over-smoothing 문제도 중요한 문제이지만 이번에 알아볼 over-squashing 문제 또한 GNN에 있어 중요하다.

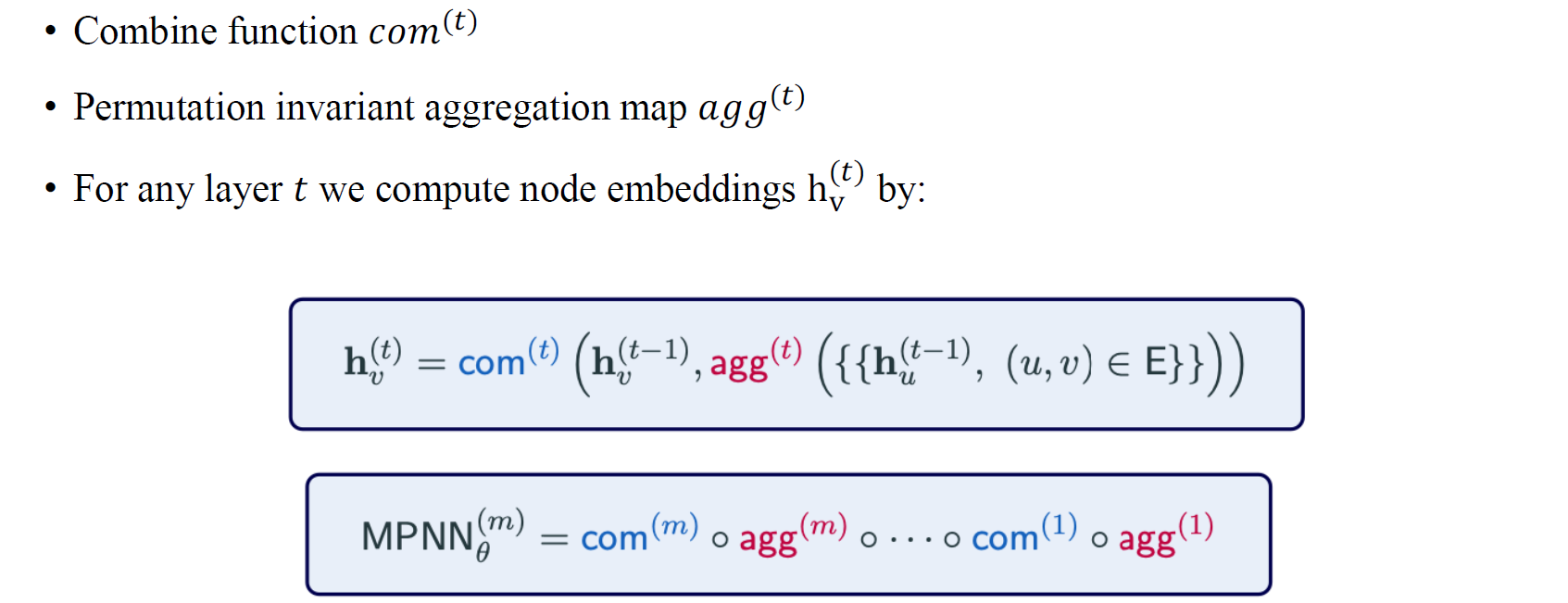
우리는 message passing neural network(MPNN)으로부터 이야기를 시작하려고 한다. 기존의 notation과 다르게 update function 대신에 이번에 우리는 combination function으로 사용하려고 한다. Message passing network를 사용하기 때문에 message passing aggregation step이 vertex들의 이웃들을 기반으로 한다는 가정이 존재한다.

Common Problems in MPNNs

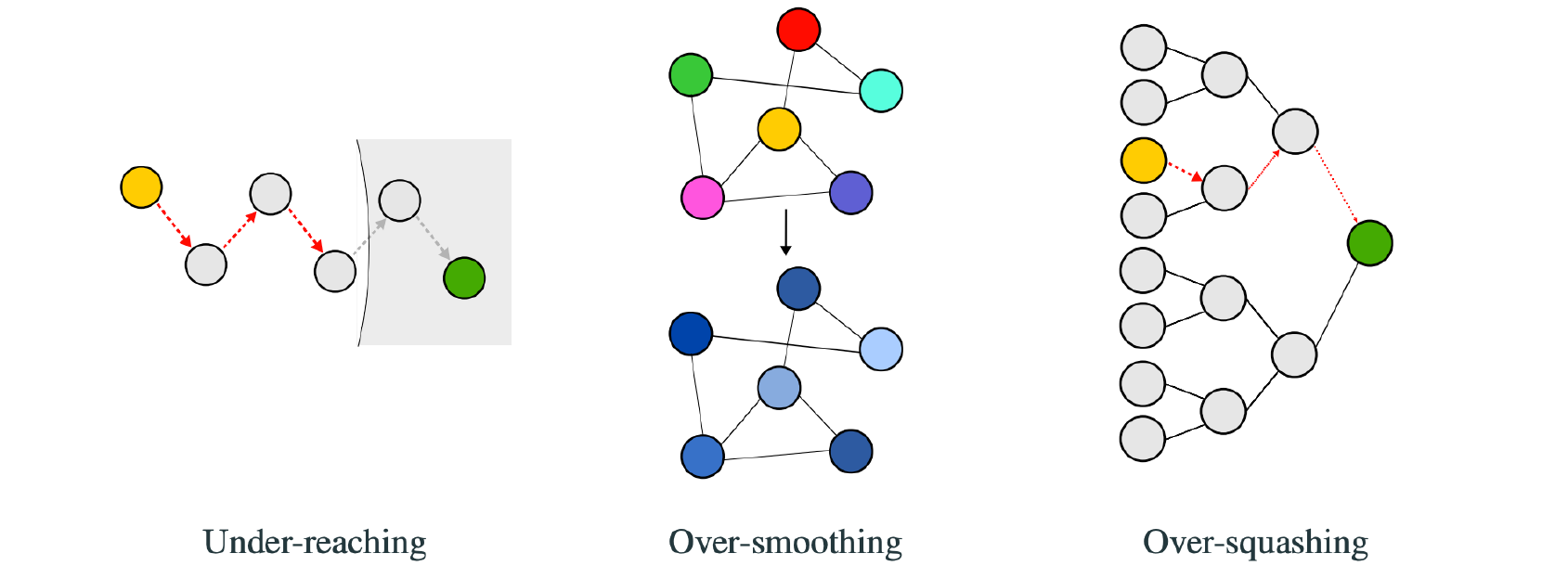우리가 MPNN에서 발생하는 문제들을 이야기할 때 물론 expressive power에 대해서 이야기해볼 수 있지만 이를 제외하고 사람들은 가장 먼저 over-smoothing 문제를 언급할 것이다. 이렇든 over-smoothing 문제도 중요하지만 under-reaching 문제와 over-squashing 문제 또한 중요한 부분이기에 차례대로 살펴보고자 한다. 하지만 over-smoothing 문제는 자세하게 이야기하지 않으려고 한다. 아무래도 over-squashing 문제 보다 사람들이 덜 형식적으로 정리해놓은면이 존재하기 때문이다. 그래서 이번에 over-squashing 문제를 자세하게 살펴보려고 하는 것이다.

Under-Reaching Problem

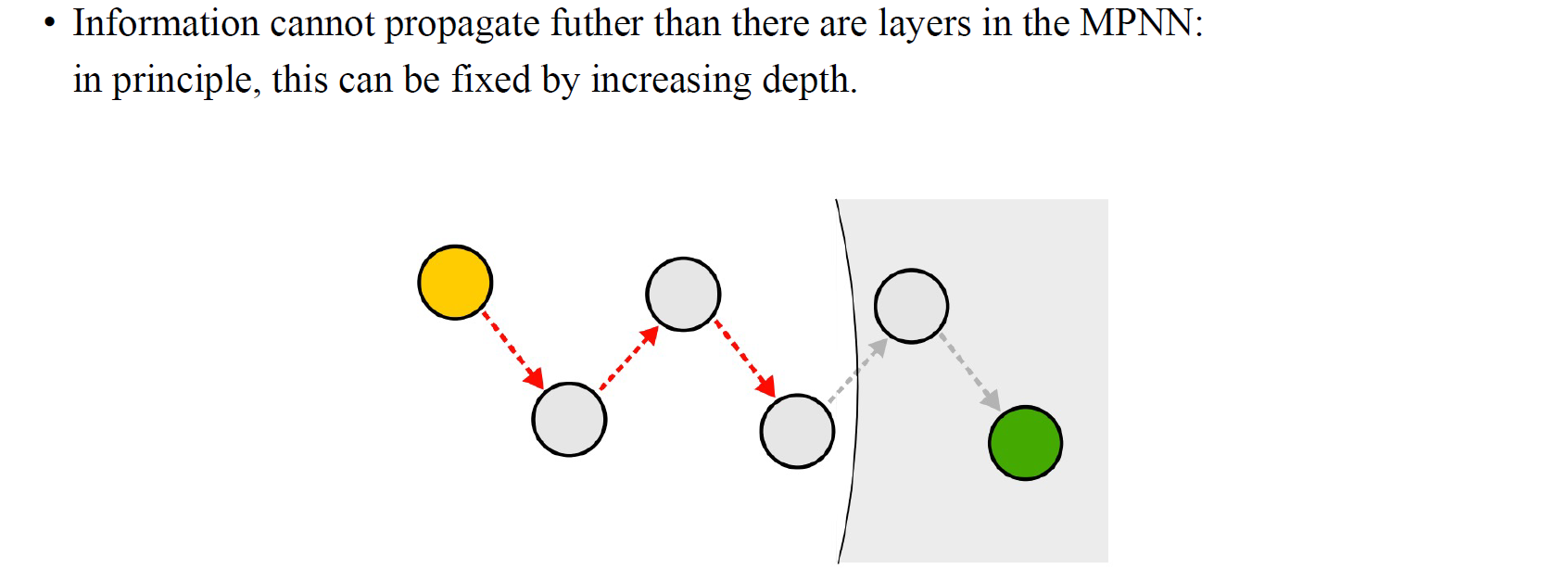가장 먼저 under-reaching 문제이고, 이는 상당히 간단한 문제이다. 특정 정보가 MPNN의 여러 layer들 중에서 어느 layer 이상으로 전달되지 않는 현상을 under-reaching이라고 한다. 여기서 우리는 위의 예시에서 노란 vertex와 초록 vertex 사이의 상호 작용에 관심을 가질 것이다. 노란 vertex와 초록 vertex 사이의 정보를 주고받기 위해서는 둘 사이에 어느정도 거리가 존재하기 때문에 GNN의 관점에서 여러 layer을 쌓을 필요가 있다. 위의 예시에서는 둘 사이에 4개의 vertex가 존재하기 때문에 GNN을 설계할 때 적어도 5개의 layer을 쌓아야 서로 정보를 주고 받을 수 있을 것이다. 물론, 더 적은 layer만으로도 가능할 수 있다. 중간 vertex 기준으로 2.5개의 layer만 있으면 노란 vertex와 초록 vertex를 상호 작용하도록 만들 수 있을지도 모른다. 하지만 이는 다른 vertex가 update된다는 기준인 것이고 실제로 노란 vertex와 초록 vertex 사이의 정보를 주고받으려면 5개의 layer는 있어야할 것이다.

Over-Smoothing Problem

Over-smoothing 문제는 GNN의 layer을 많이 쌓음으로써 발생하게 된다. Long-range 정보를 주고받기 위해서라도 GNN의 layer를 깊게 쌓는 것은 불가피하다. 하지만 그렇다고 너무 깊게 쌓다보면 GNN이나 MPNN에서는 over-smoothing 문제가 발생하게 되는 것이다. Over-smoothing 문제는 GNN layer을 여러번 지나고 나면 node representation이 서로 비슷해지는 현상을 말한다. 우리는 이를 node의 정보들이 smooth out 된다고 이야기하기도 한다. 이렇게되면 문제가 graph의 구조를 약화시키게 되면서 모두 비슷한 label이나 prediction을 하게되는 문제로 이어지게 될 것이다. 사람들은 이러한 현상을 GNN에서의 low-pass filter와 같은 동작을 한다고 이야기하기도 한다. 이러한 문제를 해결하기 위해서 사람들은 다양한 방법을 시도하곤 했다. Graph signal processing으로부터 다양한 filter를 디자인할수도 있으며, batch normalization과 같은 기법을 적용할수도 있을 것이다.

Over-Squashing Problem

Over-squasing 문제는 over-smoothing 문제보다 더 중요하고 최근들어 더욱 관심을 가지게 된 문제 중 하나이다. 위와 같이 GNN의 computational graph에서 각 message passing step에서 많은 양의 정보들이 모아지게 될 것이다. 그리고 이는 layer를 지날때마다 기하급수적으로 정보량이 많아지게 될 것이다. 위와 같이 layer를 3개 쌓고 degree가 전부 2라고 가정하기만해도 초록 vertex의 입장에서는 많은 양의 정보들을 받아들이게 된다. Degree가 2만 해도 2의 제곱으로 정보량이 많아지게 되는데, 실제로 graph에서는 이보다 많은 degree를 가지고 있는 상황이 대부분일 것이기에 상당히 많은 양의 정보를 하나의 vertex가 받아들이게 된다. GNN은 graph를 tree로서 computational graph를 만들고 long-range 정보를 받아들이는 효율적인 path를 찾아야 한다. 결국 우리는 노란 vertex에서 초록 vertex로 가는 가장 효율적인 path를 찾아서 정보를 전달하도록 만들어야 한다. 하지만 tree의 크기가 기하급수적으로 커지기 때문에 실제로 굉장히 어려운 문제에 해당한다.

간단하게 max pooling이나 sum pooling으로 문제를 해결해볼 수 있다고 생각할 수 있지만, 이러한 방법은 나머지 정보들을 상당히 버리는 형태가 되어 실질적인 해결이라고는 볼 수 없다. Comutational tree에서 max aggregation은 하나의 path를 선택하는 방법이기는 하지마 이것이 꼭 정답이 아닐 수도 있다. 단순히 이렇게 aggregation을 고정시키는 행동은 over-squashing 문제를 해결하지 못한다. Graph의 topology에 따라서 over-squashing 문제는 쉽게 해결하기 어려운 문제가 되었다. Over-squashing을 해결하는 방법들에 대해서 이번에 알아볼 것이고 대표적인 사례로 graph transformer나 graph rewiring의 방법들이 존재한다.

Understanding Over-Squashing 1

가장 먼저 ICLR 2022에 나왔던 "Understanding Over-Squashing and Bottlenecks on Graphs via Curvature"라는 논문을 통해서 어떻게 GNN의 over-squashing 문제를 해결했는지 알아보자. 저자들은 사람들이 GNN에 over-squashing 문제가 발생하고 있음을 알고 있었지만, 그동안 어떠한 이론적 해석도 없었다고 이야기한다. 이들은 sensitivity analysis를 통해서 over-squashing 현상을 정량화하고자 했다. 만약 다시 이전의 예시에서 초록 vertex가 어떠한 representation도 없다고 한다면 노란 vertex에 대해서 초록 vertex가 얼마나 sensitive한지를 이야기하고 싶었다. 이들은 또한 over-squashing 문제가 어떠한 model을 선택하는지와는 독립적으로 발생한다는 것을 증명하였으며, 이 현상은 graph 자체에 high negative curvature를 가지는 edge를 가질 때 발생한다고 주장했다. 여기서 high negative curvature라는 것은 수학적으로 다소 복잡한 개념으로, MPNN에서 정보의 bottleneck을 표현하는 방법이라고 생각하면 된다. 추가로 이들은 처음으로 rewiring method를 제안하였다. 만약 message passing 구조에서 bottleneck이 존재한다면 이는 graph의 edge에서 발생하는 것이기에 추가로 edge를 더하는 것은 bottleneck을 완화할 수 있을 것이라고 이야기했다.

Sensitivity Analysis

우선 저자들이 주장하는 sensitivity analysis를 통해서 over-squashing 현상이 해석된다는 부분을 볼 것이다. Output feature $h_v$와 input feature $h_u^0$ 사이의 interaction에 관해서 살펴본다고 해보자. 우리가 궁금한 것은 얼만큼 $h_v$가 $h_u^0$에 대해서 sensitve한지이다. Over-squashing 현상은 멀리 떨어진 vertex에 대해서 interaction을 학습할 수 없다는 것이다. 여기서 interaction이 위와 같이 수식으로 표현될 수 있으며, 위의 식은 2개의 vertex간 intercation을 수식으로 모델링할 수 있음을 말하고 있다. $r$번째 layer의 $h_v$와 input $h_u^0$간 interaction이 Jacobian norm으로 표현이 될 수 있는 것이다. 만약 이 norm 값이 크다는 것은 $h_v$가 $h_u$에 의해서 상당히 많은 영향을 받고 있다고 해석할 수 있다. 반대로 norm이 작아지면 그만큼 영향을 덜 받고 있음을 의미한다.

만약 combination function의 gradient와 message aggregation function의 gradient가 각각 $\alpha$와 $\beta$에 의해 bounded 되어 있다면, 이들간 sensitivity가 $\alpha,\beta$의 $r$ 제곱과 더불어 adjacency matrix의 $u,v$에 해당하는 element의 $r$제곱에 bounded된다는 주장을 하였다. 여기서 $A^r_{vu}$는 length $r$만큼의 $u$와 $v$ 사이의 walk를 의미하며, 이들이 강하게 연결되어 있다면 sensitivity는 클 것이고, 약하게 연결되어 있다면 sensitivity는 작아질 것이다.

Example: Binary Tree

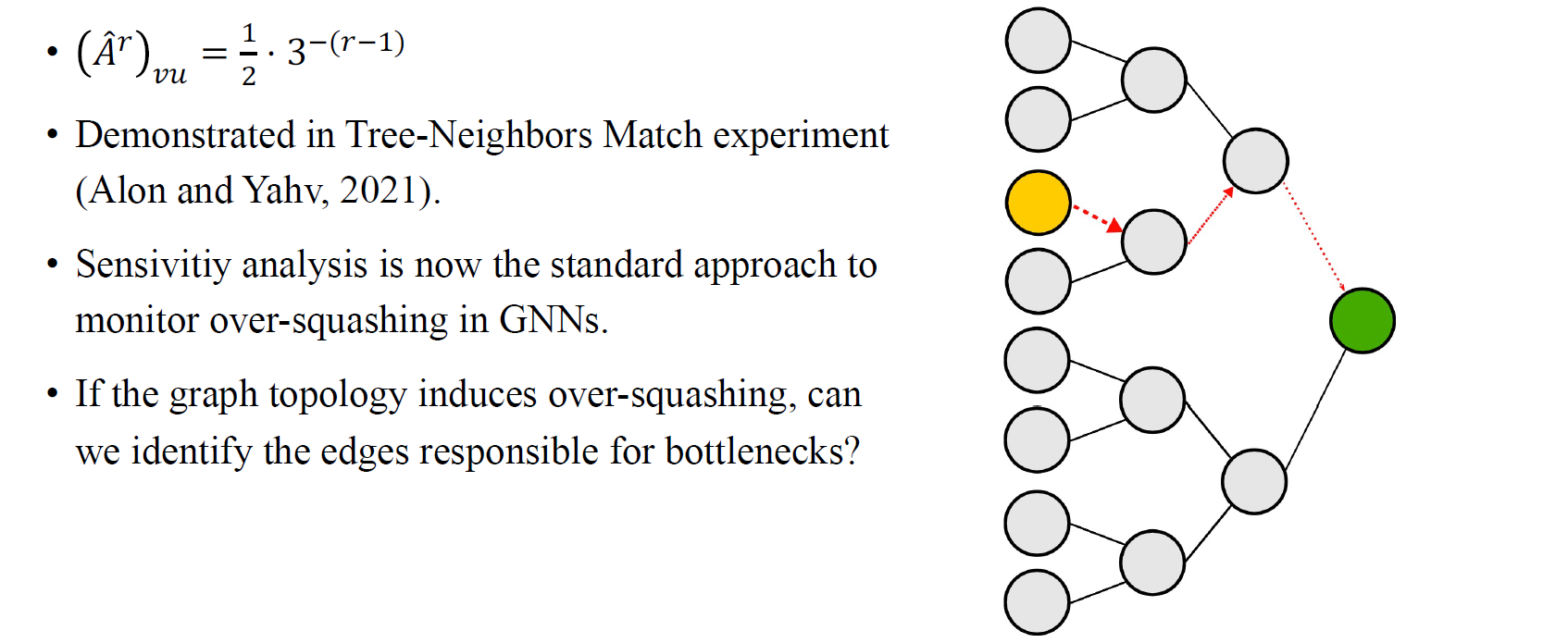이를 이해하기 위해서 간단하게 binary tree 예시로 알아보자. $A^r_{vu}$ 값이 위와 같이 $1/2\cdot3^{-(r-1)}$이고, 이는 $r$에 비례하여 값이 작아지는 것을 볼 수 있다. 각 leaf로부터 root까지의 path가 오로지 하나만 존재하는 것이 bianry tree이다. 이는 실제로 over-squashing 현상을 측정하는 유명한 실험 중 하나이다. 이 실험에서는 GNN을 사용해서 tree를 처리하면서 leaf로부터 root의 color를 검출하기를 원한다. Sensitivity analysis는 over-squashing 현상을 모니터링하기에 적합하면 지금은 표준적인 접근법 중 하나로 여겨진다. 이러한 분석은 tree에 적합하기에 이러한 식으로 정량화하는 것이 가능했다.

Edges with High Negative Curvature

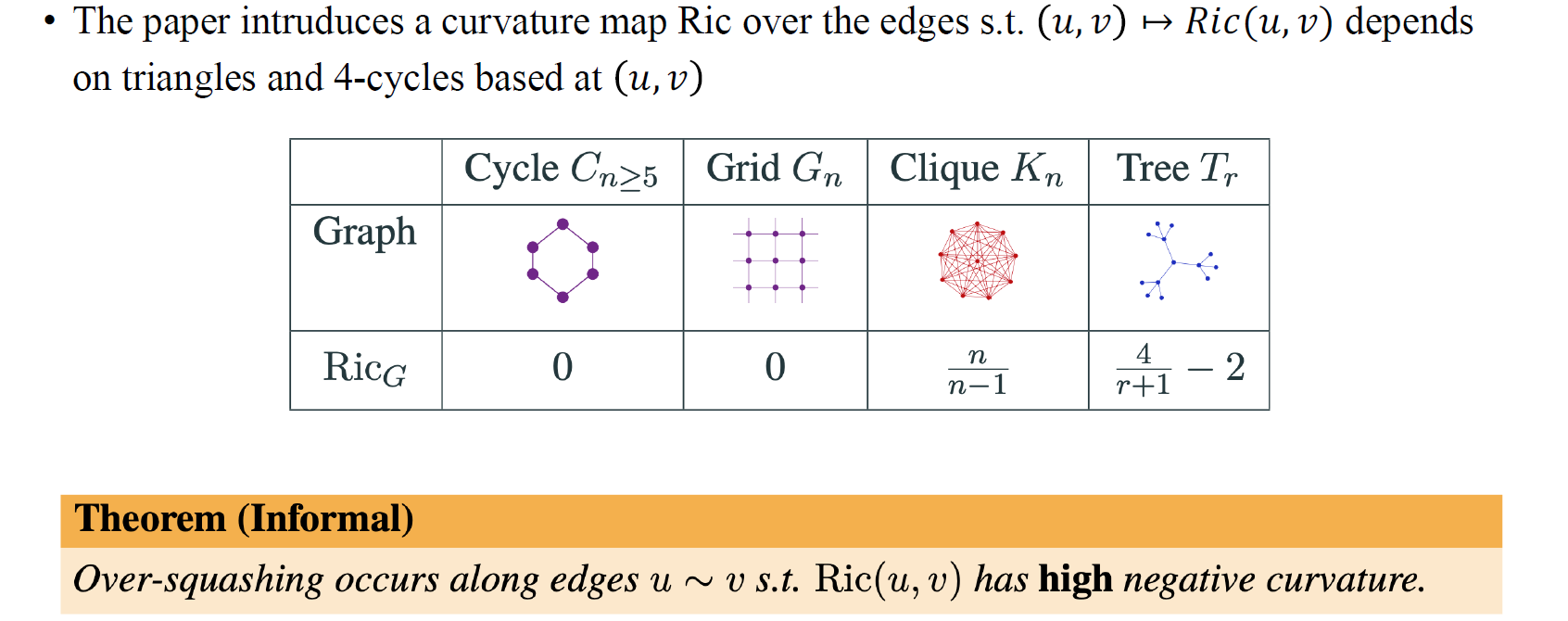이 논문에서 주요 아이디어는 high negative curvature를 가지는 edge들이 over-squashing 문제를 더 높은 확률로 유도한다는 점에서 비롯되었다. 디테일적인 부분까지 이해하려면 많은 내용과 시간이 동반되기에 간단하게 살펴보고 넘어가도록 할 것이다. Over-squashing이 특정 edge를 통해 발생한다는 것을 발견했다. 그리고 이러한 edge를 저자들은 Ricci curvature와 관련이 있다고 말한다. 이는 differential geometry와 관련된 개념으로, 만약 이 값이 -1보다 작은 아주 작은 음수인 경우에 high negative curvature를 가지는 edge에 해당하여 over-squashing을 발생시킨다고 이야기한다.

이러한 Ricci curvature는 어떠한 graph에서도 구할 수가 있으며, 대표적으로 cycle의 Ricci curvature 값을 구하면 0이 된다. Grid의 경우도 마찬가지로 0이지만, clique와 tree는 0이 아닌 값들로 구해질 수 있다. 여기서 주목할 부분은 clique로 이는 양의 범위로 curvature를 가지게 된다는 점이고, tree는 음의 범위로 curvature를 가진다는 점이다. Over-squashing 현상이 주로 tree에서 발생하는 것을 알 수 있는데, tree는 기하급수적으로 이웃이 늘어날 수 있다는 특징을 지니고 있다. 그래서 이러한 구조가 over-squashing 문제를 더욱 잘 유발하게 되는 것이다.

What is Curvature?

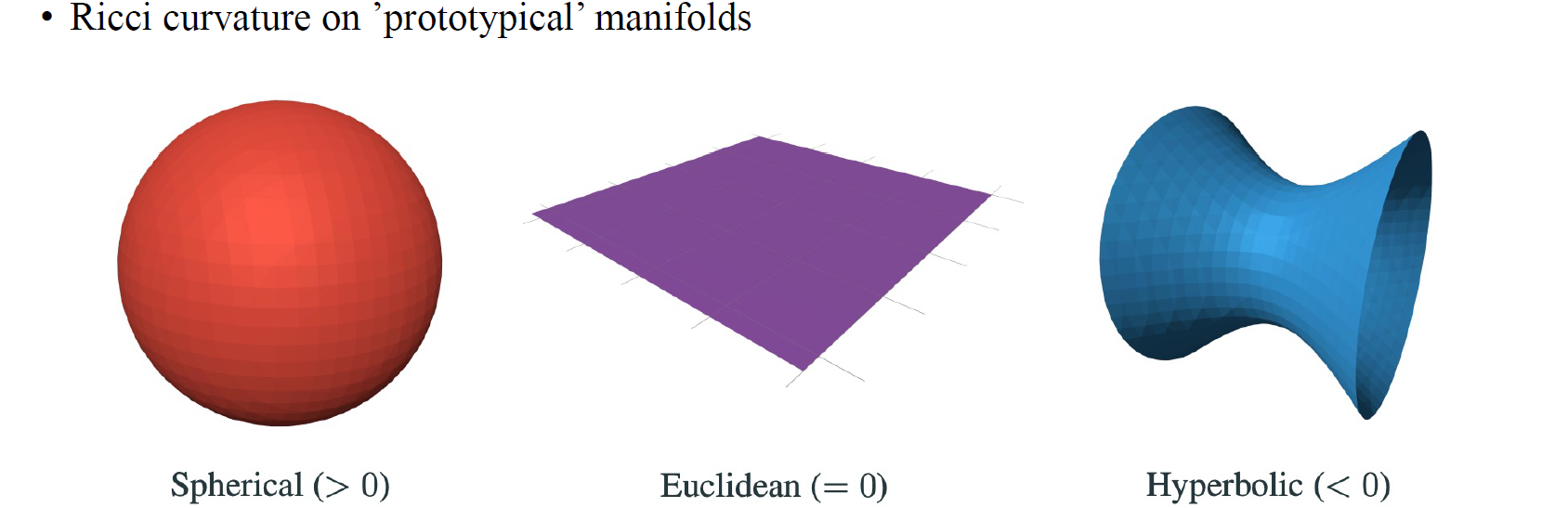Ricci curvature는 사실 Riemannian manifold을 위한 개념인데, 이를 저자들은 graph로 근사하려는 시도하였다. 이 개념은 graph의 triangle이나 cycle의 개수를 세는 개념을 기반으로 한다. 그래서 이번에는 curvature가 무엇인지 간단하게 살펴보고 이를 differential geometry의 개념과 어떻게 관련이 있는지 알아볼 것이다.

위와 같은 종류들의 curvature를 이해하기 위해서 manifold 상에서 Ricci curvature가 무엇인지를 먼저 알아보고자 한다. 이러한 개념은 사실 Riemannian manifold에서 더 정의가 되며, 우리는 Riemannian manifold를 locally Euclidean point set으로 생각할 수 있다. 이웃한 point를 몇개 선택하게 되면 이로부터 만들어지는 Euclidean plane을 찾을 수가 있는데, 이는 ball에서 존재하는 point set과 locally similar하다는 것을 의미한다.

그래서 다시 우리는 Spherical, Euclidean, Hyperbolic manifold에 대해서 알아볼 것이고, 이러한 manifold는 어떤 object를 표현하기 위해서 적절히 사용될 수 있다. 사람들은 curvature를 각 manifold에서 정의했을 때, Spherical curvature는 양수, Euclidean curvature는 0, 그리고 Hyperbolic curvature는 음수를 보여주는 것을 발견했다.

Ricci Curvature Intuition

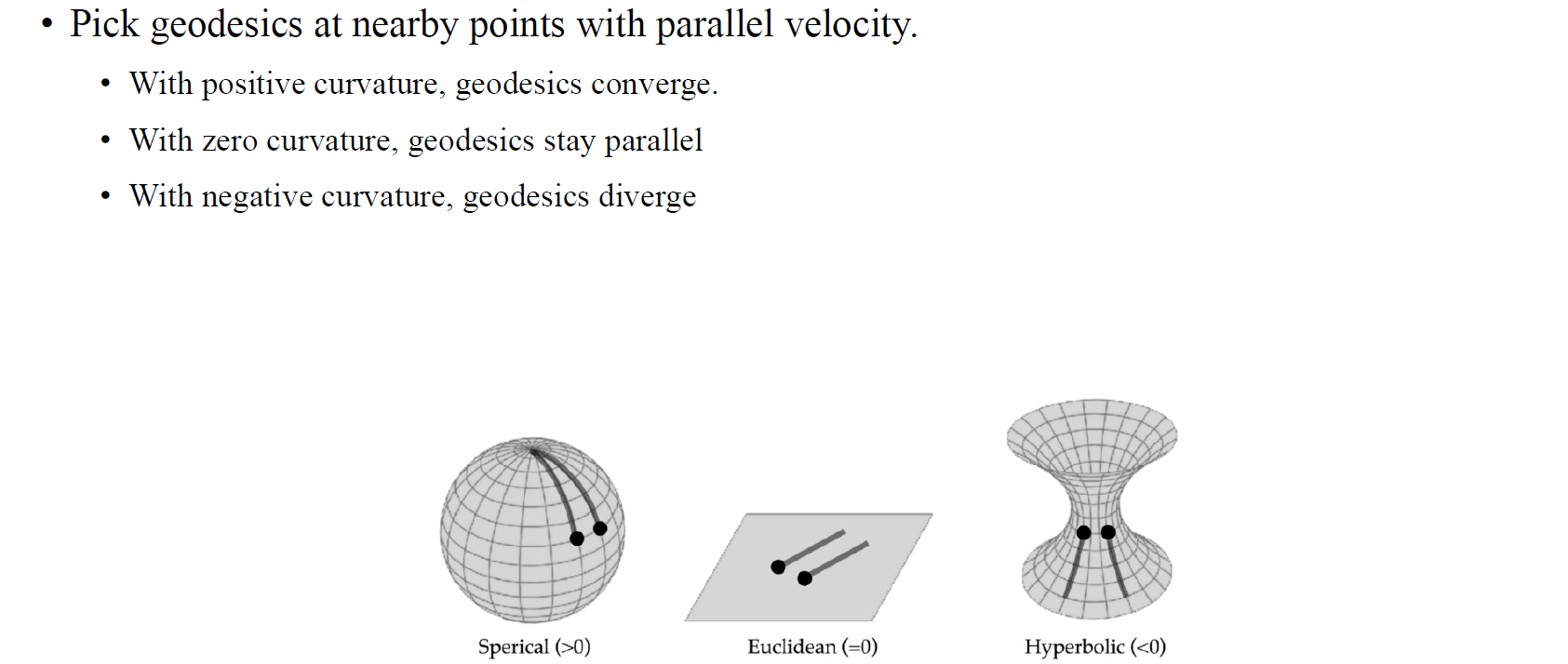Ricci curvature를 직관적으로 이해해보자. 어떤 ball에서 하나의 point를 다른 point로 움직인다는 가정하에 geodescis로 불리는 shortest path가 생기게 되고, ball의 부피가 geodescis를 따라서 증가하거나 감소한다는 사실을 알 수가 있다. 어떤 point로부터 geodesics를 그린다고 했을 때 우리가 관심있는 것은 두 geodesics가 발산하지는 아니면 수렴하는지이다. 사람들은 2개의 geodescis로부터 도착한 두개의 point의 차이나 2차 미분값에 관심을 가졌다. Spehrical의 경우에는 2개의 geodesics를 어떻게 선택하더라도 서로 수렴하게 될 것이고, Hyperbolic의 경우에는 반대로 발산하게 된다. 즉, Spherical의 경우 curvature가 양수가 되는 것이고, Hyperbolic의 경우 반대로 음수가 되는 것이다. 이렇듯 geodesics의 수렴과 발산에 따라 curvature를 정의할 수 있다.

Surgical Analysis: Graph-Rewiring

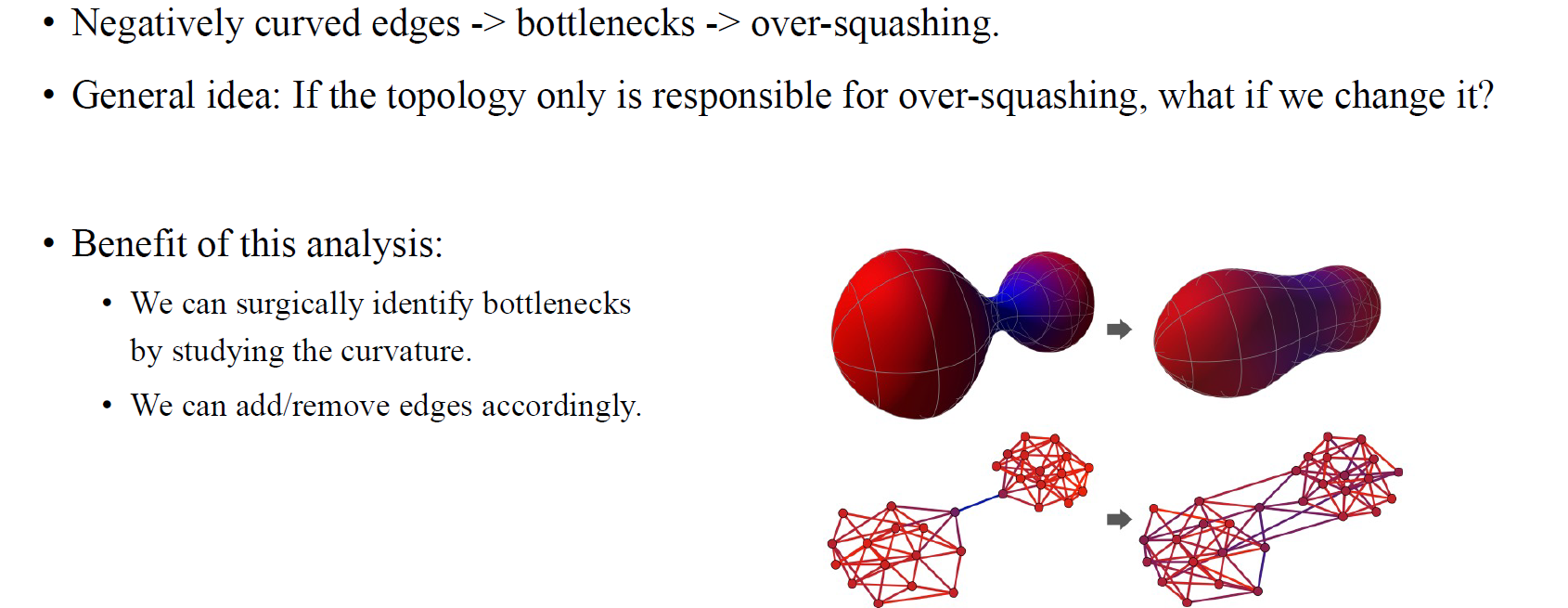그러면 이번에는 graph의 관점에서 geodesics를 생각해보자. Graph에서 geodesics는 edge를 따라 횡당하는 것과 같은 개념이다. Edge와 geodesics의 개념을 바꿔서 생각해보면 curvature를 이해할 수 있게 된다. 만약 graph 상에서 random walk를 한다고하면, 이는 되돌아오는 확률에 해당하게 될 것이다. 시작 vertex로부터 도착 vertex까지의 확률과 같으며, 이는 위에서 보았던 $A_{vu}$의 element와 관련이 있게 된다. 이러한 분석에 따르면, negatively curved edge는 over-squashing의 원인이 되는 bottleneck을 유도하게 된다. 저자들은 graph에서 잘못된 부분을 고치려는 시도를 하였고, negatively curved edge가 over-squashing을 유도하는 현상을 완화하기 위해서 edge를 추가해주었다. 위와 같이 negatively curved edge가 graph 상에서 존재하면 전반적인 curvature를 올려줄 수 있는 edge를 찾아서 추가했다. 그래서 전체적으로 graph에 우측과 같이 edge가 추가되면 curvature가 작아져 negatively curved edge의 영향력을 없애주게 된다.

Example: Graph Rewiring

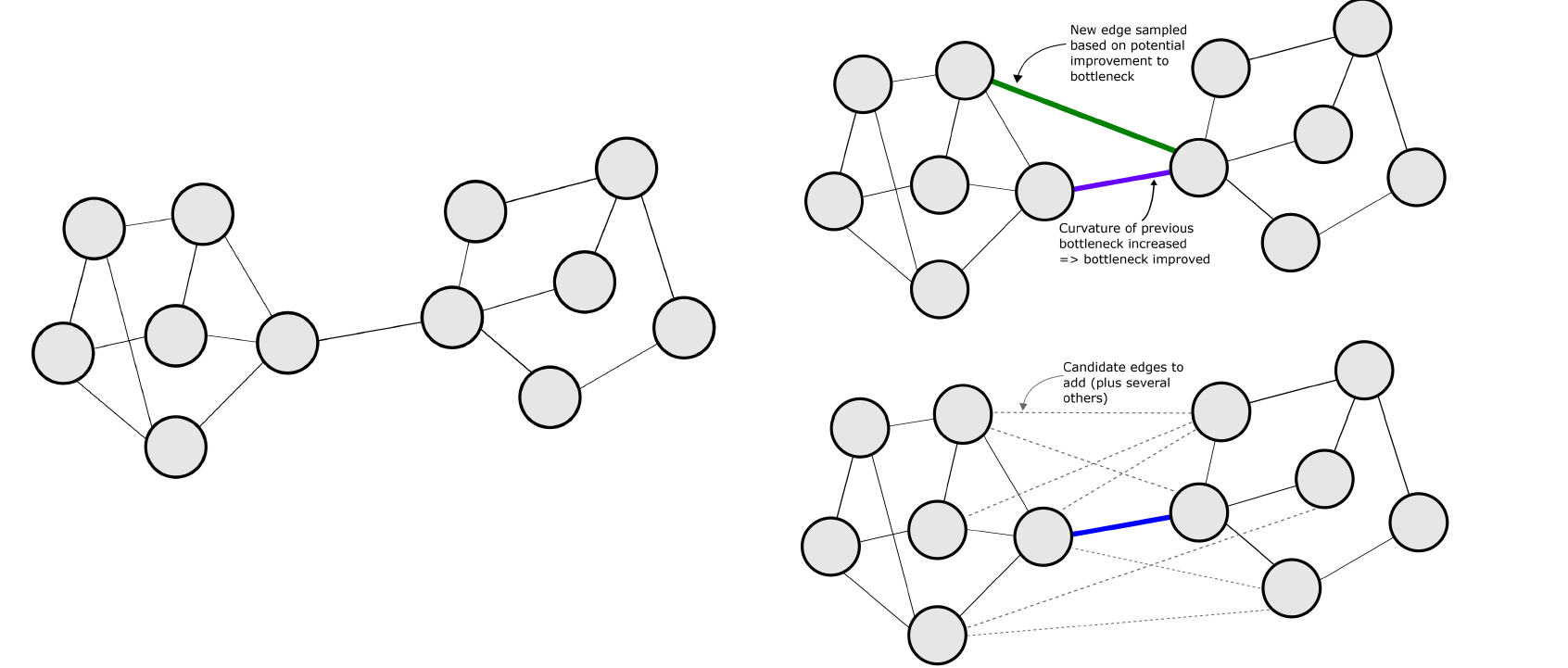예를 들어서 이들이 하고자 하는 것은 graph 상에서 전체적으로 curvature를 증가시킬 수 있는 새로운 edge를 sampling하는 것이다. 그렇게 해서 추가될 수 있는 edge들을 실제로 추가하여 graph의 curvature를 증가시켜주는 것이다.

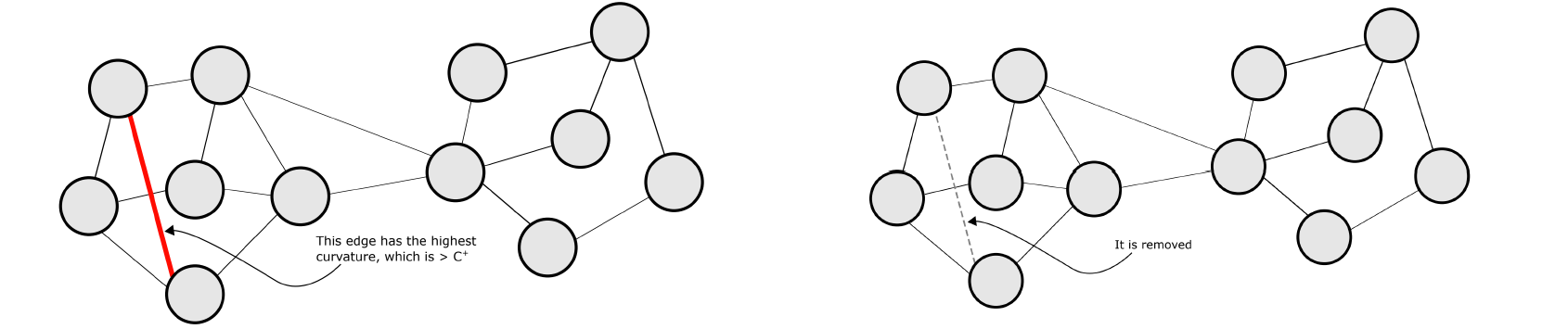또한 graph 상에 존재하는 기존의 edge들 중에서 curvature가 가장 큰 edge를 골라서 제거해주는 방법도 over-squashing 현상을 완화할 수 있다. Curvature가 가장 큰 edge는 graph의 clique로 존재할 가능성이 큰 edge이다. 결국 bottleneck을 유발할 수 있는 edge를 제거하여 over-squashing 현상을 개선하는 것도 해결책이 될 수 있는 것이다.

Understanding Over-Squashing 2

첫번째 살펴본 논문은 over-squashing 현상을 curvature를 통해서 정량화하여 분석하고 제안하는 알고리즘을 통해서 over-squashing 현상을 완화하는데에 contribution이 존재한다. 이후에 더욱 해석하기 용이한 두번째 논문 "On Over-Squashing in Message Passing Neural Network: The Impact of Width, Depth, and Topology"가 ICML 2023에 등장하였다. 첫번째 논문은 over-squashing을 분석하고 완화시키는 좋은 논문이었지만, 몇가지 질문들이 아직 남아있었다. Over-squashing을 완화시키는데 있어서 model의 width 등의 영향력이 어떠한지, over-squashing 현상이 충분히 깊은 model들에 의해서 완화될 수 있는지 등의 다양한 관점의 질문들이 아직 해결되지 못했었다. 이번에 살펴볼 논문을 통해서 첫번째 논문과 다른 관점에서 over-squashing 현상을 분석하고 이해해볼 것이며, 특히 message passing neural network의 구조를 주목해서 볼 필요가 있다.

Setting

이 논문은 결국 GNN의 width를 증가시켜주게 되면 over-squashing 현상이 완화될 수 있음을 주장했다. 이는 꽤 직관적이다. GNN의 width가 증가하면 결국 GNN이 저장할 수 있는 양도 함께 늘어나기 때문이다.

Impact of Width

앞서 over-squashing을 sensitivity를 통해서 정량화할 수 있음을 이야기했다. 이 논문에서도 마찬가지로 두 vertex간 영향력을 gradient norm을 이용해서 bound하였고, 이들의 크기를 통해서 서로의 영향력을 정량화하였다. 다만, 기존과 다른 부분은 GNN의 width의 영향력을 분석하기 위해서 network의 residual term이나 aggregation term의 coefficient로 sensitivity를 bound시킨 것을 볼 수 있다. 결국 MPNN과 같은 GNN의 width, depth, topology 정보를 기반으로 vertex 사이의 영향력을 정량화 시켰고, 이를 통해서 over-squashing 문제를 완화시키고자 시도했다.

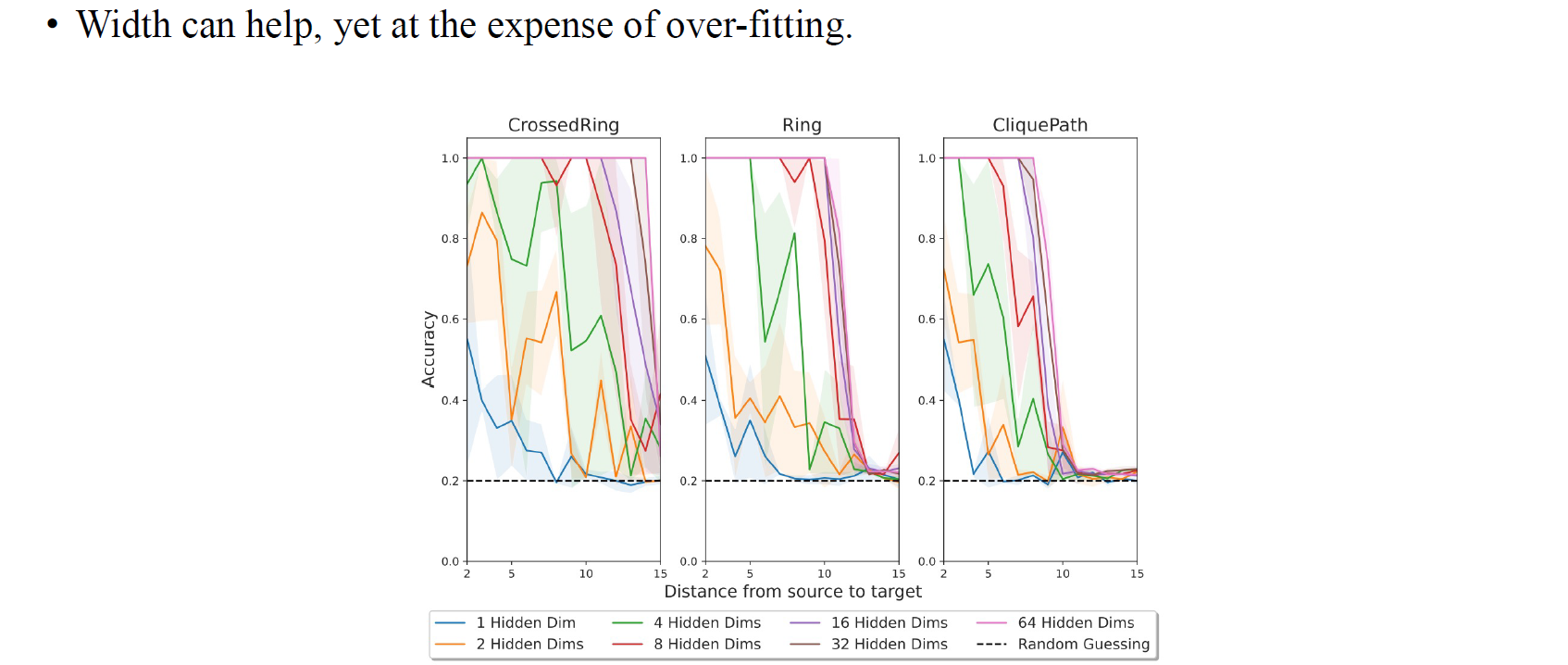저자들은 over-squashing이 일어날 수 있는 환경을 만들어서 실험을 통해서 증명했다. 더욱 어려운 환경 속에서 network의 hidden dimension을 늘려가면서 실험을 통해 문제를 풀고자했다. GNN의 width의 영향력을 보기 위한 이러한 실험 세팅은 꽤 흥미로운 부분이라고 할 수 있다.

What Does It Mean 'Long-Range'?

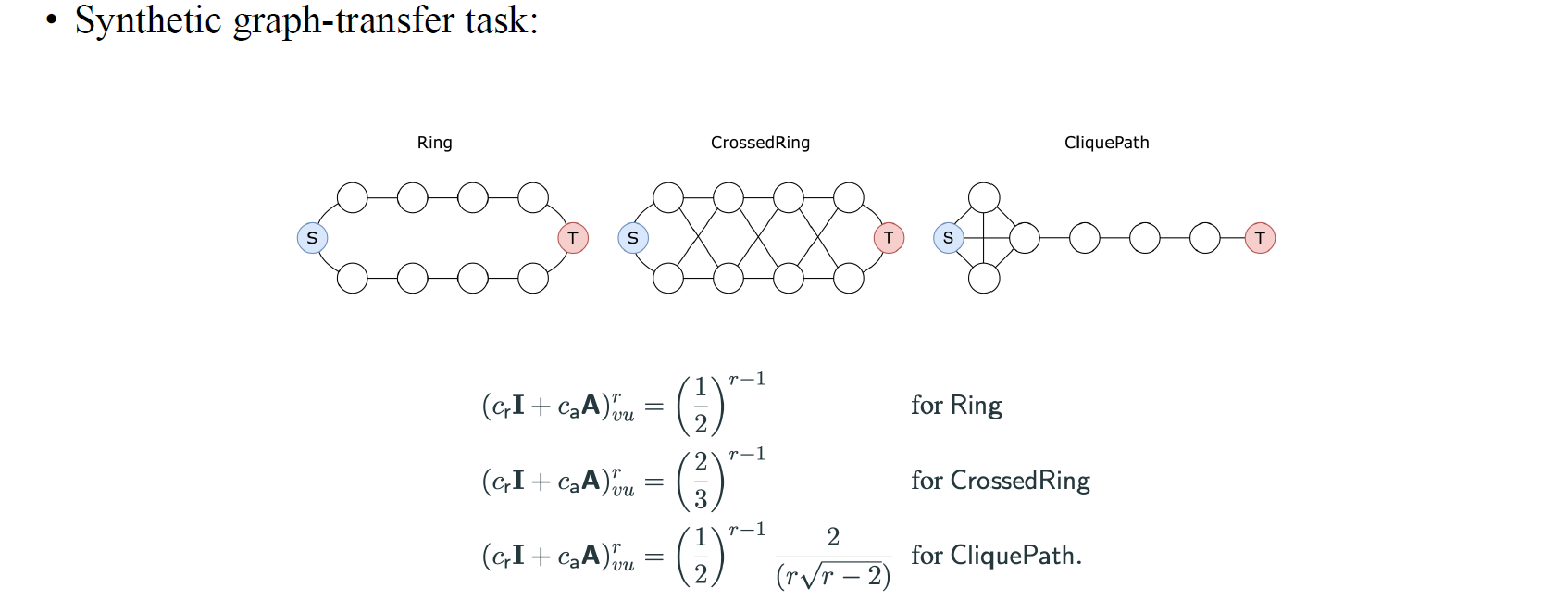이들은 source vertex S와 target vertex T 사이의 interaction에 관심을 가졌고, ring, crossedring, cliquepath라는 이름으로 graph transfer task를 만들어 sensitivity의 우변의 값들을 각기 다르게 얻을 수 있었다.

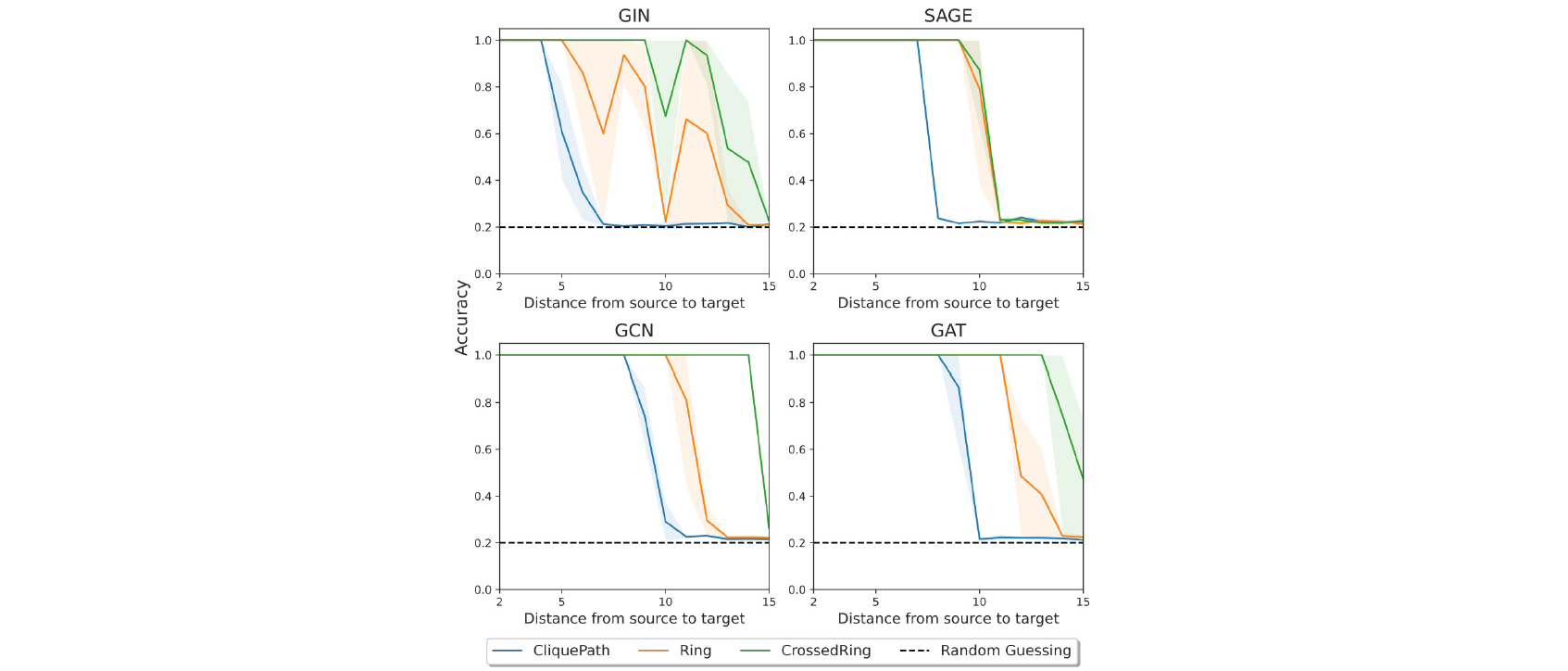그리고 source vertex와 target vertex 사이의 거리를 늘리게 되면 GNN의 성능이 저하되는 것은 실험적으로 증명했다.

Random Walk

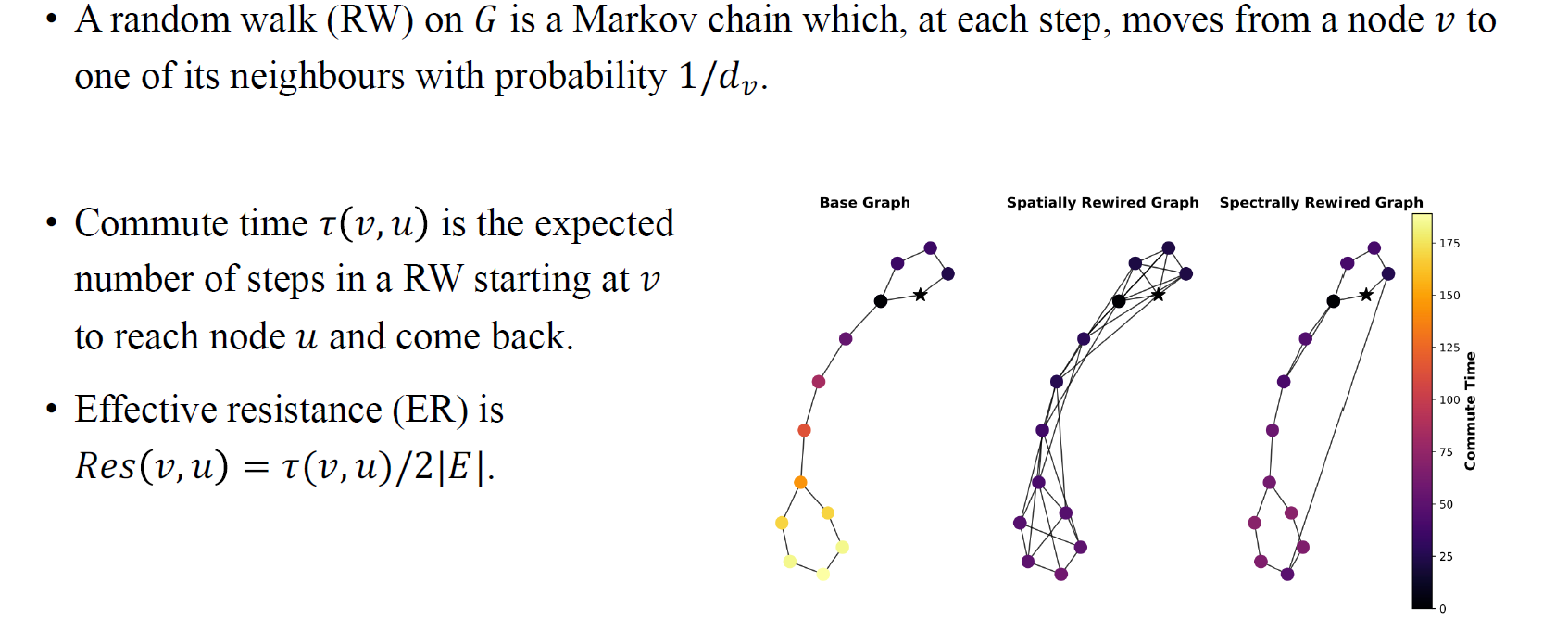저자들은 또한 random walk를 기반으로 하는 이론을 제시하였다. Message는 graph가 주어졌을 때 random walk를 수행하는 것이라고 이야기했다. 저자들은 node $v$에서 이웃한 node들로 일정한 확률 $1/d_v$로 이동하는 특정 random walk를 고려하였다. 그리고 over-squashing을 commute time에 관해서 분석하였다. Commute time은 node $v$에서부터 $u$로 갔다가 되돌아오는 random walk에서 예상되는 step의 수를 의미한다. 위의 예시에서는 별로 표기된 node에서 노란 node로 갔다가 다시 별 모양의 node로 돌아오는 step 수를 나타낼 것이다.

만약 tail vertex에서 출발하여 clique에 들어가게 된다면 빠져나오지 못할 가능성이 크다. 이러한 경우에는 commute time이 굉장히 커질 것이다. 그래서 graph connectivity를 개선하여 over-squashing을 완화하는 rewiring을 가이드해주기 위해서 effective resistance가 정의되었다.

Over-Squashing and Commute Time

만약 commute time이 굉장히 크다면 over-squashing 현상을 해결하기 어렵다. 그래서 저자들이 결국 말하고자 하는 것은 highly negative curvature edge라는 것이 수학적으로 어려운 개념이자 도구이기 때문에 vertex 쌍으로부터 effective resistance를 구해서 graph rewiring을 쉽게 시도할 수 있다는 것이다. 결론적으로 저자들은 over-squashing 현상에 있어서 GNN의 width, depth와 더불어 graph의 topology가 중요한 역할을 한다는 것을 발견하였으며, width의 영향력을 통해서 이 현상을 어느정도 완화할 수 있음을 실험적으로 보여주었다. Graph의 topology 정보의 경우 commute time이 이러한 현상을 발생시킬지와 관련한 중요한 정보라는 것을 발견하였으며, commute time에 비례하여 over-squashing 현상이 심해진다는 것을 이야기했다.