Weighted interval scheduling은 n개의 일이 주어지고 각각의 일을 j라고 할 때, s_j에서 시작해서 f_j에 끝나며 v_j의 weight를 가지고 있다. 여기서 모든 weight가 1인 경우에는 interval scheduling 문제로 greedy algorithm으로 해결하면 된다. 하지만 weight가 존재하는 경우에는 dynamic programming으로 해결해야 한다. 우리가 여기서 하고 싶은 일은 겹치지 않는 선에서 weight의 합을 최대로 만들고 싶다. 다음의 예시를 보자.
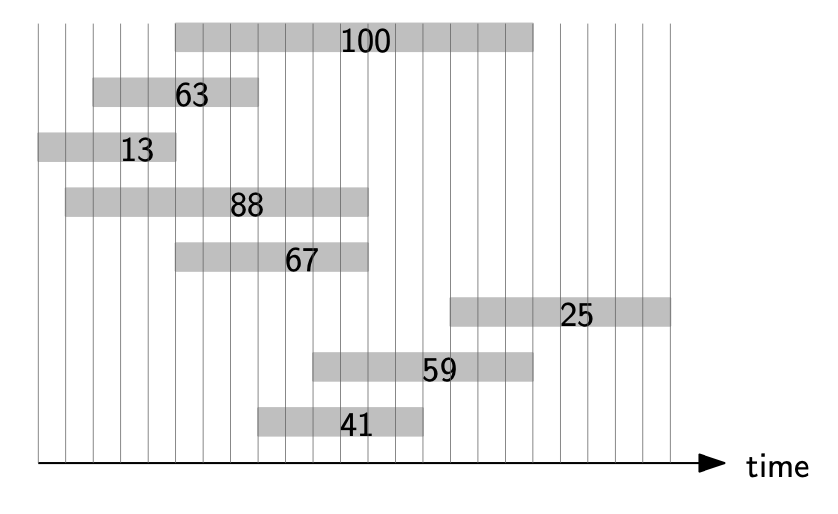Greedy하게 100부터 고른다고 생각해보자. 그러면 다음으로 13을 고르게 되면 weight의 합이 113이 된다. 다른 경우로 13부터 고른다고 생각했을 때, 다음으로 67을 고르게 되고, 마지막으로 25를 고르게 되어 weight의 합이 105가 된다. 그렇기 때문에 시작 시간을 기준으로 하든지, weight가 큰 기준으로 하든지간에 greedy하게 접근하는 것은 다른 반례를 만들어낼 수가 있어서 weight가 존재하는 경우에는 dynamic programming으로 해결해야 한다. 우선 알고리즘은 다음과 같다.
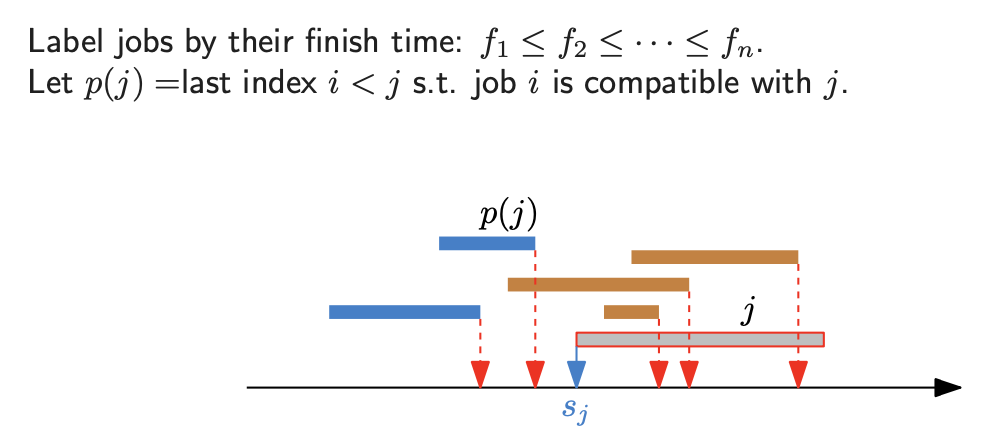
우선 끝나는 시간을 기준으로 정렬하는 과정이 필요하다. 그리고 j라는 일을 선택한 경우와 선택하지 않은 경우에 대해서 큰 경우를 택하면서 최적의 해를 찾으면 된다. 그리고 i번째 일이 j번째 일보다 먼저 일어났을 경우, i와 j가 compatible 하다는 이야기는 f_i가 s_j보다 작거나 같아야 한다.
