트리의 개요

트리는 정점(Node)과 선분(Branch, 가지)을 이용하여 사이클을 이루지 않도록 구성한 그래프의 특수한 형태이다.

• 트리는 하나의 기억 공간을 노드라고 하며, 노드와 노드를 연결하는 선을 링크(Link)라고 한다.
• 트리는 가족의 계보(족보), 조직도 등을 표현하기에 적합하다.

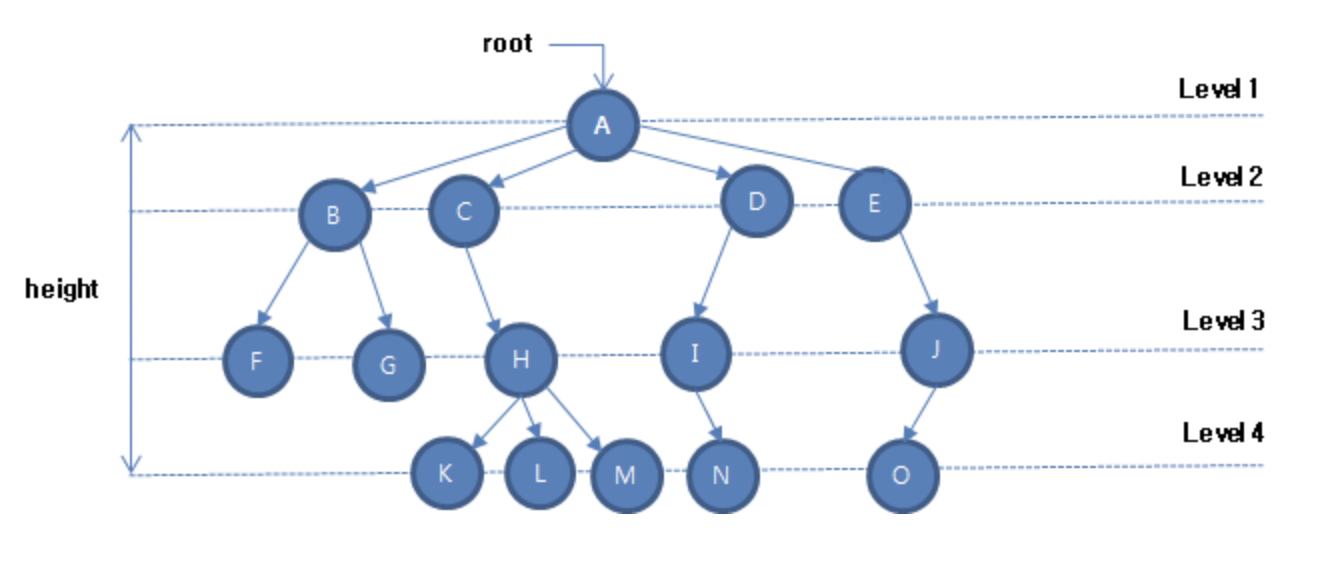
• 노드(Node): 트리의 기본 요소로서 자료 항목과 다른 항목에 대한 가지(Branch)를 합친 것
• 근 노드(Root Node): 트리의 맨 위에 있는 노드
• 디그리(Degree, 차수): 각 노드에서 뻗어 나온 가지의 수
• 단말 노드(Terminal Node) = 잎 노드(Leaf Node): 자식이 하나도 없는 노드, 즉 디그리가 0인 노드
• 자식 노드(Son Node): 어떤 노드에 연결된 다음 레벨의 노드들
• 부모 노드(Parent Node): 어떤 노드에 연결된 이전 레벨의 노드들
• 형제 노드(Brother Node, Sibiling): 동일한 부모를 갖는 노드들
• 트리의 디그리: 노드들의 디그리 중에서 가장 많은 수

트리의 운행법

트리를 구성하는 각 노드들을 찾아가는 방법을 운행법(Traversal)이라 한다.

• 이진 트리를 운행하는 방법은 산술식의 표기법과 연관성을 갖는다.
• 이진 트리의 운행법은 다음 세 가지가 있다.
  
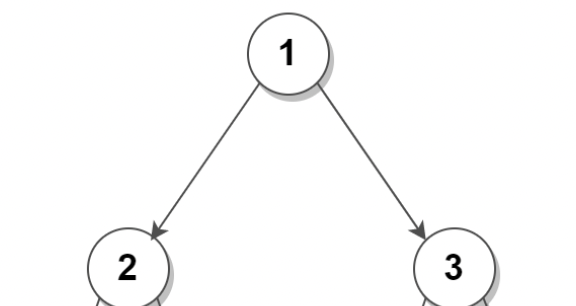
• Pre(앞)order: Root -> Left -> Right 순으로 운행 1, 2, 3
• In(안)order: Left -> Root -> Right 순으로 운행 2, 1, 3
• Post(뒤)order: Left -> Right -> Root 순으로 운행 2, 3, 1

수식의 표기법

산술식을 계산하기 위해 기억공간에 기억시키는 방법으로 이진 트리를 많이 사용한다. 이진 트리로 만들어진 수식을 인오더, 프리오더, 포스트오더로 운행하면 각각 중위(Infix), 전위(Prefix), 후위(Postfix) 표기법이 된다.

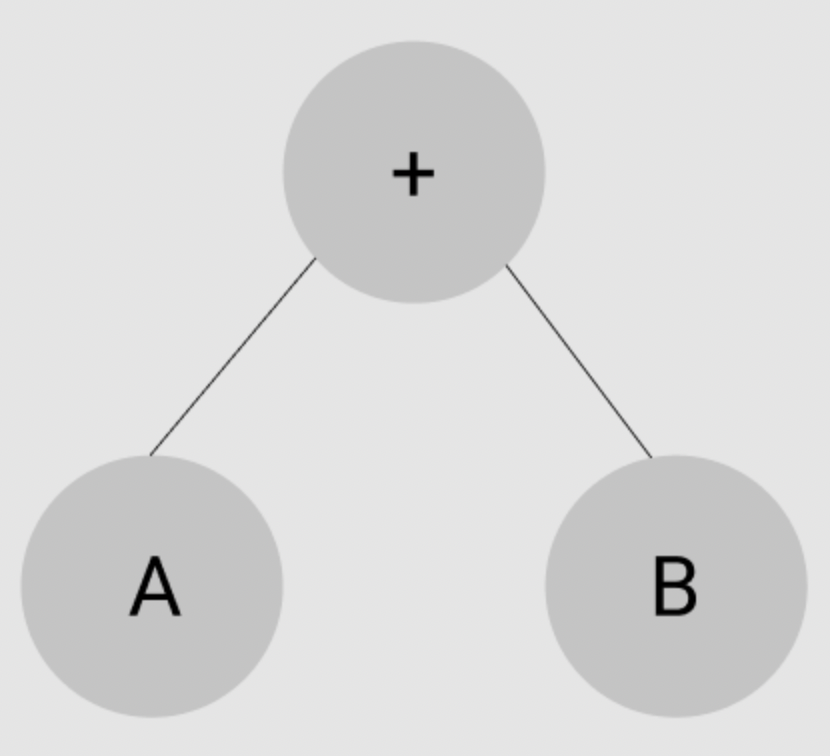
• 전위 표기법(Prefix): 연산자 -> Left -> Right +AB
• 중위 표기법(Infix): Left -> 연산자 -> Right A+B
• 후위 표기법(Postfix): Left -> Right -> 연산자 AB+

Infix 표기를 Postfix나 Prefix로 바꾸기

• Postfix나 Prefix는 스택을 이용하여 처리하므로 Infix는 Postfix나 Prefix로 바꾸어 처리한다.

다음과 같이 Infix로 표기된 수식을 Prefix와 Postfix로 변환하시오,
X = A/B * (C+D) + E

• Prefix로 변환하기

1. 연산 우선순위에 따라 괄호로 묶는다.
   (X = (((A/B) * (C+D)) + E))
2. 연산자를 해당 괄호의 앞(왼쪽)으로 옮긴다.
   =(X +(*(/(AB) +(CD)) E))
3. 필요없는 괄호를 제거한다.
   =X +*/AB +CD E

• Postfix로 변환하기

1. 연산 우선순위에 따라 괄호로 묶는다.
   (X = (((A/B) * (C+D)) + E))
2. 연산자를 해당 괄호의 뒤(오른쪽)로 옮긴다.
   (X (((AB)/ (CD)+)* E)+)=
3. 필요없는 괄호를 제거한다.
   X AB/ CD+* E+=

Postfix나 Prefix로 표기된 수식을 Infix로 바꾸기

다음과 같이 Postfix로 표기된 수식을 Infix로 변환하시오.
A B C - / D E F + * +

• Postfix는 Infix 표기법에서 연산자를 해당 피연산자 두 개의 뒤로 이동한 것이므로 연산자를 다시 해당 피연산자 두 개의 가운데로 옮기면 된다.

1. 먼저 인접한 피연산자 두 개와 오른쪽의 연산자를 괄호로 묶는다.
   ((A (B C -) /) (D (E F +) *) +)
2. 연산자를 해당 피연산자의 가운데로 이동시킨다.
   ((A /(B - C)) +(D *(E + F)) )
3. 필요없는 괄호를 제거한다.
   A /(B - C) +D *(E + F)

다음과 같이 Prefix로 표기된 수식을 Infix로 변환하시오.

• / A - B C * D + E F

• Prefix는 Infix 표기법에서 연산자를 해당 피연산자 두 개의 앞으로 이동한 것이므로 연산자를 다시 해당 피연산자 두 개의 가운데로 옮기면 된다.

1. 먼저 인접한 피연산자 두 개와 왼쪽의 연산자를 괄호로 묶는다.
   (+ (/ A (- B C)) (* D (+ E F)))
2. 연산자를 해당 피연산자 사이로 이동시킨다.
   ( ( A /(B - C)) +(D *(E + F)))
3. 필요없는 괄호를 제거한다.
   A /(B - C) +D *(E + F)