[DSP]#1 Spectrogram

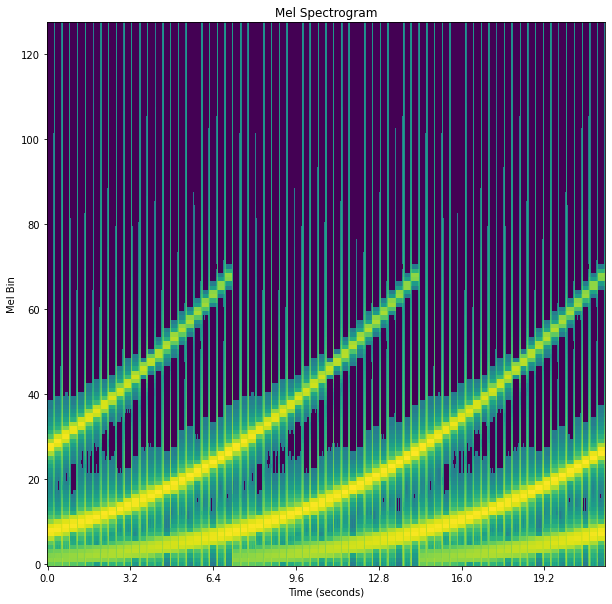
정다샘 교수님의 MIR강의 중 1st assignment에 관한 내용을 정리한 문서입니다.
해답 코드는 첨부하지 않고, 숙제 과정에서 제가 알게된 내용들을 위주로 기록 해보았습니다.

https://github.com/jdasam/ant5015-2023

자세한 내용은 위 링크에서 찾아보시길 바랍니다.

Digital Sound Processing

midi pitch vs frequency

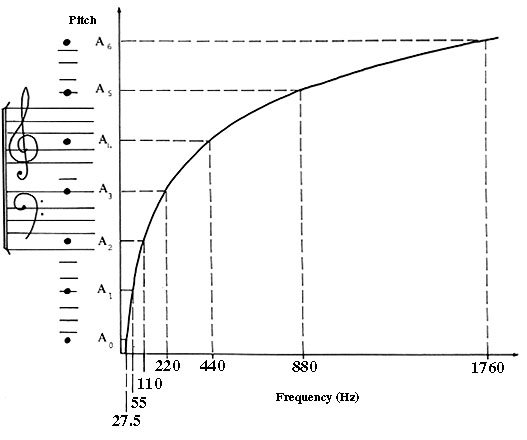
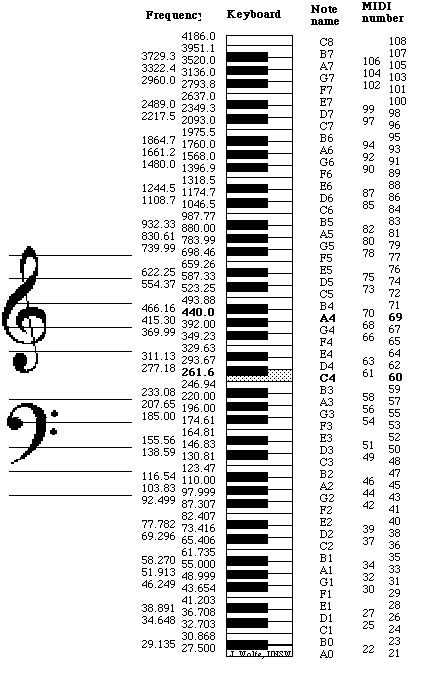
• Hz를 Pitch로 변환하는 식 (평균율 기준)
  • $f(h) = \log_2(\frac{h}{440}) \times 12 + 69$
  • h: Hz
• MIDI Pitch를 Hz로 변환하는 식 (평균율 기준)
  • $f(\text{p})= 440 \times 2^{\frac{p-69}{12}}$
  • p: MIDI Pitch
  • f(p): MIDI Pitch에 해당하는 Hz
  • p=69일 때 f(p)=440Hz이며, p가 1늘어날 때마다 주파수가 $\times 2^{\frac{1}{12}}$ 비율로 증가함

as 1 midi increase, then 2 ** (1/12) frequency increase
and 2 ** (1/12) is bigger than 1 so a frequency is getting larger.

sine wave

처음 sine 파형을 그리려고 하면 헷갈리는게 sin 함수 안에 무엇을 넣어주여야하는 가이다.
torch.sin은 반지름이 1인 원을 기준으로 계산하기에 인풋이 2 pi면 한바퀴의 호의 값을 의미한다.

radian = torch.arange(0, 2*pi, 0.01)
torch.sin(radian)
plt.plot(radian, torch.sin(radian))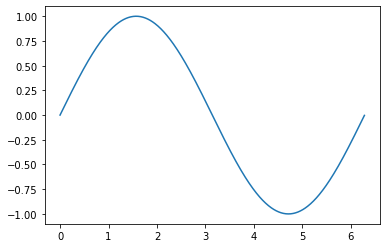

그러니까 우리는 원하는 샘플의 위치에 어떤 sin 값이 나오면 되는 지를 생가하면 된다.
hz가 1인 sine wave의 경우에는 0번째 샘플은 0에서 시작해서 sample rate의 값에 해당하는 샘플에서 큰 웨이브가 하나 만들어져야 한다.
그렇다면 time_frame /sr 에다가 frequency를 곱해주면 x축인 time_frame들은 frequency로 더욱 증폭된 sine 값들과 매칭되게 된다.

it is important to know the formula for a sine wave:

y(t) = A * sin(2 * pi * f * t)

where:

y(t) is the amplitude of the sine wave at time t
A is the amplitude or maximum value of the sine wave
f is the frequency of the sine wave in Hertz
t is the time in seconds

frequency : 440Hz, sampling rate : 16000
sine_wave의 500개까지의 샘플을 그려본 모습

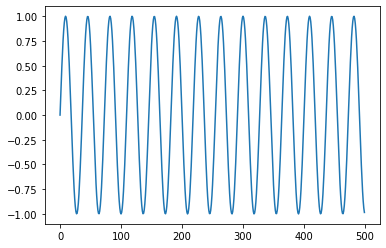
the reason why using radian

https://m.blog.naver.com/alwaysneoi/100188370054

# Radians incorporate the notion of arc length or distance into their definition.
# The measure of an angle in radians is based on the length of the corresponding arc on a unit circle.
# In contrast to angles, which are purely a measure of rotation, radians represent both an angle and a distance traveled along a circular path.

multi pitch

이거는 아이디어가 간단하다.
그냥 각각의 sine wave를 더해주면 된다.

순정률just intonation & 평균율equal temperament

• 음고가 2배가 되면 같은 음으로 인지되는 것을 옥타브라고 한다.
  • 한 옥타브 안에 있는 음표들 끼리 어떤 음고 비율을 가지게 만들까?
• 순정률은 각각의 음고 (Hz) 관계가 정수배로 표현되는 조율법 의미한다.
  • 정수배 비율로 표현된다는 것은 유리수, 즉 분모와 분자가 정수인 분수로 표현할 수 있다는 말이다.
  • 순정 8도는 근음과 높은음의 음고 비율이 1:2가 되는 관계다.
  • 순정 5도는 근음과 높은음의 음고 비율이 2:3이 되는 관계다
  • 순정 장3도는 근음과 높은음의 음고 비율이 4:5가 되는 관계다.
  • 순정 단3도는 근음과 높은음의 음고 비율이 5:6이 되는 관계다.
• 평균율은 한 옥타브를 12개의 반음으로 쪼개고 각각의 반음 간의 음고 비율이 모두 일정하게 만든다.
  • 반음 끼리의 주파수 비율은 $2^{\frac{1}{12}}$
  • 화음을 만들때 음끼리 정확한 정수배가 되지 않는다

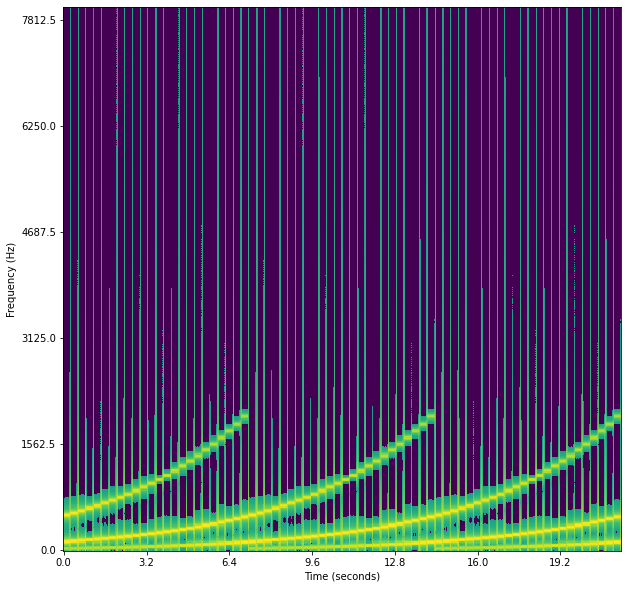
Spectrogram

torch.fft.fft

torch.fft.fft는 입력한 샘플의 개수와 같은 frequency의 샘플을 뱉어낸다.
하지만 이중에서 반은 허수부complex number이므로 없애주어야 한다.
이 함수의 정확한 작동원리를 알지는 못하지만 적어도 이 함수는 nyquist theorum을 만족한다는 것을 알 수 있다.

dft = torch.fft.fft(shepard_audio[0:400])
print(dft.shape)
plt.plot(dft)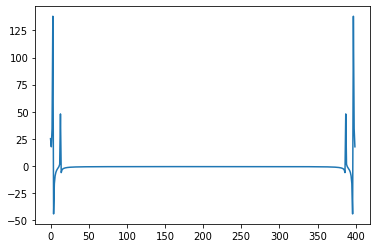

torch.fft.fft() is a function in PyTorch that computes the one-dimensional discrete Fourier Transform (DFT) of a real or complex tensor using the Fast Fourier Transform (FFT) algorithm.

The DFT is a way to transform a signal from the time domain to the frequency domain, which means it decomposes a signal into its component frequencies. The FFT algorithm is a fast way to compute the DFT, and it is used extensively in signal processing and other applications where the frequency content of a signal is important.

In PyTorch, torch.fft.fft() takes a tensor as input and returns its DFT as a tensor of the same shape. The input tensor can be either real or complex, and the output tensor will be complex. The output tensor will have the same shape as the input tensor, except for the last dimension which will be truncated to (n_fft//2 + 1) to eliminate redundancy.

Calculating frame numbers

이 부분이 처음에 헷갈릴 수 있다. 어떤 길이Total를 그 보다 작은 어떤 길이size로 나눠주는 것은 size에 해당하는 프레임이 total에 몇개가 들어가는 지와 같다. 이게 나눗셈의 몫의 개념 중에 하나이다.
그렇다면 이 프레임이 hop_size 만큼 떨어져 겹쳐서 나열되어 있다면 이 프레임이 total에 몇개가 들어가는 지 어떻게 알 수 있을까?
아래의 그림을 참조하자.

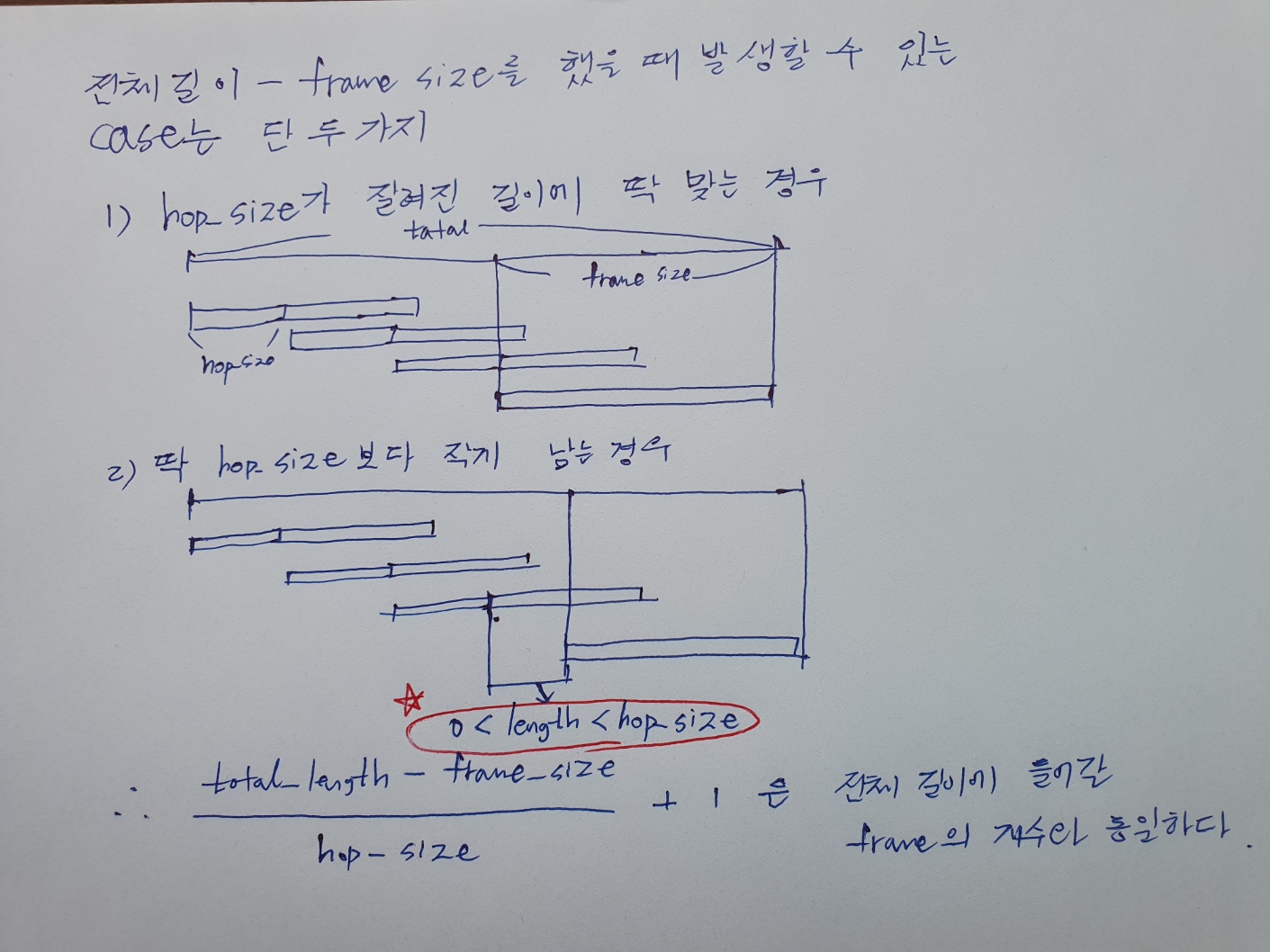
Changeability of frames

축의 값을 변환해보자.

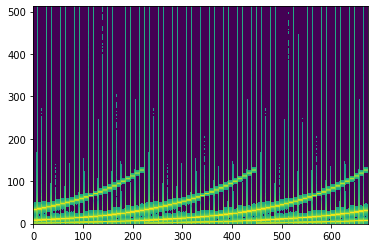
frequency_bin_to_hz

상호 변환은 조금 까다롭다. 가령 frequency는 nyquist theorm에 따라 sampling rate의 절반에 해당하는 최대값을 가질 수 있다. 하지만 torch.fft.fft를 사용하면 우리가 보게 되는 것은 n_fft에 해당하는 bin의 frequency이다. 즉 우리가 400개의 샘플만을 잘라본다면, 8000Hz의 값은 200개의 bin을 가지게 되는 것이다. 그래서 window의 사이즈가 커질수록 frequency의 해상도는 높아진다.(trade-off로 time의 해상도가 낮아진다.)

because bin_index is self.n_fft//2+1, we can use self.sr/self.n_fft to get frequency(self.sr / 2)

time_bin_to_second

같은 원리로 time_bin은 len(audio) // hop_size로 생각할 수 있다. 그리고 초는 len(audio) // sampling_rate이다.

because bin_index is len(audio) / hop_size, we can use hop_size / sr to get second(len(audio) / self.sr)

hz_to_mel

어떤 양수의 값을 log에 넣어준다는 것은 간단하게 생각하면 초기값의 변화를 나중의 변화보다도 더 큰 변화로 생각하겠다는 것이다.

amplitude_to_DB

https://en.wikipedia.org/wiki/Decibel#Field_quantities

DB 값은 상대값이기에 reference power 값이 필요하다.
이 비율값인 파워에 10log10을 취해주면 된다.
하지만 만약에 그 안의 값이 이미 power라면 그냥 10log10을 해주면 된다.

power

If the spectrogram is in power (squared) values, taking the logarithm will convert it to a decibel (dB) scale.