기수 정렬 (Radix Sort)

기수정렬의 개념

기수 정렬이란?
기수 정렬이란 자릿수를 기준으로 정렬 하는 알고리즘으로,
값들간에 비교연산을 하지않고 정렬할 수 있는 안정적인 정렬 알고리즘의 일부이다.


안정적인 정렬 알고리즘?
=> 두 개의 원소가 같은 값일 때, 둘 사이의 기존의 정렬 순서가 유지되는 정렬을 말한다.

ex) 예를 들어 key값이 다른 두 개의 원소가 5의 값을 가진다고 가정하자, 이럴 때 정렬 된 뒤에도 key값에 따라 선행되어있던 5가 이후에도 선행되어 있다면 안정적인 정렬 알고리즘이다.

기수 정렬의 특징

1. 빠른 속도
기수 정렬은 인자들을 비교하지 않고 자릿수를 기준으로 한다는 점에서
빠른 정렬속도를 가지게 됩니다.

2. 안정정렬
또한 안정정렬이므로 기존에 정렬된 자릿수의 값이 같은 경우,
정렬이 바뀌지 않고 기존의 순서를 유지하게 되므로 원하는 정렬을 이룰 수 있습니다.

3. 추가 메모리
하지만 "제자리-정렬"이 아니기 때문에 데이터를 보관하기 위해
추가적인 메모리를 필요로 합니다.

기수 정렬 이해를 돕겠습니다.

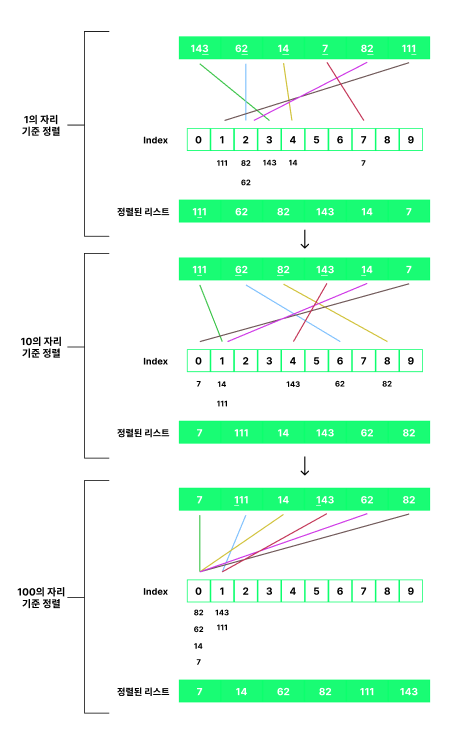
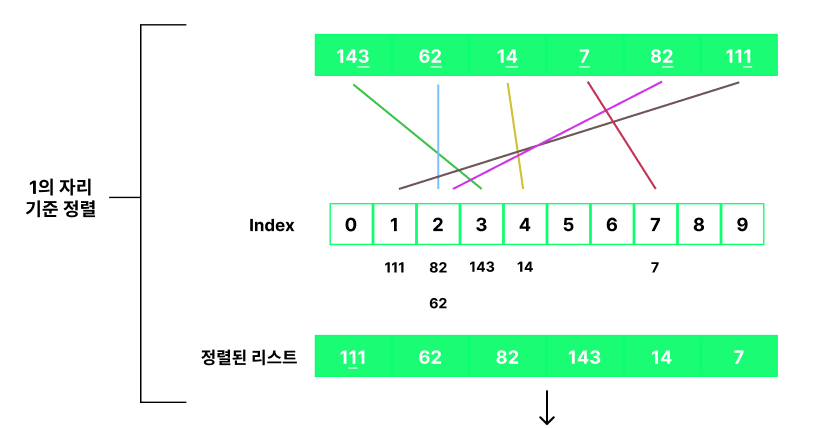
1의 자리수를 기준으로 정렬을 먼저 진행합니다.
아래의 사진을 참고해보면 각각의 숫자를 인덱스에 맞게 배치합니다.
전부 배치가 끝나면 0~9 인덱스를 돌면서 들어온 순서대로 뽑아서 (선입선출)
하나의 배열을 완성합니다.

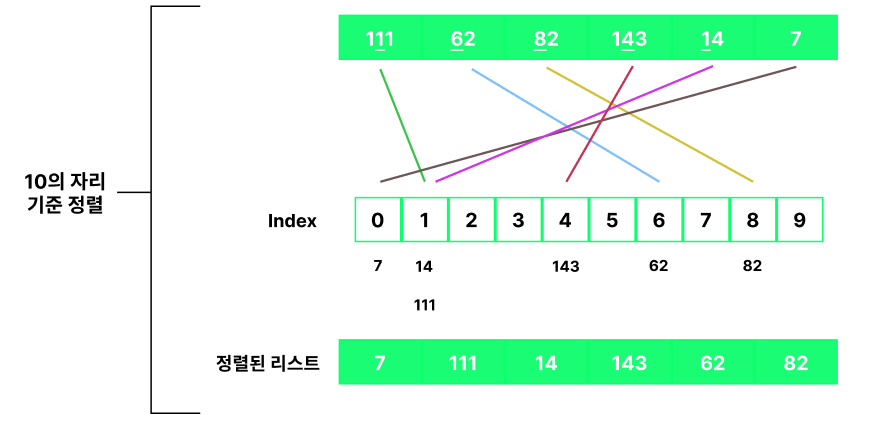
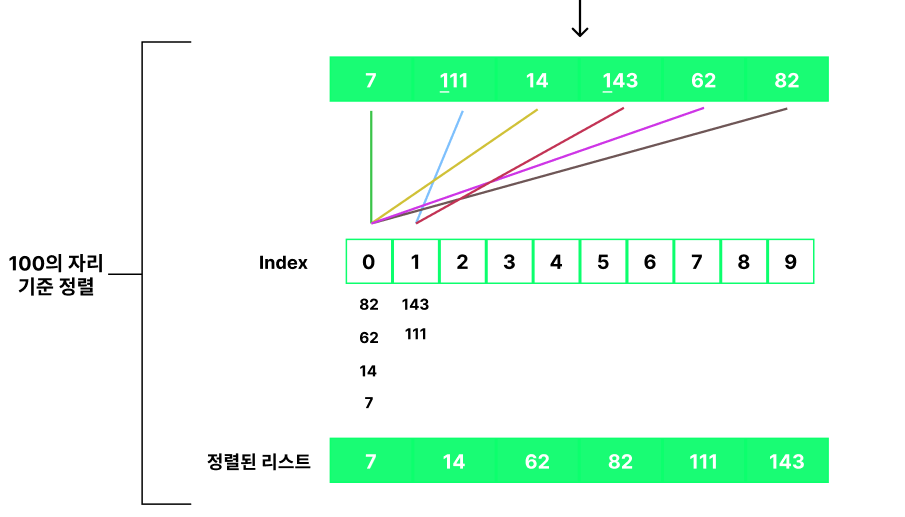
그리고 위의 과정을 최대값 ( => 143 )의 자릿수까지 반복하게 됩니다.
즉, 100의 자릿수까지 기준으로 정렬하게 되는것입니다.

기수정렬 Java 코드

- 해당코드는 Queue를 사용하여 정렬을 진행하였습니다.

import java.util.Arrays;
import java.util.Queue;
import java.util.LinkedList;

public class Main{
    public static void main(String[] args){
    	int[] testArray = {143, 62, 14, 7, 82, 111}; 
        
        System.out.println("정렬 전 : "+ Arrays.toString(testArray));
        radixSort(testArray);
        System.out.println("정렬 후 : "+ Arrays.toString(testArray));
        
    }
    
    public static void radixSort(int[] arr){
        // 자리수를 지정할 Radix변수와 , 최대자릿수를 가리킬 최대값을 구합니다.
        final int MaxNumber = getMaxNum(arr);
        int radix = 1, ArraySize = arr.length;
        
        // bucket 초기화
        Queue<Integer> bucket = new LinkedList[10];
        for (int i = 0; i < 10; i++){
        	bucket[i] = new LinkedList<>();
        }
        
        // 자릿수별로 순차적으로 정렬 - (LSD : 최하위 자리수 정렬)
        while (radix <= MaxNumber) {
        	// bucket에 담기
        	for (int idx = 0; idx < ArraySize; idx++){
            	bucket[(arr[idx] / radix) % 10].add(arr[idx]);
            }
            
            // bucket에서 꺼내기
            for (int arr_idx = 0, bucket_idx = 0; bucket_idx < 10; bucket_idx++){
            
            	// 해당 bucket Index Queue안에 데이터가 들어있는 경우이기에 꺼냅니다.
            	while (!bucket[bucket_idx].isEmpty()){
                	arr[arr_idx++] = bucket[bucket_idx].poll();
                }
            }
            
            // 한 번의 자릿수를 기준으로 정렬했으면 다음 자릿수로 넘어가기
            radix *= 10;
        }
        
    }
    
    // 최대자릿수를 알아낼 수 있게, 배열에서 가장 큰 수 구하기
    public static int getMaxNum(int[] array){
    	int maxNumber = array[0];
        for (int indexNumber : array){
        	if (indexNumber > maxNumber)
            	maxNumber = indexNumber;
        }
        return maxNumber;
    }
}

기수정렬을 마무리 하며

기수정렬을 하는데에는 LSD , MSD 정렬방식으로도 나뉘며
기수정렬과 카운팅 정렬의 결합(Radix sort with Counting Sort)을 이용하면
더 좋은 최적화 정렬방법을 얻기도 한답니다.

기수정렬은 숫자들간에 비교연산을 진행하지 않고 새로운 공간을 두고
배치되는 위치에 따라 정렬이 진행됩니다.
이는 기존의 비교연산을 진행하여 정렬하는 방법과는 다른 점이라 새롭고 신기하기도 하지만
메모리가 너무 커지지는 않을까 걱정이 되기도 합니다.

하지만 부담되지 않을 메모리를 사용할 것이라고 판단한다면 그 만큼 빠르기에 매력적으로 다가옵니다.

기수정렬을 배움으로 인해 당연시 숫자들간에
비교를 해야한다는 고정관념을 부술 수 있어서 좋았고,
참신한 방법에 생각의 견해가 넓어진 것 같아 다들 한 번쯤 배우기 좋은 이론이라고 생각합니다.