Partial FFT의 사용 목적

FFT 알고리즘은 효율적으로 DFT를 수행하는 알고리즘으로 매우 광범위한 분야에서 활용되고 있다. FFT의 출력 샘플 크기는 알고리즘적으로 입력 샘플 크기와 같거나 큰 $2^n$으로 결정된다. 그러나 많은 어플리케이션에서 전체 스펙트럼 보다는 일부 스펙트럼의 신호만 관찰하고 싶은 경우가 있을 수 있다.

이런 경우에는 DFT matrix의 일부 혹은 모든 계수 값을 미리 메모리에 저장해 놓았다가 필요할 때마다 연산에 필요한 계수 값들을 불러와 사용하는 방법을 생각해볼 수 있다. 내가 관찰하고자 하는 스펙트럼의 주파수 범위가 극히 제한적인 경우에는 이런 방법을 사용하는데 크게 무리가 없다. 그러나 상황에 따라 내가 관찰하고자 하는 주파수 대역이 가변적으로 변하는 경우에는 DFT matrix 내 모든 계수 값을 메모리에 저장하여야 하는데 이는 매우 비효율적이며 때로는 불가능할 수 도 있다.

예를 들어, FFT 입력 샘플의 크기가 $N=1024$인 경우, DFT matrix의 크기는 $1024 \times 1024$이며, 각 계수 값은 complex number 이므로 I/Q 계수 값 각각을 4바이트로 저장할 경우의 필요한 메모리 공간은 $1024 \times 1024 \times 4 \times 2 = 8$MBytes이다. 8메가 바이트가 작게 느껴질 수도 있지만 환경에 따라 저장 자체가 불가능 한 경우도 있으며, 저장이 가능하더라도 크기가 크기 때문에 많은 임베디드 환경에서는 L3 RAM에나 저장이 가능하다. 그러나 L3 RAM은 메모리 접근 속도가 느리기 때문에 프로세싱 속도가 심각하게 떨어질 수 있다.

그렇다면 메모리 효율적으로 Partial FFT를 사용해가며 내가 원하는 스펙트럼만 가변적으로 관찰할 수 있는 방법은 없을까?

DFT 행렬과 구조

FFT는 DFT 연산을 효율적으로 수행한다. 그리고 길이가 $N$인 DFT 입력 벡터를 $\mathbf{x}$라 하고, DFT 출력벡터를 $\mathbf{y}$로 나타내면, DFT 연산은 그 정의에 의해 vector-matrix form으로 다음과 같이 나타낼 수 있다.

여기서 $\mathbf{W}$는 DFT matrix를 의미하며 다음과 같다. (위키참고)

여기서

위 식을 통해 DFT matrix $\mathbf{W}$의 $k$번째 행과 $n$번째 열에 위차한 성분 $\mathbf{W}(k,n)$는 다음과 같이 나타낼 수 있음을 알 수 있다.

장황하게 적어 놓았지만 사실 DFT 정의에 의해 당연한 결과이다. 복소지수 함수는 단위원 상에서 회전한다. 따라서, 만약 $nk = pN+q$의 관계가 성립하는 경우 다음과 같이 식을 전개할 수 있다. (이때, $0\leq q \leq N-1$)

우리는 위 식으로부터 다음이 결론을 도출할 수 있다.

DFT Matrix 내 모든 계수 값은 DFT Matrix의 첫 번째 행 또는 열로 나타낼 수 있다.

더 적은 수의 계수 값들만 사용하기

앞에서 우리는 $N \times N$ 크기의 DFT matrix가 포함하는 $N^2$개의 모든 계수 값을 $N$ 개의 계수 값으로 표현할 수 있음을 살펴보았다. 그렇다면 $N$개의 계수를 모두 메모리에 저장해 놓아야 할까? 식 (4)를 더 자세히 살펴보자. 식 (4)에서 $0\leq q \leq N-1$이며, $N$을 다음과 같이 두 정수 $N_1$과 $N_2$의 곱으로 생각해볼 수 있다.

이때, 보통은 $N$이 2의 거듭제곱이므로 $N_1$과 $N_2$역시 2의 거듭제곱으로 표현되는 것이 일반적이다. 그렇다고 반드시 2의 거듭제곱을 만족할 필요는 없다. $N$을 두 정수의 곱으로 표현하였으니 식 (4)에서의 $q$도 아래와 같이 등가적으로 나타낼 수 있다.

여기서 $0 \leq n_1 \leq N_1-1$이고, $0 \leq n_2 \leq N_2-1$이다. 식 (5)-(6)을 식 (4)에 대입하여 다시 정리하면 다음과 같다.

식 (7)로부터 우리는 식 (4)로 표현되는 $N$개의 계수 값들을 두 개의 지수함수의 곱으로 나타낼 수 있음을 알 수 있다. 이는 곧 $N$개의 계수 값들을 모두 저장할 필요 없이 $N_1+N_2$개의 계수 값들만을 메모리에 저장해두면 DFT matrix의 모든 $N^2$개의 계수를 표현할 수 있음을 의미한다. 물론, 앞에서와 같은 분해과정을 더 수행하면 저장할 계수 값들을 더 줄일 수 있을 것이다. 그러나 이 단계에서 더 계수 값을 줄인다한들 메모리 절감 효과는 미미한데 반해 코드의 가독성은 급격하게 떨어지게 된다.

식 (7)의 결과로부터 우리가 메모리에 저장하여야 하는 계수들은 다음과 같다는 결론을 도출 할 수 있다.

앞에서 살펴본 바와 같이 크기 $N \times N$의 DFT matrix 계수 값을 모두 메모리에 저장하려면 $8$MBytes의 메모리가 필요하였다. 반면, $N=N_1N_2 \rightarrow 1024=32 \times 32$이므로 $64$개의 계수 값만을 저장하면 DFT matrix 내 모든 계수를 표현할 수 있으며, 이때 필요한 메모리는 $64 \times 2 \times 4 = 512$bytes에 불과하다. 여기서 2와 4가 곱해지는 이유는 real과 imaginary value를 4바이트로 저장한다고 가정하였기 때문이다. 즉, $N=1024$일 때, DFT matrix 계수 값을 모두 저장하는 것보다 메모리를 $0.0061$%만 사용하여 동일한 연산이 가능해지게 된다.

DFT matrix의 크기가 $N \times N$일 때, DFT matrix의 첫 번째 행 또는 열의 모든 계수는 $N_1 + N_2$개 계수의 곱으로 나타낼 수 있다. 여기서 $N=N_1N_2$이다.

간략화가 가능했던 이유

앞에서 살펴본 내용들은 수학적으로 명확하다. 그렇다면 물리적으로는 어째서 이러한 해석이 가능해지는 것일까? 그 이유는 DFT 연산이 $[-\pi, \pi)$ 범위 내에서 등간격으로 샘플링 된 $N$개의 점들(디지털 각주파수)에 대하여 이루어지기 때문이다.

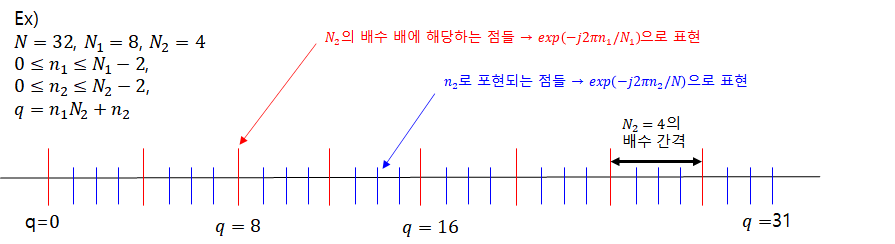
위 그림의 예시에서 보이는 것처럼 모든 N개의 포인트들의 인덱스는 $n_1N2+n_2$의 조합으로 표현될 수 있다. 사실 매우 단순한 논리이다. 우리는 이미 코딩을 할 때, 이중 루프를 돌면서 어떠한 인덱스를 계산할 때 이미 이러한 방식을 무수히도 많이 사용해왔다. 예를 들면, 아래와 같은 인덱스 계산 과정과 근본적으로 다를게 없는 것이다. 모든 것이 그러하듯 알고보면 별 거 아니다.

int i, j, idx;
for (i=0; i<N; i++)
{
	for (j=0;j<M;n++)
    {
		idx = i*M + j;
      	.
      	.
      	.
    }
}

예제 코드

다음은 partial FFT를 사용을 위한 예제코드이다. 내가 사용하는 코드와는 루프를 도는 방식이 조금 다르긴한데 대강 이정도로 코드를 구성할 수 있을 것이다. 다른 언어를 사용하지 않고 C 예제 코드를 남겨 놓는 이유는 다른 언어를 사용할 경우에는 메모리의 여유가 충분한 경우가 많고, Python, MATLAB, R, Julia 등 알고리즘 개발이나 데이터 분석에 사용하는 언어들의 루프 연산 속도가 빠르지 않기 때문에 그냥 행렬 연산을 바로 하는 것이 인덱스를 계산하기 위해 루프를 도는 것보다 빠르기 때문이다. 참고로 아래 코드는 이 포스팅에 간단히 남길 목적으로 방금 대충 짠 것이다. 컴파일도 해보지 않았기 때문에 오류가 발생할 수 있다. 그렇지만 전체적인 뼈대에 이상은 없기 때문에 나중에 참고용으로 사용할 수는 있을 것이다.

#include <stdio.h>
#include <stdint.h>
#include <math.h>

#define N1 16
#define N2 16
#define N  (N1*N2) 
#define PI 3.1415926535897932

typedef struct cplxFloat_
{
    float real;
    float imag;
} cplxFloat;


/* get parial FFT weight vector */
void getWeight(cplxFloat *w, int16_t M, int16_t N)
{
    int16_t i;
    for (i = 0; i < M; i++)
    {
        w[i].real =  cos(2*PI*i/N);
        w[i].imag = -sin(2*PI*i/N);
    }
}

/* complex-valued multiplication */
cplxFloat cplxMul(cplxFloat x, cplxFloat y)
{
    cplxFloat z;

    z.real = x.real*y.real - x.imag*y.imag;
    z.imag = x.real*y.imag + x.imag*y.real;

    return z;
}


int main(void)
{   
    int16_t n, k, n1, n2, p, q, nk;
    int16_t freqMinIdx, freqMaxIdx;
    cplxFloat weight, temp;
    cplxFloat partialFFTout;

    /* 40 ~ 70 번째 주파수 인덱스를 관찰하겠다. */
    specMinIdx = 40;
    specMaxIdx = 70;         

    cplxFloat wCoarse[N1];
    cplxFloat wFine[N2];
    getWeight(wCoarse, (int16_t)N1, (int16_t)N1);
    getWeight(wFine, (int16_t)N2, (int16_t)N);

    /* loop w.r.t. frequency index */
    for (k = freqMinIdx; k <= freqMaxIdx; k++)
    {
        /* loop w.r.t. input sample index */
        partialFFTout.real = partialFFTout.imag = 0;
        for (n = 0; n < N; n++)
        {
            nk = n*k;
            p = nk/N;
            q = nk - p*N;

            n1 = q/N2;
            n2 = q - n1*N2;

            /* w^{kn} in DFT matrix */
            weight = cplxMul(wCoarse[n1], wFine[n2]);

            /* partial FFT output */
            temp = cplxMul(weight, x[n]); // x가 있다고 가정
            partialFFTout.real += temp.real;
            partialFFTout.imag += temp.imag;
        }
        /* 
        partialFFTout 어딘가에 복사 혹은 배열로 잡으면 됨. 이하 생략
        */
    }

    return 0;
}

아래의 코드는 위 코드와 인덱스 계산 방식은 다르지만 결과는 동일하다.

#include <stdio.h>
#include <stdint.h>
#include <math.h>

#define N1 16
#define N2 16
#define N  (N1*N2) 
#define PI 3.1415926535897932

typedef struct cplxFloat_
{
    float real;
    float imag;
} cplxFloat;


/* get parial FFT weight vector */
void getWeight(cplxFloat *w, int16_t M, int16_t N)
{
    int16_t i;
    for (i = 0; i < M; i++)
    {
        w[i].real =  cos(2*PI*i/N);
        w[i].imag = -sin(2*PI*i/N);
    }
}

/* complex-valued multiplication */
cplxFloat cplxMul(cplxFloat x, cplxFloat y)
{
    cplxFloat z;

    z.real = x.real*y.real - x.imag*y.imag;
    z.imag = x.real*y.imag + x.imag*y.real;

    return z;
}


int main(void)
{   
    int16_t n, k, n1, n2;
    int16_t freqMinIdx, freqMaxIdx;
    int16_t coarseFreqIdx, fineFreqIdx;
    int16_t coarseIdxMask = N1-1;
    int16_t fineIdxMask = N2-1;
    cplxFloat weight, temp;
    cplxFloat partialFFTout;

    /* 40 ~ 70 번째 주파수 인덱스를 관찰하겠다. */
    specMinIdx = 40;
    specMaxIdx = 70;         

    cplxFloat wCoarse[N1];
    cplxFloat wFine[N2];
    getWeight(wCoarse, (int16_t)N1, (int16_t)N1);
    getWeight(wFine, (int16_t)N2, (int16_t)N);

    /* loop w.r.t. frequency index */
    for (k = freqMinIdx; k <= freqMaxIdx; k++)
    {
        coarseFreqIdx = (int16_t)(k/N2); 
        fineFreqIdx = k - coarseFreqIdx*N2; 

        /* loop w.r.t. input sample index */
        partialFFTout.real = partialFFTout.imag = 0;
        for (n = 0; n < N; n++)
        {   
            n2 = n*fineFreqIdx;         
            n1 = n*coarseFreqIdx + n2/N2;

            /* bit mask for modulo operation */    
            n1 &= coaseIdxMask;
            n2 &= fineIdxMask;

            /* w^{kn} in DFT matrix */
            weight = cplxMul(wCoarse[n1], wFine[n2]);

            /* partial FFT output */
            temp = cplxMul(weight, x[n]); // x가 있다고 가정
            partialFFTout.real += temp.real;
            partialFFTout.imag += temp.imag;
        }
        /* 
        partialFFTout 어딘가에 복사 혹은 배열로 잡으면 됨. 이하 생략
        */
    }

    return 0;
}

위 두 코드의 차이점은 다음과 같다.

• 첫 번째 코드는 앞에서 살펴본 수식 그대로 구현한 것이다. 즉., DFT matrix의 row index와 column index의 곱은 $nk=pN+q$이고, $q=n_1N_2+n_2$의 관계를 이용하여 $n_1$과 $n_2$를 구한다.
• 반면, 두 번째 코드는 주파수 인덱스를 $k=k_{coarse}N_2+k_{fine}$과 같이 $N_2$의 정수배와 소수배로 분해한 후, $nk=n(k_{coarse}N_2+k_{fine})$과 같이 나타낸 것이다. 우리의 관심 사항은 $n_1$과 $n_2$를 찾는 것이기 때문에 $nk$를 $N_2$로 나누어 $N_2$배의 정수배와 소수배를 표현하면 다음과 같다.
  $nk/N_2 = \underbrace{nk_{coarse} + \lfloor nk_{fine} \rfloor}_{N_2의 정수배} + \underbrace{k_{fine}^{\prime}}_{N_2의 소수배}$
• 위 식에서 두 번째 항인 $N_2$의 소수배는 변수가 int type이기 때문에 0이 되므로, 두 번째 코드와 같이 $n_1$을 구할 수 있다. 반면, $n_2$는 $k_{fine}$이 $N_2$보다 작기 때문에 $nk_{fine}$으로 바로 구하게 된다. 마지막으로 유효 범위 내에서 $n_1$과 $n_2$를 구하기 위해 bit mask를 적용한다.

다차원으로의 확장

지금까지는 1차원 FFT를 기반으로 Partial FFT의 계수 값 계산에 대하여 살펴보았다. 2차원 이상의 partial FFT를 수행할 경우에도 위와같은 원리는 그대로 동작한다. N차원 FFT를 수행할 때, 차원 간 직교성을 만족하기 때문에 인덱스 $q$ 역시 각 차원에 대하여 독립적으로 계산해주면 된다. 코드가 있기는 하지만 앞의 예제 코드를 단순 확장한 것이기 때문에 포스팅은 생략한다.

요약

• 일부 주파수 영역의 신호에만 관심이 있는 경우, parital FFT를 사용할 수 있다.
• partial FFT를 위해서는 식 (1)의 DFT matrix를 이용하여 DFT를 수행하여야 한다.
• DFT matrix 내 포함된 $N^2$개의 계수를 모두 저장하려면 많은 메모리 용량이 필요하므로 L3 메모리에 값들을 저장하고 반복 접근하여야 하는데 이는 프로세싱 속도를 심각하게 떨어뜨린다.
• DFT matrix의 $k$번째 행과 $n$번째 열은 식 (4)와 같이 $N$개의 계수 값만으로도 표현할 수 있는데, 식 (4)를 식 (7)과 같이 다시 분해할 수 있으므로, DFT matrix의 모든 계수 값들은 식 (8)과 같이 $N_1+N_2$개의 계수 값만을 저장하고 이를 이용하여 만들 수 있다.
• 이와 같은 원리는 다차원 FFT에도 그대로 적용할 수 있다.